射線與空間內三角形的相交檢測算法（Möller-Trumbore）的推導與實踐

背景介紹(學習算法之前需要先了解)

射線與空間內三角形的相交檢測是游戲程序設計中一個常見的問題，最典型的應用就是拾取(Picking)，本文介紹一個最常見的方法，這個方法也是DirectX中采用的方法，該方法速度快，而且存儲空間少。先講述理論，然后文章末尾給出對應的代碼實現與Unity中的顯示。
簡單而直觀的方法是：先判斷射線是否與三角形所在的平面相交，如果相交，再判斷交點是否在三角形內。但這種方法效率並不高，因為多計算了三角形所在的平面。
Möller-Trumbore射線三角相交算法是一種快速計算射線與空間內三角形的交點的方法，通過向量與矩陣計算可以快速得出交點與重心坐標，而無需對包含三角形的平面方程進行預計算。它應用於計算機圖形學中以實現涉及三角形網格的光線跟蹤計算。算法名字是以發明者TomasMöller和Ben Trumbore的名字來命名的。

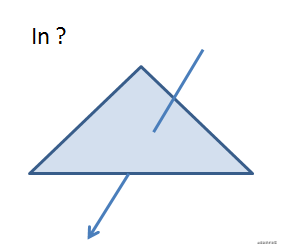
參數說明

設射線的方程Ray=O+td(O為起點，D為射線方向(方向向量)，t為權重)，一個點從起點O開始，沿着方向D移動任意長度，得到終點R，根據t值得不同，得到得R值也不同，所有這些不同的R值便構成了整條射線。
三角形三個頂點\(P0\)，\(P1\)，\(P2\)。\(u\)為\(P_1\)的權重，\(v\)為\(P_2\)的權重，而\(1-u-v\)是\(P_0\)的權重，可以理解為沿着邊AC移動一段距離，然后再沿着邊AB移動一段距離，最后求它們的和向量。至於移動多大距離，就是由參數u和v控制的，所表達的數學意義是三角形及其內部所有點的方程。

\[Ray:O+td{\quad}(t≥0) \]

\[(1-u-v)P0+uP1+vP2 \]

推導過程

兩個重要的定理

克萊姆法則

解線性方程組時

\[\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]\left[ \begin{matrix} t \\ u \\ v\end{matrix} \right]=S \]

D，E1，E2是含有三個參數的行列式，即可表達成

\[ t=\frac{det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}=\frac{\left[ \begin{matrix} S_x & E_{x1} & E_{x2} \\ S_y & E_{y1} & E_{y2} \\ S_{z} & E_{z1} & E_{z2}\end{matrix} \right]}{\left[ \begin{matrix} -D_x & E_{x1} & E_{x2} \\ -D_y & E_{y1} & E_{y2} \\ -D_{z} & E_{z1} & E_{z2}\end{matrix} \right]} \]

\[ u=\frac{det{\left[ \begin{matrix} -D & S & E_2\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}=\frac{\left[ \begin{matrix} -D_x & S_x & E_{x2} \\ -D_y & S_y & E_{y2} \\ -D_{z} & S_z & E_{z2}\end{matrix} \right]}{\left[ \begin{matrix} -D_x & E_{x1} & E_{x2} \\ -D_y & E_{y1} & E_{y2} \\ -D_{z} & E_{z1} & E_{z2}\end{matrix} \right]} \]

\[ v=\frac{det{\left[ \begin{matrix} -D & E_1 & S\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}=\frac{\left[ \begin{matrix} -D_x & E_{x1} & S_{x} \\ -D_y & E_{y1} & S_y \\ -D_{z} & E_{z1} & S_z\end{matrix} \right]}{\left[ \begin{matrix} -D_x & E_{x1} & E_{x2} \\ -D_y & E_{y1} & E_{y2} \\ -D_{z} & E_{z1} & E_{z2}\end{matrix} \right]} \]

向量混合積

\[ a·(b×c)=b·(c×a)=c·(a×b)\\ a·(b×c)=-a·(c×b)\\ a·(b×c)=-b·(a×c)\\ a·(b×c)=-c·(b×a) \]

將方程聯立

\[O+td=(1-u-v)P0+P1+P2{\quad}(u≥0,v≥0,u+v≤1) \]

化簡

\[O-P0=u(P1-P0)+v(P2-P0)-td\\ S=uE_1+vE_2-td\\{\quad}(S=O-P0,E_1=P1-P0,E_2=P2-P0) \]

\[\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]\left[ \begin{matrix} t \\ u \\ v\end{matrix} \right]=S \]

克拉姆法則

\[t=\frac{det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}} \]

向量混合積
分母部分
運用向量混合積定理，D前的-號，被抵消了

\[ det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}=-D·(E_1×E_2)=E_1·(D×E_2) \]

令

\[ S1=D×E_2 \]

分子部分：

\[ det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}=((S×E_1)·E_2) \]

令

\[ S2=S×E_1 \]

原式等於

\[ det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}=S2·E_2 \]

因此

\[ t=\frac{S2·E_2}{E_1·S1} \]

同理可推得其他兩個參數u，v

\[ u=\frac{S1·S}{E_1·S1} \]

\[ v=\frac{S2·D}{E_1·S1} \]

總結

我們在最后可以通過已知的數據，求出t、u、v三個參數，通過三個參數的范圍限制判斷是否相交，如果不滿足則不相交，如果滿足則相交

代碼實現

    // Vector3 a b c triangle vertexs
    // orig is ray original point, dir is direction vector
    bool rayTriangleIntersect(Vector3 orig, Vector3 dir,
        Vector3 a, Vector3 b, Vector3 c, float t, float b1, float b2)
    {
        bool isIn = false;
        Vector3 E1 = b - a;
        Vector3 E2 = c - a;
        Vector3 S = orig - a;
        Vector3 S1 = Vector3.Cross(dir, E2);
        Vector3 S2 = Vector3.Cross(S, E1);

        // 共同系數
        float coeff = 1.0f / Vector3.Dot(S1, E1);
        t = coeff * Vector3.Dot(S2, E2);
        b1 = coeff * Vector3.Dot(S1, S);
        b2 = coeff * Vector3.Dot(S2, dir);

        Debug.Log($"t = {t}, b1 = {b1}, b2 = {b2}");

        if (t >= 0 && b1 >= 0 && b2 >= 0 && (1 - b1 - b2) >= 0)
        {
            isIn = true;
        }

        return isIn;
    }

Unity中的演示效果

當射線與三角形相交時，三角形的材質會變成紅色，射線是采用LineRenderer的形式，三角形用了編輯材質頂點的腳本，過幾天會分享出來~
項目地址:https://github.com/shadow-lr/RayTriangleIntersect

題外話

雖然射線和三角形的相交檢測可以用來實現拾取(Picking)，但是大多數程序並不采用這個方法，原因是這個方法效率很低，我們可以設想，一個大型的3D游戲，某個模型的三角形數量很可能是百萬級的，在此情況下，對模型上的每個三角形求交是一件極其耗費時間的事情。
所以一般可行的方法是，用包圍球和包圍盒（AABB、OBB、FDH）來代替，計算出能容納模型的最小球體或者舉行提，只要判斷射線與包圍球或者包圍盒求交即可，只是精確度上有一定誤差，但是足以滿足多數程序的需要。