【統計學】6.統計量及其抽樣分布

【統計學】6.統計量及其抽樣分布

6.1 統計量

6.2 抽樣分布

6.3 樣本均值的分布與中心極限定理

6.4 由正態分布導出的幾個重要分布

學習目標

1.了解統計量及其分布的幾個概念

2.了解由正態分布導出的幾個重要分布

3.理解樣本均值的分布與中心極限定理

4.掌握單樣本比例和樣本方差的抽樣分布

6.1 統計量

6.1.1 統計量的概念

統計量（statistic）

1. 設

\[X_1,X_2,...,X_n \]

是從總體X中抽取的容量為n的一個樣本，如果由次樣本構造一個函數

\[T(X_1,X_2,...,X_n) \]

不依賴於任何未知參數，則稱函數

\[T(X_1,X_2,...,X_n) \]

是一個統計量

樣本均值、樣本比例、樣本方差等都是統計量

2. 統計量是樣本的一個函數
3. 統計量是統計推斷的基礎

6.1.2 常用統計量

(1)樣本均值

\[\overline X = \frac{1}{n}\sum^n_{i=1}X_i \]

(2)樣本方差

\[S^2 = \frac{1}{n-1}\sum^n_{i=1}(X_i-\overline X)^2 \]

(3)樣本變異系數

\[V = S \sqrt{X} \]

(4)k階矩

\[m_k = \frac{1}{n}\sum^n_{i=1}X^k_i \]

(5)k階中心矩

\[v_k = \frac{1}{n-1}\sum^n_{i=1}(X_i-\overline X)^k \]

(6)樣本偏度

\[\alpha_3 =\frac{ \sqrt{n-1}\sum^n_{i=1}(X_i-\overline X)^3}{\sum^n_{i=1}(X_i-\overline X)^{\frac{3}{2}}} \]

(7)樣本峰度

\[\alpha_4 = \frac{n-1\sum^n_{i=1}(X_i-\overline X)^4}{[\sum^n_{i=1}(X_i-\overline X)^2]^2}-3 \]

6.2 抽樣分布（sampling distribution）

1. 樣本統計量的概率分布，是一種理論分布
   1. 在重復選取容量為n的樣本時，由該統計量的所有可能取值形成的相對頻數分布
2. 隨機變量是樣本統計量
   1. 樣本均值、樣本比例、樣本方差等
3. 結果來自容量相同的所有可能樣本
4. 提供了樣本統計量長遠而穩定的信息，是進行推斷的理論基礎，也是抽樣推斷科學性的重要依據

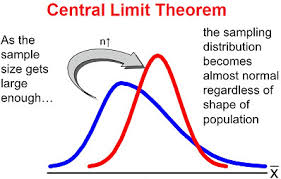
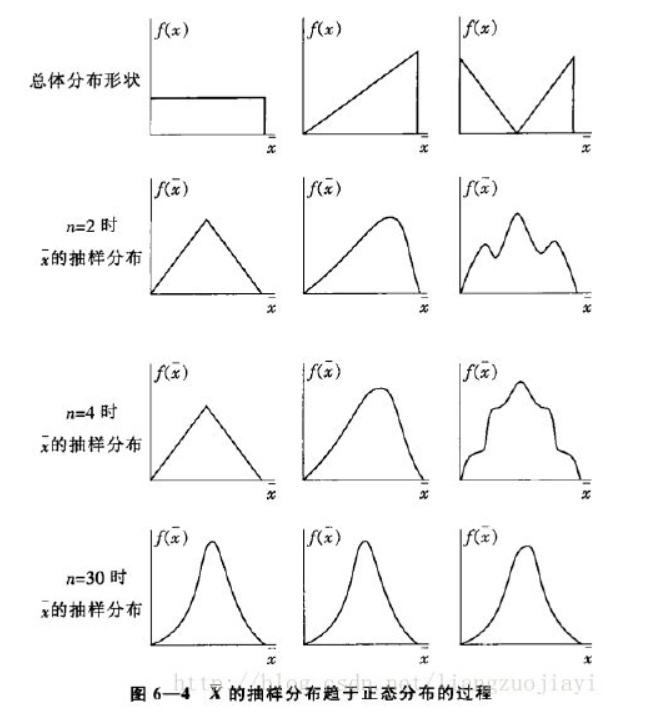
6.3 樣本均值的分布與中心極限定理

樣本均值的抽樣分布

1. 在重復容量為n的樣本時，由樣本均值的多有可能取值形成的相對頻數分布
2. 一種概率分布
3. 推斷總體均值μ的理論基礎

當總體服從正態分布

\[N(\mu,\sigma^2) \]

來自該總體的所有容量為n的樣本的均值

\[\overline x \]

也服從正態分布，

\[\overline x \]

的數學期望為

\[\mu \]

方差為

\[\frac{\sigma^2}{n} \]

即

\[\overline x \backsim N(\mu,\frac{\sigma^2}{n}) \]

中心極限定理(central limit theorem)

從均值為μ，方差為

\[\sigma^2 \]

的任意一個總體中抽取容量為n的樣本，當n充分大時，樣本均值的抽樣分布近似服從均值為μ，方差為

\[\frac{\sigma^2}{n} \]

的正態分布

6.4 由正態分布推導出來的幾個重要分布

卡方分布

1. 有阿貝(Abbe)於1863年首先給出，后來由海爾墨特(Hermert)和卡·皮爾遜(K·Person)分別於1875年和1900年推導出來

2. 設

   \[X \backsim N(\mu,\sigma^2) \]

   則

   \[z = \frac{X-\mu}{\sigma} \backsim N(0,1) \]

3. 令

   \[Y = z^2 \]

   則Y服從自由度為1的卡方分布，即

   \[Y \backsim \chi^2(1) \]

4. 當總體

   \[X \backsim N(\mu,\sigma^2) \]

   從中抽取容量為n的樣本，則

   \[\frac{\sum^2_{i=1}(x_i-\overline x)^2}{\sigma^2} \backsim \chi^2(n-1) \]

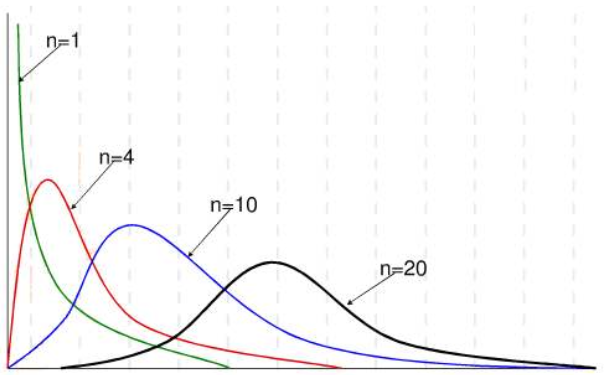
卡方分布的性質和特點

1. 分布的變量始終為正
2. 分布的形狀取決於其自由度n的大小，通常為不對稱的正偏分布，但隨着自由度的增大逐漸趨於對稱
3. 期望為

\[E(\chi^2) = n \]

方差為

\[D(\chi^2) = 2n \]

其中n為自由度

4. 可加性：若U和v為兩個獨立的卡方分布隨機變量，

\[U \backsim \chi^2(n_1),V \backsim \chi^2(n_2) \]

則

\[U+V \]

這一隨機變量服從自由度為

\[n_1+n_2 \]

的卡方分布

t分布

1. 高賽特(W.S.Gosset)於1908年在一篇以"student"為筆名的論文中首次提出
2. t 分布式類似正態分布的一種對稱分布，它通常要比正態分布平坦和分散
3. 一個特定的分布依賴於稱之為自由度的參數。隨着自由度的增大，分布也逐漸趨於正態分布

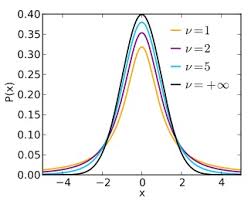
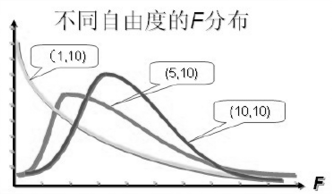
F分布

1. 由統計學家費希爾（R.A.Fisher）提出的，以其姓氏的第一個字母來命名

2. 設若U為服從自由度為n1的卡方分布，即

   \[U \backsim \chi^2(n_1) \]

   V為服從自由度為n2的卡方分布，即

   \[V \backsim \chi^2(n_2) \]

   且U和V相互獨立，則稱F為服從自由度n1和n2的F分布，記為

   \[F = \frac{\frac{U}{n_1}}{\frac{V}{n_2}} \]
   \[F \backsim F(n_1,n_2) \]

   

例題

例題 1

設從一個均值μ=10，標准差sigma=0.6的總體中隨機選取容量n=36的樣本。假定該總體不是很偏，要求：

1. 樣本均值小於9.9的近似概率

   n=36說明是大樣本，則該樣本均值是滿足

   \[\overline x \backsim N(10,\frac{0.6^2}{36}) = N(\mu,\sigma^2) \\ \mu = 10 ,\sigma = 0.1 \]

   先進行標准化

   \[P(\overline x <9.9) = P(\frac{\overline x -10}{0.1}<\frac{9.9-10}{0.1}) \\ \phi(-1) = 1- \phi(1) = 1-0.8413 = 0.1587 \]

2. 樣本均值超過9.9的近似概率

\[P(\overline x >9.9) = P(Z>-1) = \phi(1) = 0.8413 \]

3. 樣本均值在總體均值10附近0.1范圍的概率

\[P(9.9< \overline x <10.1) = P(-1<Z<1) = 2\phi(1) -1 = 0.6826 \]

例題2

某汽車電瓶生產商稱其生產的電瓶均有均值為60個月，標准差為6個月的壽命分布。現假設質檢部門決定檢驗該廠的說法是否正確，為此隨機抽取了50個該廠生產的電瓶進行壽命試驗

1. 假定廠方聲稱是正確的，試描述50個電瓶的平均壽命的抽樣分布

   \[\overline X \backsim N(60,\frac{36}{50}) \]

2. 假定廠方聲稱是正確的，試描述50個樣本組成的樣本的平均壽命不超過57個月的概率

\[P(\overline X \leq 57) = P(\frac{\overline X -60}{\sqrt{0.72} }\leq \frac{57-60}{\sqrt{0.72}}) \\= 1 - \phi(3.529) = 1-0.9998 = 0.0002 \]

例題3

\[Z_1,Z_2,...Z_6 \]

表示從標准正態總體中隨機抽取的容量為n=6的一個樣本，試確定常數b，使得，

\[P(\sum^6_{i=1}Z^2_i \leq b) = 0.95 \]

這是一個小樣本，總體服從正態分布則

\[Z_i \backsim N(0,1) \]

\[P(\chi^2_{6} \leq b) = 0.95 \\ P(\chi^2_{6} > b) = 0.05 \\ b = 12.592 \]