判斷點在多邊形內算法（凸多邊形和復雜多邊形）

判斷點是否在凸多邊形內

• 這個判斷比較的簡單，只需要按一定順序遍歷三角形頂點，與紅點進行連線，按照順時針或逆時針進行叉乘

	bool PointIsInPolygon()
    {
        int j = points.Length - 1;

        bool oddNodes = false;

        for (int i = 0; i < points.Length; ++i)
        {
            // y1 < y && y >= y2
            // y2 < y && y >= y1
            float z = testPoint.position.z;
            float z1 = points[i].position.z;
            float z2 = points[j].position.z;

            float x = testPoint.position.x;
            float x1 = points[i].position.x;
            float x2 = points[j].position.x;

            // 向量PC
            float difXPC = x2 - x;
            float difZPC = z2 - z;

            // 向量PA
            float difXPA = x1 - x;
            float difZPA = z1 - z;

            float crossResult = difXPC * difZPA - difZPC * difXPA;

            if (i == 0)
            {
                oddNodes = (crossResult >= 0) ? true : false;
            }

            bool cross = (crossResult >= 0) ? true : false;

            if (cross != oddNodes)
            {
                return false;
            }
            j = i;
        }

        return true;
    }

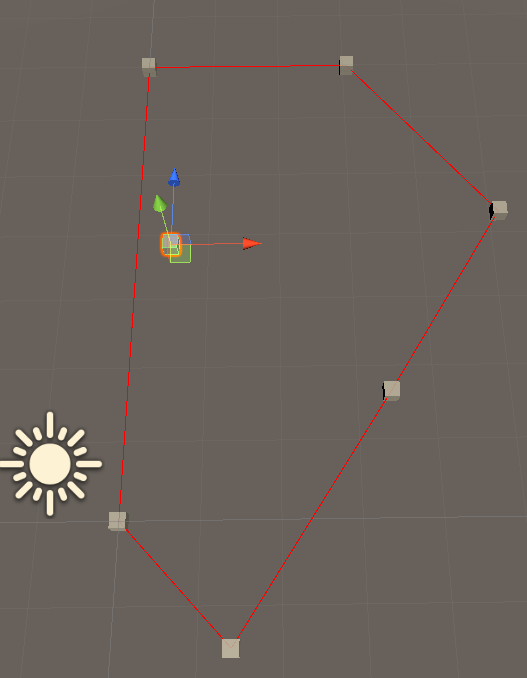
判斷點是否在任意多邊形內

判斷流程：

• 隨便選取多邊形邊上的一點（comparePoint），並且與判斷的點形成射線（originPoint射向comparePoint）
• 判斷兩個線段是否相交，通過兩次叉乘的形式，分別計算是否在不同側

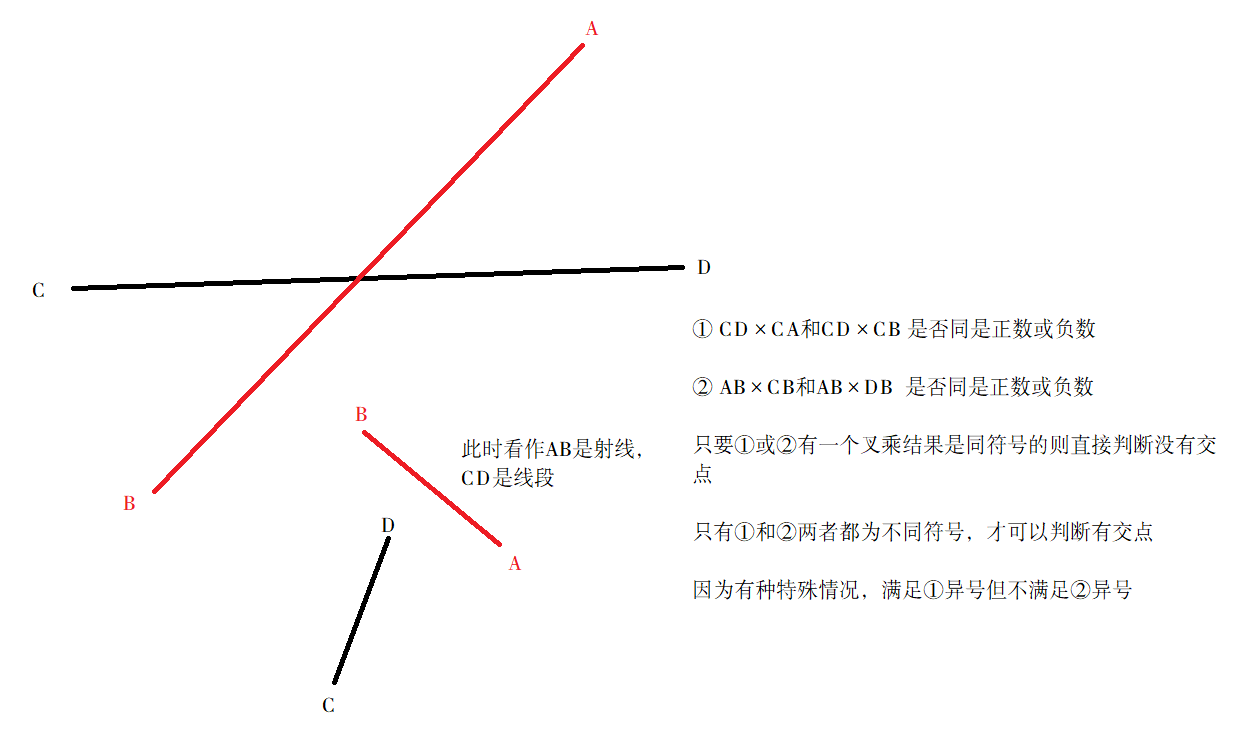
• 遍歷多邊形的每個邊，計算邊與之相交的次數，如果是奇數就在多邊形內，否則則在多邊形外

	// 主函數中判斷點是否在任意三角形內
	if (CheckPointIsInPolygon())
    {
		Debug.Log("Point is in Polygon");
		drawColor = Color.red;
	}
	else
	{
		drawColor = Color.white;
	}    
	bool CheckPointIsInPolygon()
    {
        if (points.Length < 3)
        {
            return false;
        }

        float raycastLen = 10000f;
        Vector3 comparePoint = (points[0].position + points[1].position) * 0.5f;
        // 此處一定要這樣寫表示射線，不然comparePoint在邊上計算會有誤差
        comparePoint += (comparePoint - testPoint.position).normalized * raycastLen;
        Gizmos.DrawLine(testPoint.position, comparePoint);

        int count = 0;

        for (int i = 0; i < points.Length; ++i)
        {
            Vector3 a = points[i].position;
            Vector3 b = points[(i + 1) % points.Length].position;
            
            // 循環判斷每條邊與testPoint射向comparePoint的射線是否有交點
            if (IsIntersection(a, b, testPoint.position, comparePoint))
            {
                ++count;
            }
        }

        if (count % 2 == 1) return true;

        return false;
    }

    bool IsIntersection(Vector3 a, Vector3 b, Vector3 originPoint, Vector3 comparePoint)
    {
            // 判斷是否同向
            float crossA = Mathf.Sign(Vector3.Cross(comparePoint - originPoint, a - originPoint).y);
            float crossB = Mathf.Sign(Vector3.Cross(comparePoint - originPoint, b - originPoint).y);

            if (Mathf.Approximately(crossA, crossB)) return false;

            float crossC = Mathf.Sign(Vector3.Cross(b - a, originPoint - a).y);
            float crossD = Mathf.Sign(Vector3.Cross(b - a, comparePoint - a).y);

            if (Mathf.Approximately(crossC, crossD)) return false;

            return true;
    }

特殊情況

• 剛好在點上或者在線上。實際運用時會有誤差，但不影響

參考博文

點在多邊形內算法——判斷一個點是否在一個復雜多邊形的內部：https://blog.csdn.net/hjh2005/article/details/9246967

2D空間中求一點是否在多邊形內：https://www.cnblogs.com/hont/p/6105997.html)https://www.cnblogs.com/dabiaoge/p/4491540.html