圖像復原與重建
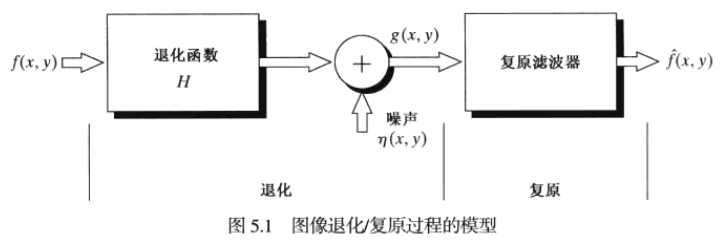
圖像退化/復原過程模型
空域退化過程
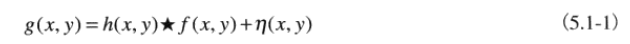
頻域退化過程
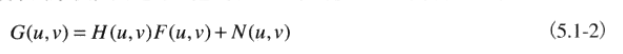
退化與復原基本原理
噪聲模型
噪聲的空間域頻率特性
白噪聲——傅里葉譜是常量的噪聲。
一些重要的噪聲概率密度函數
高斯噪聲、瑞利噪聲、伽馬噪聲、指數噪聲、均勻噪聲、椒鹽(脈沖)噪聲、
噪聲圖像及其直方圖
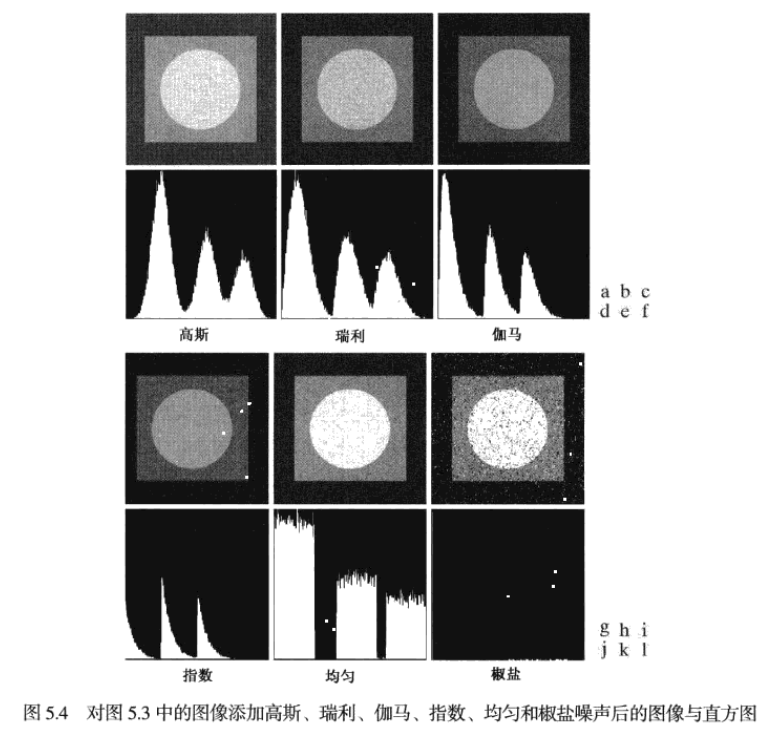
由脈沖噪聲污染的圖像的椒鹽招生的外觀是唯一一種引起退化、視覺上可區分的噪聲類型。
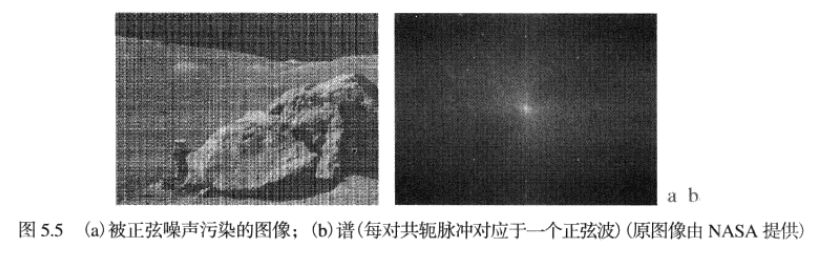
周期噪聲
周期噪聲可通過頻率域濾波來顯著地減少,如果空間域中正弦波的振幅足夠強,我們在改圖像的譜中將看到圖像中每個正弦波的脈沖對。
只存在噪聲的復原——空間濾波
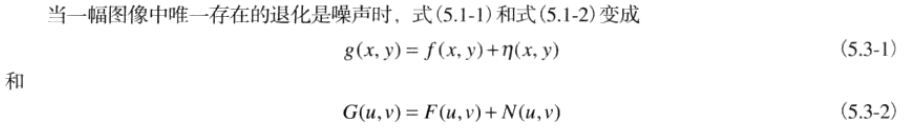
均值濾波器: 算術均值濾波器 、幾何均值濾波器 、諧波均值濾波器、 逆諧波均值濾波器
均值濾波器實例

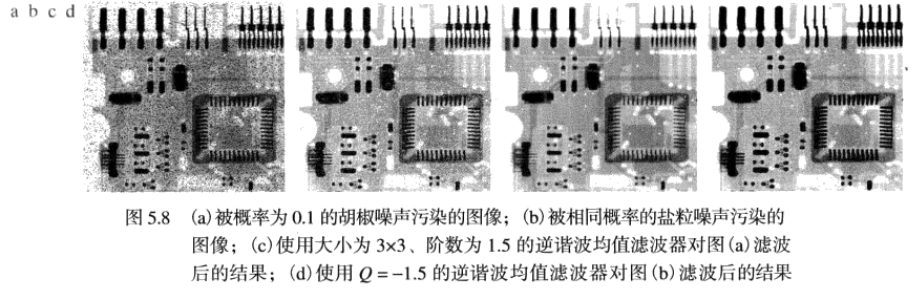
總結:算術均值濾波器和幾何均值濾波器更加適合於處理高斯或者均勻隨機噪聲, 逆諧波均值濾波器更適合於處理脈沖噪聲。 通過明確噪聲是暗噪聲還是亮噪聲,以便於為Q選擇正確的符號。
統計排序濾波器
統計排序濾波器是空間域濾波器,空間濾波器的響應基於由該濾波器包圍的圖像區域中的像素值的順序,排序結果決定濾波器的響應。
主要有:中值濾波器、最大值最小值濾波器、中點濾波器、修正的阿爾法均值濾波器
中值濾波器和修正的阿爾法濾波器針對脈沖噪聲相比算術和幾何均值濾波器有更好的作用。
自適應濾波器
隨機變量最簡單的度量是其均值和方差,均值為區域內平均灰度的度量,方差為該區域的對比度的度量。

自適應中值濾波器
算法過程:

目的:確定中值濾波器的輸出 Zmed 是否是一個脈沖,如果不是脈沖則轉到 B,如果是 則擴大窗口尺寸。
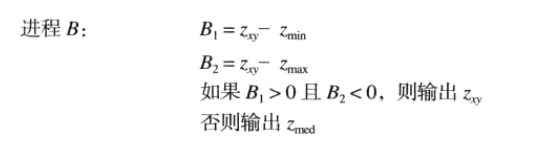
其中:

算法主要作用:(1)去除椒鹽噪聲;(2)平滑其他非脈沖噪聲;(3)減少諸如物體邊界細化或者粗化等失真。
自適應中值濾波實例

(b)中噪聲有被有效消除, 但是導致了圖像細節的損失。
用頻率域濾波消除周期噪聲
帶阻濾波器
應用:在頻率域噪聲分量的一般位置近似已知的應用中消除噪聲。
帶通濾波器
帶通濾波器幫助屏蔽了噪聲模式,簡化了噪聲分析,與圖像內容無關。
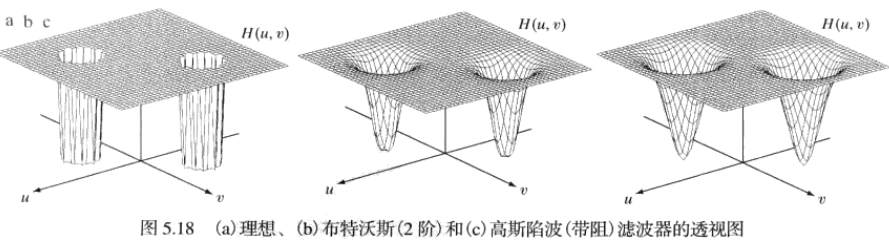
陷波濾波器
陷波濾波器阻止事先定義的中心頻率的鄰域內的頻率。
由於傅里葉變換的對稱性,要獲得有效的結果,陷波濾波器必須以關於原點對稱的形式出現。
最佳陷波濾波
解決多種干擾分量,在濾波可以避免消除太多的圖像信息。
線性、位置不變的退化


以上表明,具有加性噪聲的線性空間不變退化系統,可在空間域建模為退化(點擴散)函數與一幅圖像的卷積,然后再加上噪聲。

估計退化函數
方法: 觀察法、試驗法、數學建模法。使用以某種方式估計的退化函數來復原一幅圖像的過程,稱為盲去卷積過程,因為真正的退化函數很少能完全知曉。
圖像觀察估計

試驗估計
使用相同系統的對一個沖激(小亮點)成像,得到退化的沖激響應。

建模估計
例:基於大氣湍流的物理特性引起的退化模型。

逆濾波
解決退化函數為0或者非常小的值的問題是一種方法是限制濾波的頻率,使其接近0點。
最小均方誤差(維納)濾波

最小均方誤差濾波 == 最小二乘誤差濾波
SNR 和 MSE 的定義:

逆濾波和維納濾波的比較


約束最小二乘方濾波
維納濾波存在的困難:為退化圖像和噪聲的功率譜必須是已知的,然而功率比的常數估計並不總是一個合適的解。
將圖像復原問題簡化為簡單的矩陣操作。
維納濾波和最小二乘方濾波的比較

幾何均值濾波
通過參數構造前面提到過的濾波方法。

由投影重建圖像
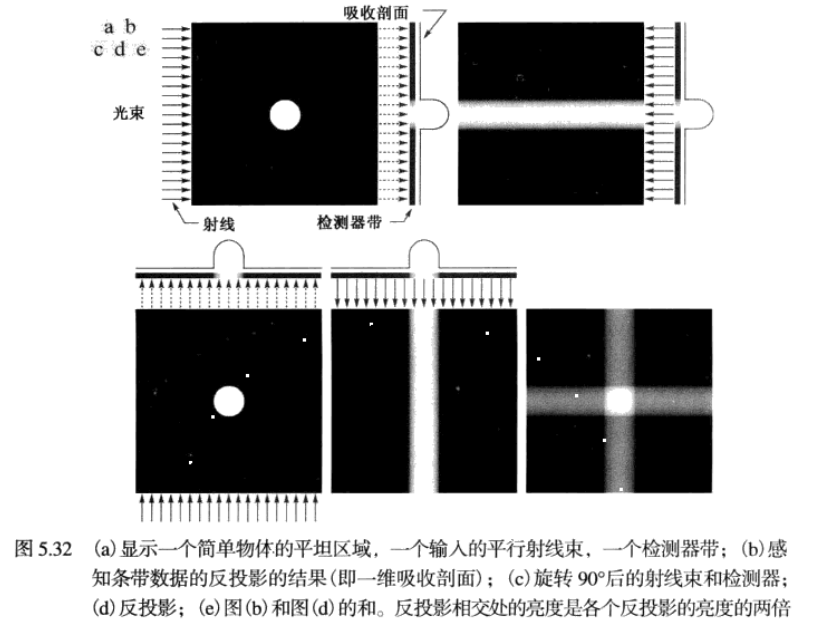
反投影法:沿着射線來的方向將一維信號反投影回去。
反投影重建實例
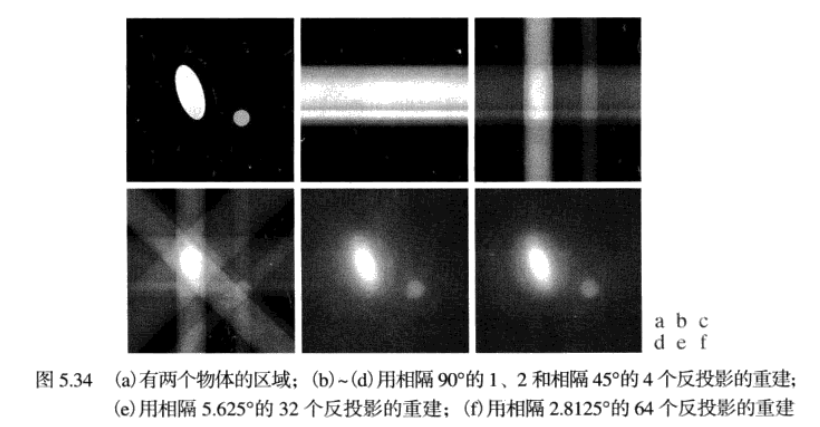
分別使用32個和64個反投影能夠得到更精確的重建,視覺上非常接近,而且兩者都存在模糊問題。
計算機斷層(CT)原理

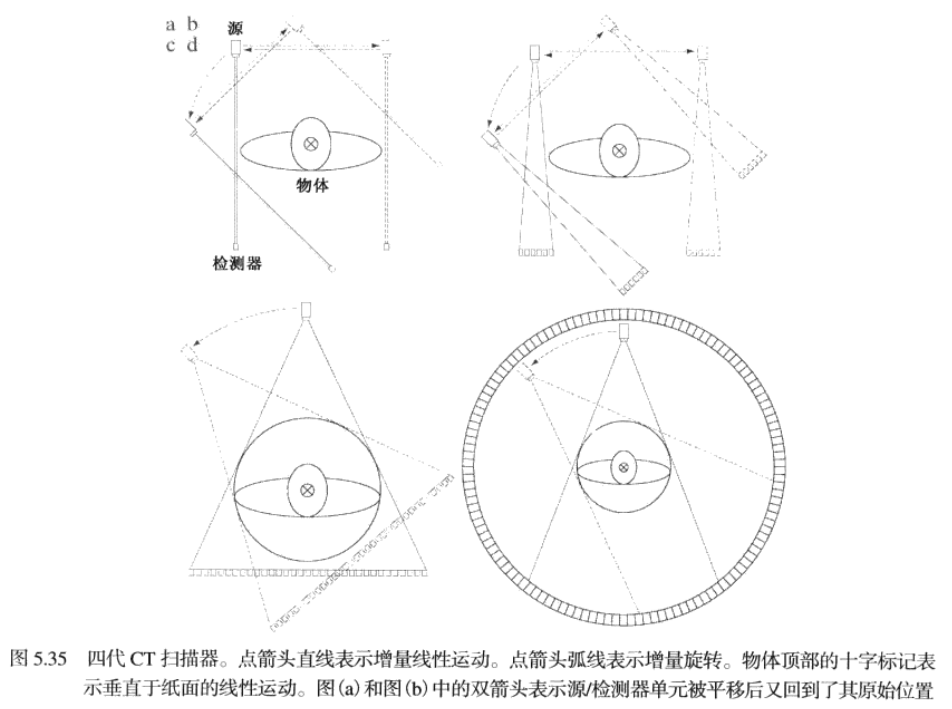
投影和雷登變換

沿着xy 平面中任意一條線的f(x,y)的投影(線積分)的公式為雷登變換。
使用雷登變換得到原型區域的投影實例

正弦圖——雷登變換 關於p 與 theata的圖像。
CT的關鍵目的是 從投影得到物體的三維表示。 方法為反投影每一個投影,然后對反投影求和以產生一幅圖像(切片),堆積所有的結果圖像產生三維物體的再現。
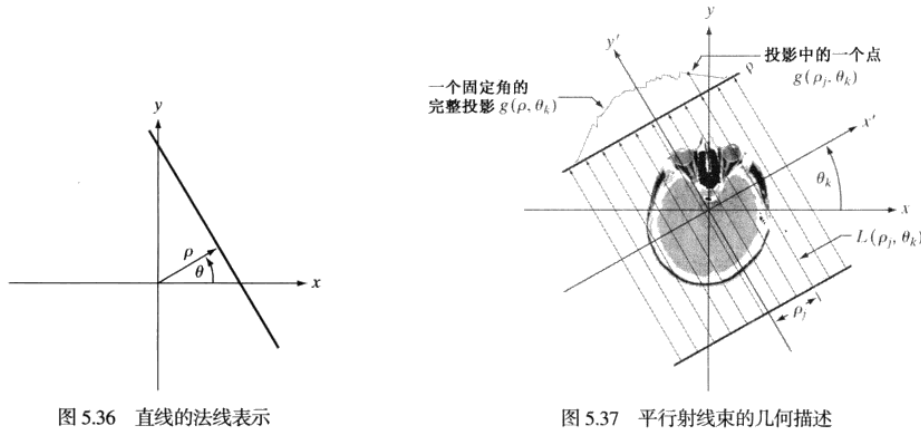
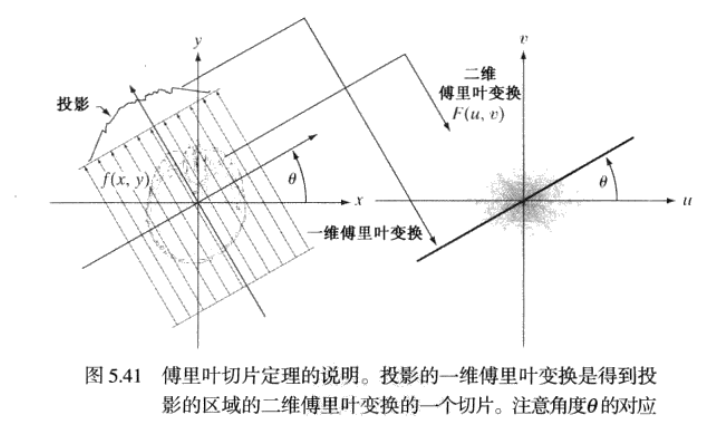
傅里葉切片定理(投影切片定理)
模糊問題的重建方法基礎——投影的一維傅里葉變換和得到投影區域的二維傅里葉變換關系投影p 的一維傅里葉變換
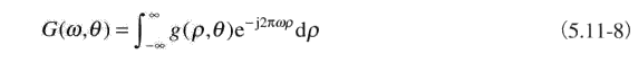
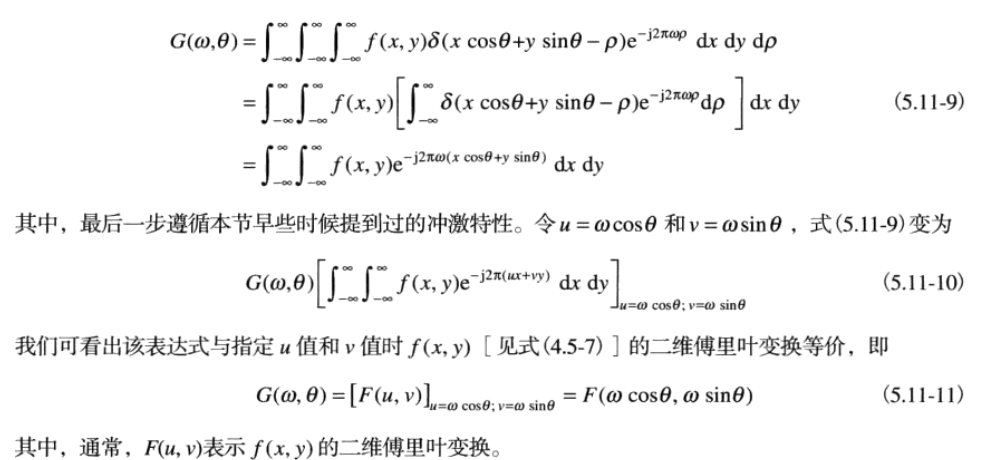
(5.11-11)為傅里葉切片定理(投影切片定理)。
使用平行射線束濾波反投影的重建
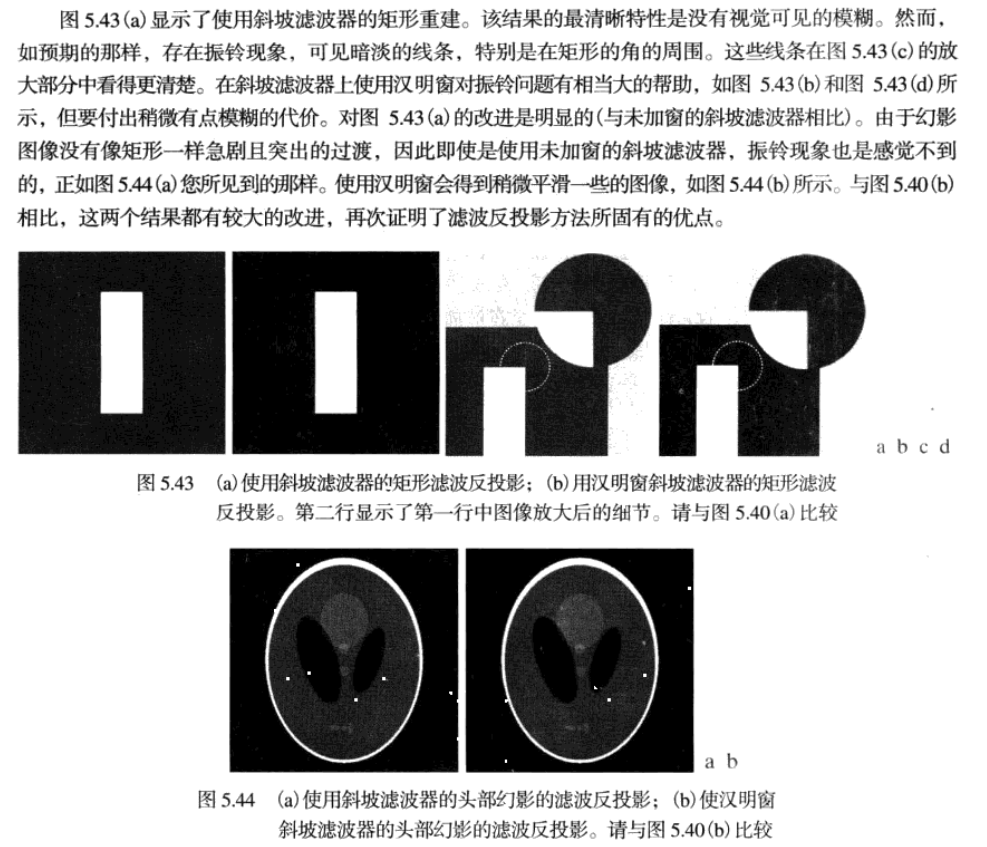
直接得到反投影會生成不可接受的模糊結果,解決方法:在計算反投影之前對投影做簡單的濾波。
使用濾波反投影的圖像重建實例
傅里葉變換在理論表示和算法開發中扮演了重要角色,其中MATLAB中CT圖像處理就是基於FFT的。
使用扇形射線束濾波反投影的重建
以卷積為基礎推導扇形射線濾波反投影