線性時間選擇算法

顧名思義，“線性時間選擇”就是“選擇問題”的“線性時間”算法。

1. 選擇問題

元素選擇問題：給定一個能夠線性排序的集合（該集合中有 n 個元素）和 一個整數 k（\(1 \le k \le n\)） ，找出這 n 個元素中第 k 小的元素。

時間下界：

• 當 \(k = 1 或 k = n\)時，時間復雜度為 \(O(n)\)

• 當 \(k \le n/log(n) 或 k \ge n - n/log(n)時\)，時間復雜度為\(O(n + klog(n)) = O(n)\)（堆排序）

2. 解決方法

方法一：先排序，再找第 k 小的數。至少：\(O(n)\) 平均：\(O(nlog(n))\)時間

方法二：隨機選擇算法：使用快速排序方法, 最多對一段繼續分解 最壞時間\(O(n^2)\), 平均時間\(O(n)\)

1. RamdomizedPartition(a, p, r) 快排中的分解算法

   1. i=Ramdom(p,r) //在p:r中隨機選擇一個數i

   2. 交換 a[i] 與 a[p] //將a[i]換到左端點

   3. 執行Partition(a,p,r)

   RamdomizedPartition(a, p, r)     //排序a[p:r] 
   {     
       i = Ramdom(p, r); 
       swap(a[i], a[p]);
       return Partition(a, p, r);
   }
   

2. RandomSelect(a, p, r)

   RSelect(a,p,r,k)      //選擇a[p:r]中第k小數
   {  
       if (p == r)
           return a[p];
       mid=RamdomizePartition(a, p, r); 
       if( mid >= k)
           return (RSelect(a, p, mid, k)); 
       else 
           return (RSelect(a, mid + 1, r, k - mid);              
   }   //初略時間分析:  T(n) = T(9n/10) + O(n) = O(n)
   

方法三：線性時間選擇算法 Select() ：對快速排序的改進，最壞時間\(O(n)\)。

1. 將 n 個元素，分成\(\lceil n/5 \rceil\)組，取出每組的中位數（第三小的元素）
2. 取出\(\lceil n/5 \rceil\)個中位數的中位數（Select函數可以取中位數）
3. 利用快排中的分解函數 Partition()，以所求中位數為基准，划分 a[p : r] 為兩段。
4. 取其中一段進行遞歸。

template <class Type>
Type Select(Type a[], int p, int r, int k)
{	
    if( r - p < 75 ) 
    { 
        直接對數組a[p:r]排序;  
        return a[p+k-1];
    }
 	for( int i = 0; i <= (r - p - 4) / 5 ; i++ )  	//分 n/5 組, 取各組中位數
    {
		swap(a[p + 5*i]至a[p+5*i+4]的第3小元素, a[p+i]);
    }
    Type x = Select(a, p, p+(r-p-4)/5, (r-p-4)/10); //取中位數的中位數, T(n/5)
	
    int i = Partition(a, p, r, x), j = i - p + 1; 
	
    if ( k == j ) 
        return a[i];
	else if ( k < j ) 
        return Select(a,p,i-1,k);    //選擇左片遞歸, 最多T(3n/4)
	else 
        return Select(a,i+1,r,k-j);  //選擇右片遞歸, 最多T(3n/4)
 }

時間復雜度分析：

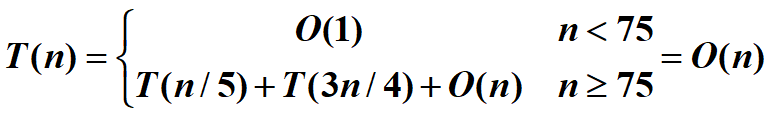
總結：算法優化的歷程

算法	快排	隨機選擇	線性時間選擇
時間復雜度	\(O(nlog(n))\)	\(O(n) -- O(n^2)\)	\(O(n)\)
基准值	a[p]	random	中位數

附：line-time-select.c

#include <stdio.h>
#define MAX 2000010
int num[MAX];
// 選擇排序
void slsort(int p, int q)
{
    for (int i = p + 1; i <= q; i++)
    {
        int temp = num[i], j = i - 1;
        while (j >= p)
        {
            if (num[j] > temp)
            {
                num[j + 1] = num[j];
                j--;
            }
            else
                break;
        }
        num[j + 1] = temp;
    }
}
// 分解函數
int Partition(int p, int q, int mid)
{
    int i = p, j = q;
    while (i <= q && j >= p)
    {
        while (num[i] < mid){i++;}
        while (num[j] > mid){j--;}
        if (i >= j)
            break;
        else
        {
            int temp = num[i];
            num[i] = num[j];
            num[j] = temp;
            i++, j--;
        }
    }
    return j;
}
// 選擇函數
int Select(int p, int q, int k)
{
    if (q - p < 75)
    {
        slsort(p, q);
        return num[p + k - 1];
    }
    // 選出 n/5 組中每個組的中位數
    for (int i = 0; i <= (q - p - 4) / 5; i++)
    {
        slsort(p + 5 * i, p + 5 * i + 4);
        int temp = num[p + 5 * i + 2];
        num[p + 5 * i + 2] = num[p + i];
        num[p + i] = temp;
    }
    // 選出各種中位數的中位數 mid
    int mid = Select(p, p + (q - p - 4) / 5, ((q - p - 4) / 5 + 1) / 2);
    // 以 mid 為基准進行分解
    int mid_id = Partition(p, q, mid);
    int mid_rank = mid_id - p + 1;
    // 遞歸條件判斷
    if (k == mid_rank)
    {
        return num[mid_id];
    }
    else if (k < mid_rank)
    {
        return Select(p, mid_id, k);
    }
    else
    {
        return Select(mid_id + 1, q, k - mid_rank);
    }
}
int main(int argc, char const *argv[])
{
    int i = 0, k;
    while (scanf("%d", &num[i]) != EOF) {i++;}
    scanf("%d", &k); // 選擇第幾小的元素
    if( k > i)
        printf("error!\n");
    else
        print("%d\n", Select(0, i, k));
    return 0;
}