排隊論簡介
歷史
- 排隊論又稱隨機服務系統,是研究系統隨機聚散現象和隨機 服務系統工作過程的數學理論和方法,是運籌學的一個分支。
- 排隊論的基本思想是 1909 年丹麥數學家 A.K. 埃爾朗在解 決自動電話設計問題時開始形成的,當時稱為話務理論。
- 現實生活中如排隊買票、病人排隊就診、輪船進港、高速路 上汽車排隊通過收費站、機器等待修理等都屬於排隊論問題。
定義
- 通過對服務對象到來及服務時間的統計研究
- 得出這些數量指標(等待時間、排隊長度、忙期長短(決定服務台數量)等)的 統計規律,
- 然后根據這些規律來改進服務系統的結構或重新組織被服務 對象
- 使得服務系統既能滿足服務對象的需要,又能使機構的費用 最經濟或某些指標最優。
應用
- CUMCM 2009B 的眼科病床的合理安排問題
- MCM 2005B 收費站最佳配置問題
- ICM 2017D 機場安檢問題
模型與模擬
排隊論基本構成與指標
排隊論的基本構成
- 輸入過程:描述顧客按照怎樣的規律到達排隊系統。顧客總 體(有限/無限)、到達的類型(單個/成批)、到達時間間隔。
- 排隊規則:指顧客按怎樣的規定次序接受服務。常見的有等 待制、損失制、混合制、閉合制。
- 服務機構:服務台的數量; 服務時間服從的分布
排隊系統的數量指標
- 隊長:系統中的平均顧客數(包括正在接受服務的顧客)。
- 等待隊長:系統中處於等待的顧客的數量。
- 等待時間:等待時間包括顧客的平均逗留時間。
- 忙期:連續保持服務的時長。
數學表示
排隊論中的符號表示
A 輸入過程,B 服務時間,C 服務台數,n 系統容量。
排隊論表示實例 M/M/S/∞
- 輸入過程是 Poisson 流 (顧客到達的時間服從泊松分布,到達的時間間隔便服從負指數分布)
- 服務時間服從負指數分布
- 系統有 S 個服務台平行服務
- 系統容量為無窮大的等待制排隊系統
等待制模型 M/M/S/∞ S=1

單位時間內到達的人數為λ,所以[0,t] 時間內到達的顧客平均數為 λt
**µ代表單位時間服務人的個數 **
判斷模型是否穩定,一般用比較λ和µ的大小(下圖的系統服務強度)

\((1-\rho)\sum_{n=0}^{\infty}n\rho^{n}\),當\(\rho\)<1時候級數收斂
平均等待隊長比平均隊長少一人,因為一人在接受服務。
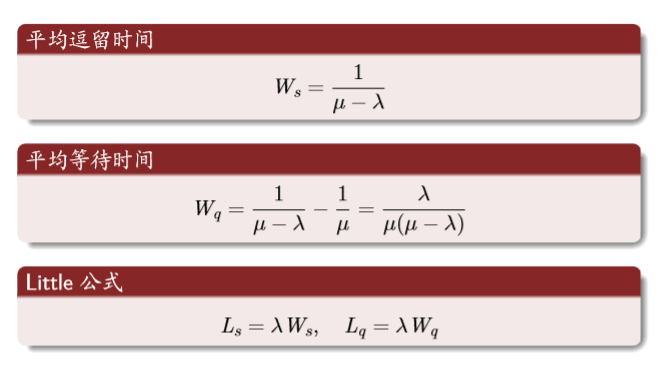
平均等待時間=逗留的時間-服務的時間
Little公式是根據前面推導出來。
實例

λ/µ=8/9<1,系統是穩定的。
平均等待7.1個人
等待制模型 M/M/S/∞ S>1(服務台數量>1)

k=[0:s-1]

實例
案例
- 來訪人員按照 Poisson 流到達,到達速率為 µ = 20 人/小時。
- 接待人員的服務速率間服 λ = 9 人/小時的負指數分布。
- 為使來訪問者等待不超過半小時,最少應配置幾名接待員?
lambda = 20; mu = 9; s = 3;
rho = lambda/(s*mu); %服務強度
k=(0:s-1);
p0 = 1./( sum((s*rho).^k./factorial(k)) + ...
(s*rho)^s/(factorial(s)*(1-rho)) ); %服務台空閑的概率
Ls = s*rho + (s*rho)^s*rho/(factorial(s)*(1-rho)^2)*p0; %平均長度
Ws = Ls/lambda; %平均逗留時間
Wq = Ws - 1/mu%平均等待時間
其他模型
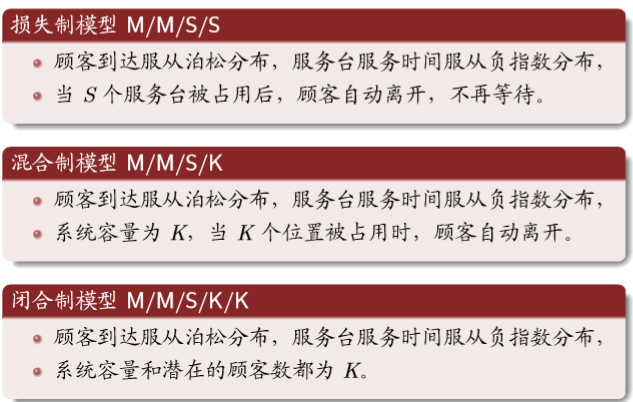
混合制:
系統容量K為隊長,理發店的的凳子數(等待凳子和服務凳子)
閉合制:
工廠的工人,使用的機器。
單服務台
做模擬:
開始服務, 到達, 離開時刻和服務, 等待時長的關系
- 服務時刻(i) = max{到達時刻(i),離開時刻(i−1)}
- 離開時刻(i) = 服務時刻(i) + 服務時長(i)
- 等待時長(i) = 離開時刻(i)−到達時刻(i)
多服務台
開始服務, 到達, 離開時刻和服務, 等待時長的關系
- 服務時刻(i) = max{到達時刻(i),min{服務台空閑時刻}} (假設所有顧客目的盡早的接受服務)
- 所使用服務台(i) = k, 其中 k 使服務台空閑時刻(k) = min
- 離開時刻(i) = 服務時刻(i) + 服務時長(i)
- 服務台空閑時刻(k) = 離開時刻(i)
- 等待時長(i) = 離開時刻(i)−到達時刻(i)(包括服務時間)
自動取款機問題
問題
- 銀行計划安置取款機, A 機價格和平均服務率都是 B 機的 2 倍. 應購置 1 台 A 機還是 2 台 B 機?
- 顧客平均每分鍾到達 1 位,A 型機的平均服務時間為 0.9, B 型機為 1.8 分鍾, 顧客到達間隔和服務時間都服從指數分布.
單服務台
屬於M/M/1/∞ 模型
n = 100000; % 模擬顧客總數
mu = 1; muA = 0.9; % 到達率和服務率
tarr = cumsum(exprnd(mu,1,n));% 到達時刻 ,exprnd生成指數分布(到達的時間間隔)
tsrv = exprnd(muA,1,n); % 服務時長
tsta = zeros(1,n); % 初始化服務時刻
tlea = zeros(1,n);% 初始化離開時刻
twat = zeros(1,n); % 初始化等待時長
tsta(1) = tarr(1);% 首位顧客服務時刻=到達時刻
tlea(1) = tsta(1) + tsrv(1); % 首位顧客離開時刻
twtime(1) = tlea(1) - tarr(1); % 首位顧客等待時長=0
% 上面初始化第一個顧客
for i = 2:n
% 服務時刻 = max{到達時刻, 上一個顧客離開時刻}
tsta(i) = max(tarr(i),tlea(i-1));
tlea(i) = tsta(i) + tsrv(i);% 離開時刻=服務時刻+服務時長
twat(i) = tlea(i) - tarr(i);;% 等待時長=離開時刻-到達時刻
end
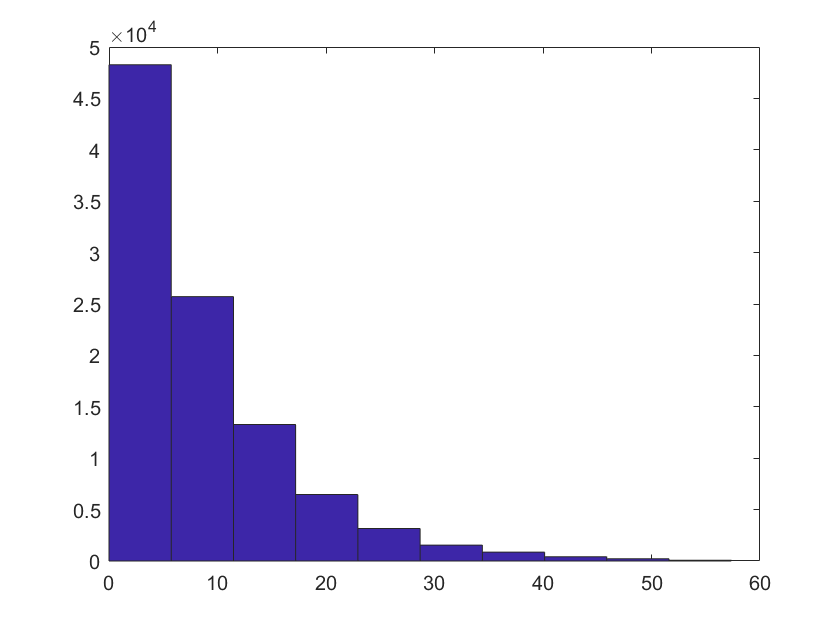
hist(twat)
sum(twat)/n
兩服務台(多個服務台)
n = 100000; % 模擬顧客總數
mu = 1; muB = 1.8; % 到達率和服務率
tarr = cumsum(exprnd(mu,1,n)); % 到達時刻
tsrv = exprnd(muB,1,n);% 服務時長
tsta = zeros(1,n);% 初始化服務/離開時刻
tlea = zeros(1,n); % 初始化等待時長
twat = zeros(1,n);% 初始化服務台結束服務時刻
last = [0 0];%幾個服務台幾個0
for i = 2:n
[minemp, k] = min(last); % 找出最快結束服務的服務台時刻
tsta(i) = max(tarr(i),minemp);% 服務時刻
tlea(i) = tsta(i) + tsrv(i); % 離開時刻
last(k) = tlea(i); % 服務台結束服務時刻
twat(i) = tlea(i) - tarr(i);% 等待時長
end
hist(twat)
sum(twat)/n
真題
2013HIMCM-B: 銀行服務問題

分析
如何生成序列來滿足題意概率分布呢?
舉一個例子,由時間間隔 t = [0 1 2] 和概率 p = [0.2 0.3 0.5] 得到各到顧客達時間間隔 。
-
先把概率p倒過來求前綴和
\[p′ = cumsum([0.5,0.3,0.2]) = [0.5,0.8,1.0] \] -
我們生成隨機數x,則x<=0.5的概率為0.5,0.5<x<=0.8的概率為0.3,0.8<x<=1.0的概率為0.2
\[R = rand(1,5) = [0.1,0.9,0.2,0.4,0.8]; \] -
替換隨機序列的數
把隨機序列R<0.5的數換成2……
由到達時間間隔得到各顧客到達時刻
開始服務, 到達, 離開時刻和服務, 等待時間的關系:
-
開始服務的時刻(i) = max{到達時刻(i),離開時刻 (i-1)}
-
離開時刻(i) = 開始服務的時刻(i) + 服務時間(i)
-
等待時間(i) = 離開時刻(i)−到達時刻(i)−服務時間(i)(不是逗留時刻
代碼
%計算 Tarrival到達時刻, Tservice服務時間
n = 150;
ta = [5 4 3 2 1 0];
pa = [0.05 0.25 0.35 0.10 0.15 0.10];
ts = [ 4 3 2 1 ];
ps = [ 0.15 0.40 0.20 0.25 ];
pacum = cumsum(pa);%遞增
pscum = cumsum(ps);
Tarrival = rand(1,n);
for i = 1:length(pa)
Tarrival(Tarrival<pacum(i)) = ta(i);
end
Tarrival = cumsum(Tarrival);%累加才得到到達時刻
Tservice = rand(1,n);
for i = 1:length(ps)
Tservice(Tservice<pscum(i)) = ts(i);
end
Tstart = zeros(1,n); %開始服務的時刻
Tleave = zeros(1,n); %離開的時刻
Twait = zeros(1,n); %等待的時長
line = zeros(1,n); %隊長
%初始化第一位顧客
Tstart(1) = Tarrival(1);
Tleave(1) = Tstart(1) + Tservice(1);
Twait(1) = Tleave(1) - Tarrival(1) - Tservice(1);
line(1) = 0;
for i = 2:n
Tstart(i) = max(Tleave(i-1), Tarrival(i));
Tleave(i) = Tstart(i) + Tservice(i);
Twait(i) = Tleave(i) - Tarrival(i) - Tservice(i);
%隊長的計算,一直找到前面的人離開了
k = i-1;
while ( k>0 )&&( Tarrival(i)<Tleave(k) )
line(i) = line(i) + 1;
k = k - 1;
end
end
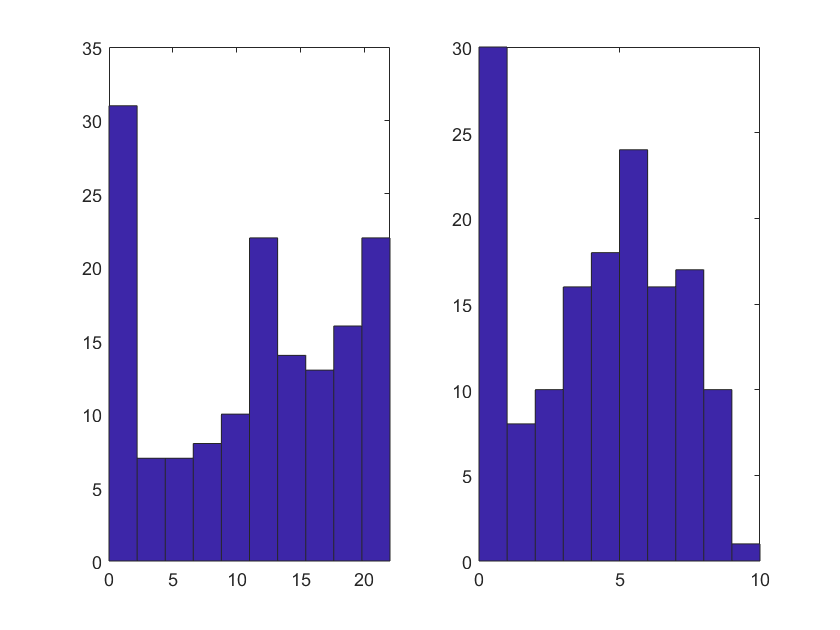
subplot(1,2,1)
hist(Twait)
line
subplot(1,2,2)
hist(line)
因為隨機數,所以可以多算幾次,取平均值。
ICM2017-D: 優化機場安檢口旅客通行
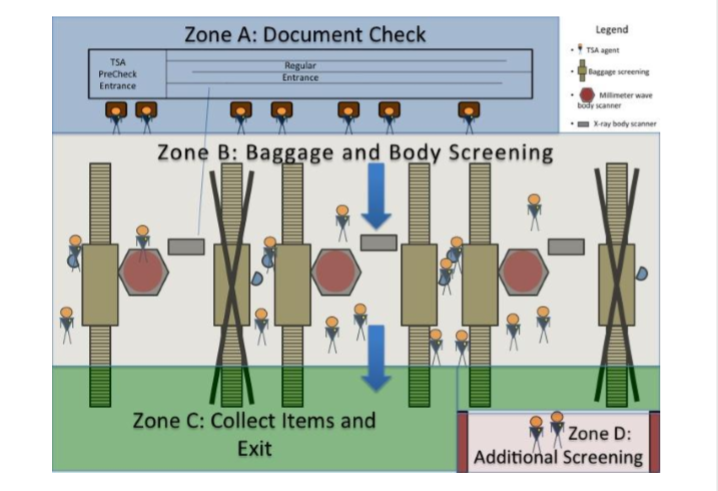
問題
-
建立一個或多個模型,研究旅客通過安檢口的流量,確定瓶 頸,明確判斷當前流程問題區域位置。
-
設計兩個或更多對現有系統德潛在改進,提高旅客通信,減 少等待時間。模擬這些變化展示改進如何影響流程。
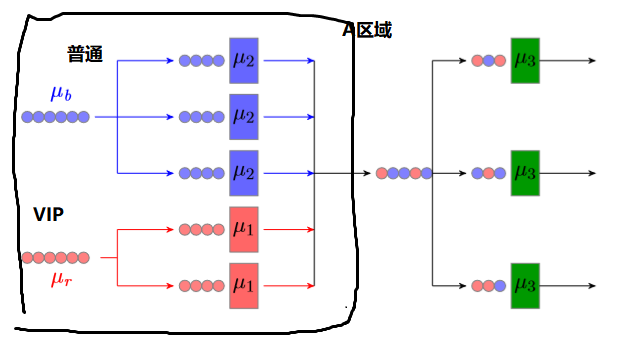
排隊系統: µr = 10, µb = 13, µ1 = 12, µ2 = 9, µ3 = 16
多服務並聯
function [tlea, twat, qlen] = mms(tarr, type, mus)
% MMS Stochastic simulation for M/M/c queue
%
% [tlea, twat, qlen] = mms(tarr, type, mus)
% tarr :每一個顧客到達的時間
% type :客戶類型參數
% mus :服務台的服務速度
% tlea :服務台的離開時間
% twat :服務台的等待時間
% qlen :客戶的隊列長度(排隊的長度)
narr = length(tarr); % 客戶的個數
nsvr = length(mus); % 服務台的數量
% last time at which a customer left a particular server
last = zeros(nsvr,1);
[tsta, tlea, twat, qlen] = deal(zeros(narr,1));
rndm = zeros(nsvr,narr); % rndm(k,i) = 第i個客戶的服務時間
for k = 1:nsvr;
rndm(k,:) = exprnd(mus(k)*type); %生成服從指數分布的隨機數
end
for i = 1:narr
% find booth service was/will be emptied soonest and record
[minemp, ksvr(i)] = min(last);
% start time = max{arrival time, minemp}
tsta(i) = max(tarr(i), minemp);
% severe time = exponential random number with mean parameter mu
tsvr(i) = rndm(ksvr(i),i);
% leaving time = start time + service time
tlea(i) = tsta(i) + tsvr(i);
% last time of k-th server = leaving time of i-th customer
last(ksvr(i)) = tlea(i);
% waiting time = leaving time - arrival time
twat(i) = tlea(i) - tarr(i);
% queue length for i customer
j = i - 1;
while j>0 && tarr(i)<tlea(j)
if ksvr(j)==ksvr(i); qlen(i) = qlen(i) + 1; end
j = j - 1;
end
end
分別求出A區域兩個隊列(紅色和綠色隊列)的離開的時刻,作為下一階段服務台到達的時刻。
具體使用看下面主程序。
串並混合系統
µr = 10, µb = 13, µ1 = 12, µ2 = 9, µ3 = 16
n1 = 2; n2 = 3; n3 = 3;% ni表示第i個服務台的數量
mu1 = 12; mu2 = 9; mu3 = 16;% 服務台的到達率
muR = 10; muB = 13;% 藍色與紅色服務台的服務率
nR = ceil(24*3600/muR); nB = ceil(24*3600/muB);% 服務的人數
tArrR = cumsum(exprnd(muR,nR,1));
tArrB = cumsum(exprnd(muB,nB,1)); %到達時刻
tArr = [tArrR; tArrB];
type = [0.8*ones(nR,1); 1.2*ones(nB,1)];%區分兩種服務的時長
%A區域
[tLeaR, tWatR, qLenR] = mms(tArrR, ones(nR,1), mu1*ones(n1,1));
[tLeaB, tWatB, qLenB] = mms(tArrB, ones(nB,1), mu2*ones(n2,1));
[tArrG, order] = sort([tLeaR; tLeaB]);%輸出為離開A區域的時間,排序進入下一區域
%order數組為排序后的數組在原始數組的位置,保存原來的順序
%下一區域
[tLeaG, tWatG, qLenG] = mms(tArrG, type(order), mu3*ones(n3,1));
tLeaG(order) = tLeaG;
tWatG(order) = tWatG;
qLenG(order) = qLenG;
figure('position',[50,50,1200,600])
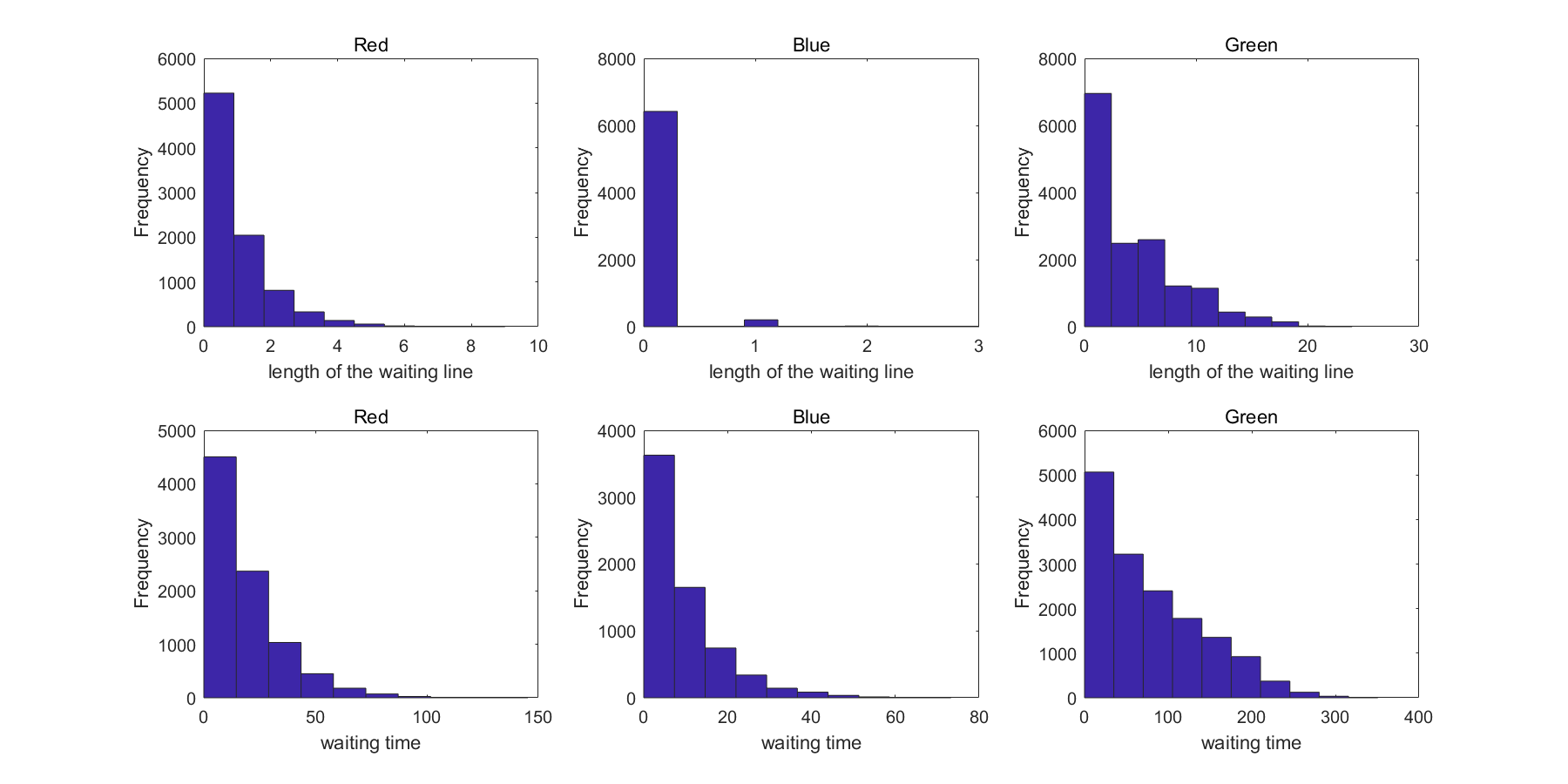
subplot(2,3,1); hist(qLenR); ylabel('Frequency');
xlabel('length of the waiting line'); title('Red')
subplot(2,3,4); hist(tWatR); ylabel('Frequency');
xlabel('waiting time'); title('Red')
subplot(2,3,2); hist(qLenB); ylabel('Frequency');
xlabel('length of the waiting line'); title('Blue')
subplot(2,3,5); hist(tWatB); ylabel('Frequency');
xlabel('waiting time'); title('Blue')
subplot(2,3,3); hist(qLenG); ylabel('Frequency');
xlabel('length of the waiting line'); title('Green')
subplot(2,3,6); hist(tWatG); ylabel('Frequency');
xlabel('waiting time'); title('Green')