2019 ICCV、CVPR、ICLR之視頻預測讀書筆記

2019 ICCV、CVPR、ICLR之視頻預測讀書筆記

作者 | 文永亮

學校 | 哈爾濱工業大學（深圳）

研究方向 | 視頻預測、時空序列預測

ICCV 2019

CVP

github地址：https://github.com/JudyYe/CVP

​ 這是卡耐基梅隆和facebook的一篇paper，這篇論文的關鍵在於分解實體預測再組成，我們觀察到一個場景是由不同實體經歷不同運動組成的，所以這里提出的方法是通過隱式預測獨立實體的未來狀態，同時推理它們之間的相互作用，並使用預測狀態來構成未來的視頻幀，從而實現了對實體分解組成的視頻預測。

​ 該論文使用了兩個數據集，一個是包含可能掉落的堆疊物體ShapeStacks，另一個包含人類在體育館中進行活動的視頻Penn Action，並表明論文的方法可以在這些不同的環境中進行逼真的隨機視頻預測。

​ 主要架構有下面三個部分組成：

1. Entity Predictor（實體預測模塊）: 預測每一個實體表示的未來狀態

2. Frame Decoder（幀解碼器）: 從實體表示中解碼成frame

3. Encoder（編碼器）: 把frame編碼成u作為LSTM的cell-state得到輸出記錄時序信息\(z^1...z^t\)

   （最后其實就是concat進去，見如下:：）

   obj_vecs = torch.cat([pose, bbox, diff_z], dim=-1)
   

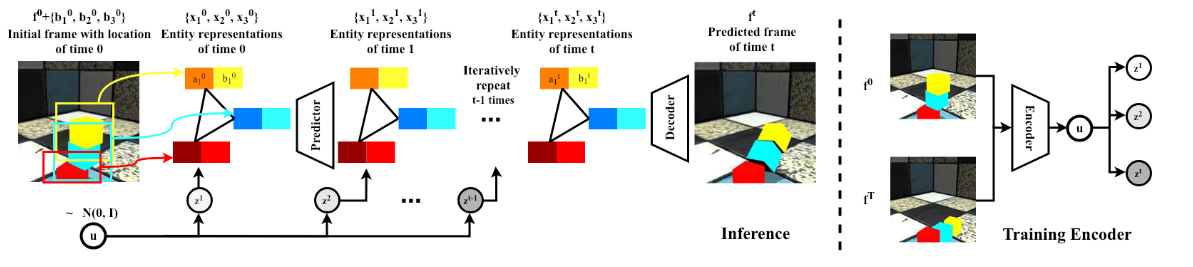
模型將具有已知或者檢測到的實體位置的圖像作為輸入。每個實體均表示為其位置和隱式特征。每個實體的表示為\({x_n^t}^N_{n=1}\equiv\{(b_n^t,a^t_n)\}^N_{n=1}\), \(b_n^t\)表示為預測的位置，\(a^t_n\)表示為隱式特征，這樣的分解方便我們高效地預測每一個實體的未來狀態，給定當前實體表示形式和采樣的潛在變量，我們的預測模塊將在下一個時間步預測這些表示形式。我們所學的解碼器將預測的表示組合為代表預測的未來的圖像。在訓練期間，使用潛在編碼器模塊使用初始幀和最終幀來推斷潛在變量的分布。

分解的思想一般都用mask來體現，就是把變化的與不變的用掩碼表示后在組合起來，預測變化的部分，這是分而治之的思想。

讓\(\left\{\left(\bar{\phi}_{n}, \bar{M}_{n}\right)=g\left(a_{n}\right)\right\}_{n=1}^{N}\)表示在g的網絡結構下解碼每一個實體的特征和空間掩碼，讓\(\mathcal{W}\)表示類似Spatial Transformer Networks的空間變化網絡，可以得到下面的實體的特征和掩碼\(\phi_{n}\)和\(M_n\).

$$ \phi_{n}=\mathcal{W}\left(\bar{\phi}_{n}, b_{n}\right) ; \quad M_{n}=\mathcal{W}\left(\bar{M}_{n}, b_{n}\right) $$ 通過權重掩碼和各個特征的結合最后取平均，這樣我們就得到圖像級別的特征，即每一幀的特征，$M_{bg}$是常數的空間掩碼（論文取值為0.1），其組成的特征表示如下： $$ \phi=\frac{\phi_{b g} \odot M_{b g} {\oplus \sum_{n} \phi_{n} \odot M_{n}}}{M_{b g}\oplus\sum_{n} M_{n}} $$ 上面的公式很好理解，$\odot$是像素乘法，$\oplus$是像素加法，$\phi_{b g} \odot M_{b g} {\oplus \sum_{n} \phi_{n} \odot M_{n}}$這個是加權后的背景特征與加權后的每個實體的特征的總和，最后除以權重和。這樣就得到了解碼的結果。

編碼器的作用是把各幀\(f^0...f^T\)編碼成u，u的分布服從標准正態分布\(\mathcal{N}(0, I)\)，所以需要拉近兩者之間的KL散度，u作為cell-state輸入LSTM得到{\(z_t\)}表示時間序列的隱狀態。

\[L_{e n c}=K L[q(u) \| \mathcal{N}(0, I)] \]

解碼損失就是實體表示\(\hat{x}_{n}^{t}\)經過解碼與真實圖像\(\hat{f}^{t}\)的L1損失。

\[L_{d e c}=\sum_{t=0}^{T}\left\|\mathcal{D}\left(\left\{\hat{x}_{n}^{t}\right\}, f^{0}\right)-\hat{f}^{t}\right\|_{1} \]

預測損失即為解碼損失加上位置損失$$\sum_{n=1}^{{N}\left|b_{n}}{t}-\hat{b}_{n}^{t}\right|{2}$$.

\[L_{p r e d}=\sum_{t=1}^{T}\left(\left\|\mathcal{D}\left(\left\{x_{n}^{t}\right\}, f^{0}\right)-\hat{f}^{t}\right\|_{1}+\lambda_{1} \sum_{n=1}^{N}\left\|b_{n}^{t}-\hat{b}_{n}^{t}\right\|^{2}\right) \]

其總的損失函數即三個損失的和。

\[L=L_{d e c}+L_{p r e d}+\lambda_{2} L_{e n c} \]

Non-Local ConvLSTM

github地址：https://github.com/xyiyy/NL-ConvLSTM (Code will be published later)

Non-Local ConvLSTM是復旦大學和b站的論文，其實這篇不太算視頻預測方向，這是使用了在ConvLSTM中使用Non-Local結合前一幀增強圖像減少視頻壓縮的偽影，是視頻壓縮的領域，但是對我有些啟發，Non-Local最初就是用於視頻分類的。

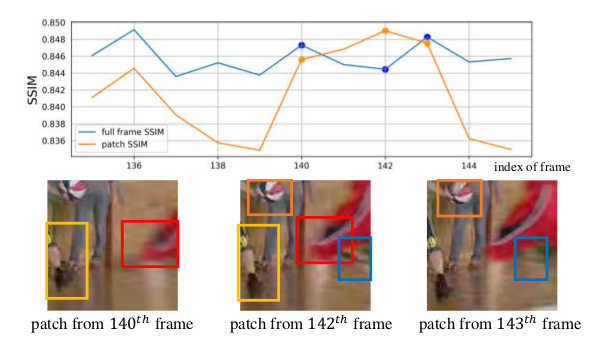
SSIM是用來評價整張圖的質量，但是對於一張質量不好的圖來說他的patch並不一定差，對於一張好圖來說他的patch也不一定好，所以作者用Non-Local來捕捉兩幀之間特征圖間像素的相似性。

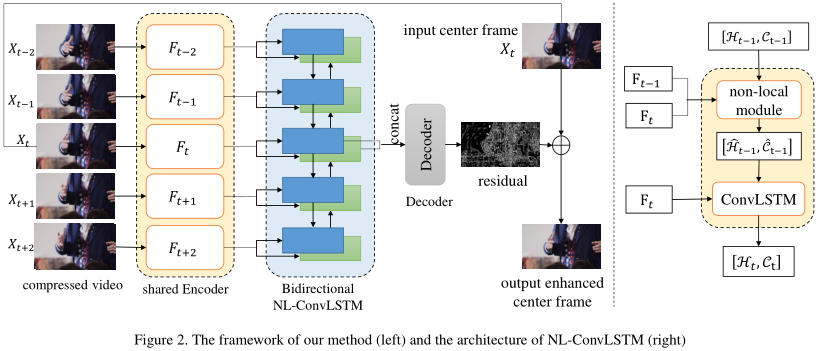
ConvLSTM可以表示成下面的公式：

\[\left[\mathcal{H}_{t}, \mathcal{C}_{t}\right]=\operatorname{Conv} L S T M\left(F_{t},\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right]\right) \]

即hidden state (\(H_t,C_t\)) 是從上一次的hidden state (\(H_{t_1},C_{t-1}\)) 和\(F_t\) 經過ConvLSTM-cell得到的。

而NL-ConvLSTM是在ConvLSTM的基礎上加了Non-local的方法，可以表示如下：

\[\begin{aligned} S_{t} &=N L\left(F_{t-1}, F_{t}\right) \\\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] &=N L W \operatorname{arp}\left(\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right], S_{t}\right) \\\left[H_{t}, C_{t}\right] &=\operatorname{Conv} L S T M\left(F_{t},\left[\hat{\mathcal{H}}_{t-1}, \hat{c}_{t-1}\right]\right) \end{aligned} \]

​ 其中\(S_{t} \in \mathbb{R}^{N \times N}\)是當前幀\(F_t\) 與前一幀的\(F_{t-1}\) 的相似矩陣，這里的Non-Local的操作是一種特殊的attention，這不是self-attention，是比較前一幀獲得相似矩陣再計算attention，NLWrap操作可以用數學表達如下：

\[\begin{aligned} D_{t}(i, j) &=\left\|F_{t-1}(i)-F_{t}(j)\right\|_{2} \\ S_{t}(i, j) &=\frac{\exp \left(-D_{t}(i, j) / \beta\right)}{\sum_{\forall i} \exp \left(-D_{t}(i, j) / \beta\right)} \\\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] &=\left[\mathcal{H}_{t} \cdot S_{t}, \mathcal{C}_{t} \cdot S_{t}\right] \end{aligned} \]

這里的公式估計論文寫錯了，我認為是：

\[\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] =\left[\mathcal{H}_{t-1} \cdot S_{t}, \mathcal{C}_{t-1} \cdot S_{t}\right] \]

但是由於Non-local計算量太大，作者提出了兩階段的Non-Local相似度估計，即池化之后做相似度計算如下：

ICLR 2019

SAVP

github地址：https://github.com/alexlee-gk/video_prediction

​ 當我們與環境中的對象進行交互時，我們可以輕松地想象我們的行為所產生的后果：推一顆球，它會滾走；扔一個花瓶，它會碎掉。視頻預測中的主要挑戰是問題的模棱兩可，未來的發展方向似乎有太多。就像函數的導數能夠預測該值附近的走向，當我們預測非常接近的未來時我們能夠未來可期，可是當可能性的空間超出了幾幀之后，並且該問題本質上變成了多模的，即預測就變得更多樣了。

​ 這篇把GAN和VAE都用在了視頻預測里，其實GAN-VAE在生成方面早有人結合，只是在視頻預測中沒有人提出，其實提出的SAVP是SV2P (Stochastic Variational Video Prediction) 和SVG-LP (Stochastic Video Generation with a Learned Prior) 的結合。

SV2P網絡結構

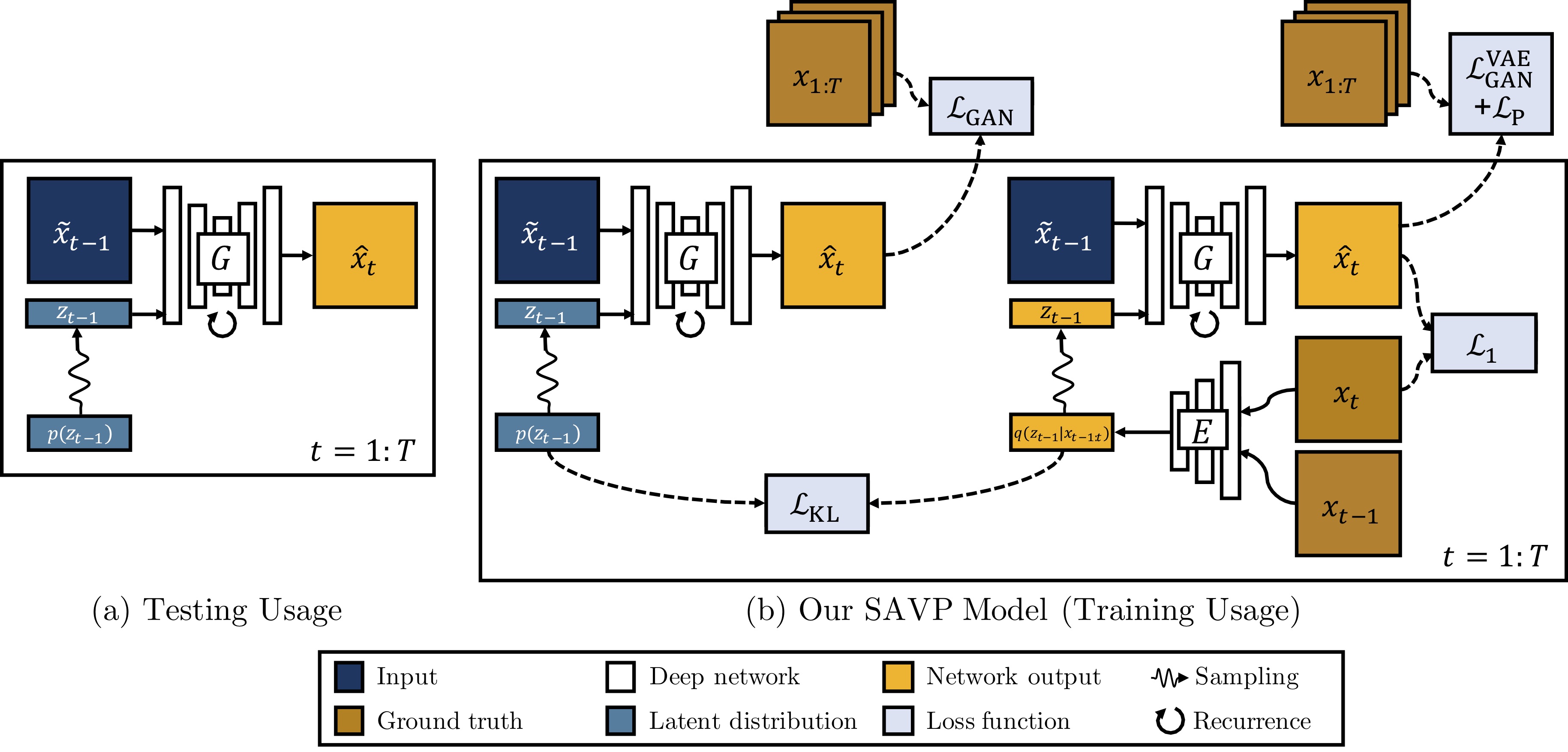
​ 在訓練期間，隱變量從\(q(z_{t-1}|x_{t-1:t})\)中采樣，對每一幀的生成都可以看作是對\(\hat{x}_{t}\)的重構，\(x_t\)與\({x}_{t-1}\)被Encoder編碼為隱變量\(z_{t-1}\)，前一幀\(x_{t-1}\)與隱變量\(z_{t-1}\)經過G模型之后得到預測幀\(\hat{x}_t\)要計算與當前幀\(x_t\)的\(L_1\)損失，使其生成要盡量相似。

\[\mathcal{L}_{1}(G, E)=\mathbb{E}_{\mathbf{x}_{0: T}\left.\mathbf{z}_{t} \sim E\left(\mathbf{x}_{t: t+1}\right)\right|_{t=0} ^{T-1}}{\left[\sum_{t=1}^{T}\left\|\mathbf{x}_{t}-G\left(\mathbf{x}_{t-1}, \mathbf{z}_{t-1}\right)\right\|_{1}\right]}. \]

​ 在測試階段我們的隱變量從先驗分布\(p(z_{t-1})\)直接采樣，\(z_{t-1}\)與\(\tilde{x}_{t-1}\) 經過G生成下一幀的預測圖\(\hat{x}_t\) ，所以需要同時拉近\(q(z_{t-1}|x_{t-1:t})\)與\(p(z_{t-1})\)的分布，其KL散度如下：

\[\mathcal{L}_{\mathrm{KL}}(E)=\mathbb{E}_{\mathbf{x}_{0: T}}\left[\sum_{t=1}^{T} \mathcal{D}_{\mathrm{KL}}\left(E\left(\mathbf{x}_{t-1: t}\right) \| p\left(\mathbf{z}_{t-1}\right)\right)\right] \]

​ 所以G和E的目標函數如下：

\[G^{*}, E^{*}=\arg \min _{G, E} \lambda_{1} \mathcal{L}_{1}(G, E)+\lambda_{\mathrm{KL}} \mathcal{L}_{\mathrm{KL}}(E) \]

​ \(L_1\)損失並不是很能反映圖像的相似度，既然文章是VAE和GAN的結合，所以在下面提出了判別器去評判圖片質量。論文指出單純的VAE更容易產生模糊圖，這里加入的判別器是能夠分辨出生成視頻序列\(\hat{x}_{1:T}\)與真實視頻序列\(x_{1:T}\)，這里是比較意想不到的地方，因為這里沒有使用直接的圖像判別器，而是判別生成序列與真實序列，其D判別器的網絡結構是使用了3D卷積基於SNGAN的，G生成器是使用了convLSTM捕捉時空序列信息。

\[\mathcal{L}_{\mathrm{GAN}}(G, D)=\mathbb{E}_{\mathbf{x}_{1: T}}\left[\log D\left(\mathbf{x}_{1: T}\right)\right]+\mathbb{E}_{\left.\mathbf{x}_{1: T}, \mathbf{z}_{t} \sim p\left(\mathbf{z}_{t}\right)\right)_{t=0}^{T-1}}\left[\log \left(1-D\left(G\left(\mathbf{x}_{0}, \mathbf{z}_{0: T-1}\right)\right)\right)\right] \]

​ 最后總的損失函數如下：

\[G^{*}, E^{*}=\arg \min _{G, E} \max _{D, D^{\mathrm{ME}}} \lambda_{1} \mathcal{L}_{1}(G, E)+\lambda_{\mathrm{KL}} \mathcal{L}_{\mathrm{KL}}(E)+\mathcal{L}_{\mathrm{GAN}}(G, D)+\mathcal{L}_{\mathrm{GAN}}^{\mathrm{VAE}}\left(G, E, D^{\mathrm{VAE}}\right) \]

​ 下面是論文中的實驗結果：

CVPR 2019

MIM

github地址：https://github.com/Yunbo426/MIM

這是清華大學的一篇paper，作者Yunbo Wang也是Eidetic 3D LSTM，PredRNN++，PredRNN的作者，自然時空序列的發生過程常常是非平穩（ Non-Stationarity ）的，在低級的非平穩體現在像素之間的空間相關性或時序性，在高層語義特征的變化其實體現在降水預報中雷達回波的積累，形變或耗散。

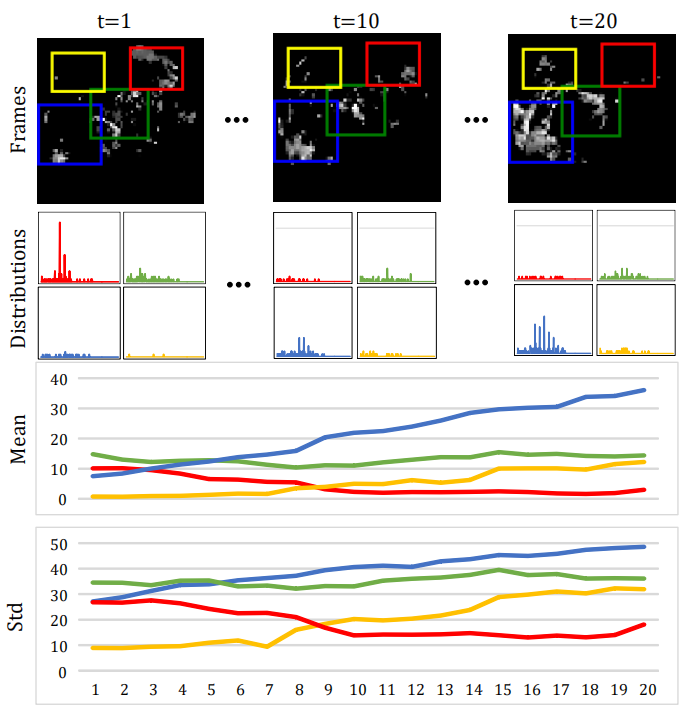
上圖是連續20幀雷達圖變化，其中白色像素表示降水概率較高。第二、第三、最后一行：通過不同顏色的邊框表明相應局部區域的像素值分布、均值和標准差的變化。藍色和黃色框表明着生成的非平穩變化過程，紅色框表明了消散的過程，綠色框為形變過程。

左邊為ST-LSTM（Spatio-Temporal LSTM），右邊為加入了MIM模塊的LSTM

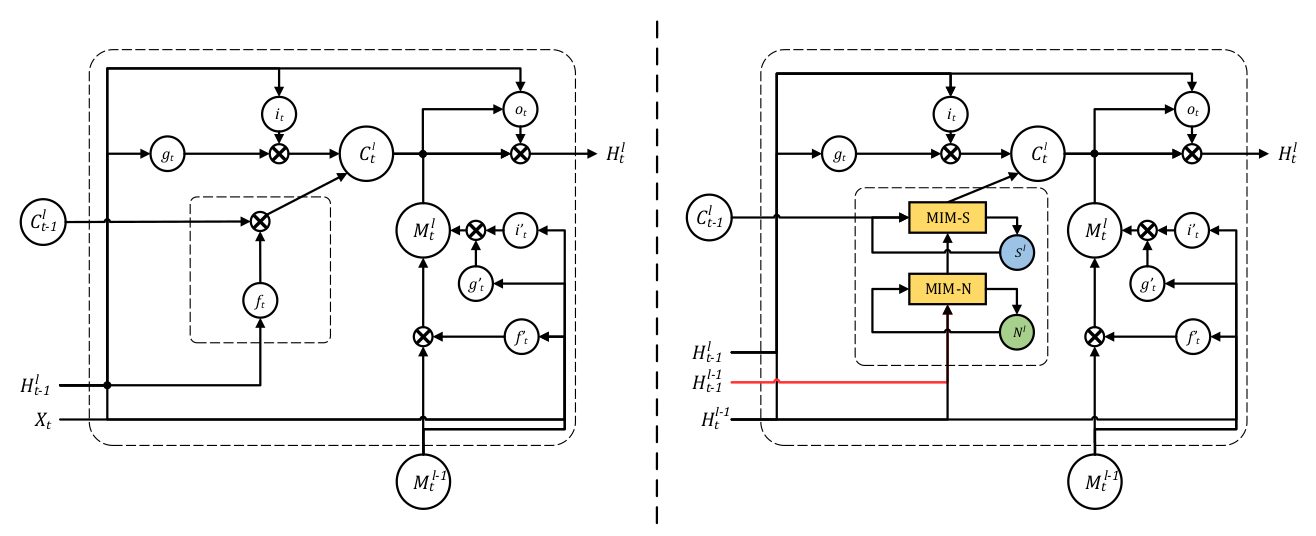
這篇論文的主要工作就是構造了MIM模塊代替遺忘門，其中這個模塊分為兩部分：MIM-N（非平穩模塊），MIM-S（平穩模塊）。

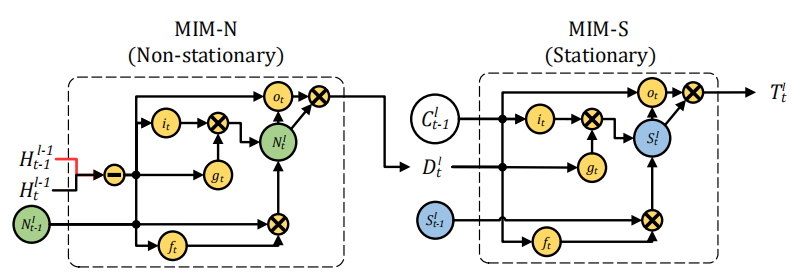
MIM-N所有的門\(g_t\)，\(i_t\)， \(f_t\) ，和\(o_t\)都用\(\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)\) 短期記憶的隱狀態的幀差更新，因為這樣強調了非平穩變換，最后得到特征差\(D_t^l\)和\(C^l_{t-1}\)作為MIM-S輸入，MIM-S會根據原記憶\(C^l_{t-1}\)和特征差\(D_t^l\)決定變化多少，如果\(D_t^l\) 很小，意味着並不是非平穩變化，即變化得平穩，MIM-S很大程度會繼續沿用\(C^l_{t-1}\)；如果\(D_t^l\) 很大，則會重寫記憶並且更關注於非平穩變化。

其數學表達式如下：

1. MIM-N：

\[ \begin{array}{l}{g_{t}=\tanh \left(W_{x g} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n g} * \mathcal{N}_{t-1}^{l}+b_{g}\right.} \\ {i_{t}=\sigma\left(W_{x i} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n i} * \mathcal{N}_{t-1}^{l}+b_{i}\right)} \\ {f_{t}=\sigma\left(W_{x f} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n f} * \mathcal{N}_{t-1}^{l}+b_{f}\right)} \\ {\mathcal{N}_{t}^{l}=f_{t} \odot \mathcal{N}_{t-1}^{l}+i_{t} \odot g_{t}} \\ {o_{t}=\sigma\left(W_{x o} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n o} * \mathcal{N}_{t}^{l}+b_{o}\right)} \\ {\mathcal{D}_{t}^{l}=\operatorname{MIM-N}\left(\mathcal{H}_{t}^{l-1}, \mathcal{H}_{t-1}^{l-1}, \mathcal{N}_{t-1}^{l}\right)=o_{t} \odot \tanh \left(\mathcal{N}_{t}^{l}\right)}\end{array} \]

2. MIM-S:

   \[ \begin{array}{l}{g_{t}=\tanh \left(W_{d g} * \mathcal{D}_{t}^{l}+W_{c g} * \mathcal{C}_{t-1}^{l}+b_{g}\right)} \\ {i_{t}=\sigma\left(W_{d i} * \mathcal{D}_{t}^{l}+W_{c i} * \mathcal{C}_{t-1}^{l}+b_{i}\right)} \\ {f_{t}=\sigma\left(W_{d f} * \mathcal{D}_{t}^{l}+W_{c f} * \mathcal{C}_{t-1}^{l}+b_{f}\right)} \\ {S_{t}^{l}=f_{t} \odot \mathcal{S}_{t-1}^{l}+i_{t} \odot g_{t}} \\ {o_{t}=\sigma\left(W_{d o} * \mathcal{D}_{t}^{l}+W_{c o} * \mathcal{C}_{t-1}^{l}+W_{s o} * S_{t}^{l}+b_{o}\right)} \\ {\mathcal{T}_{t}^{l}=\operatorname{MIM-S}\left(\mathcal{D}_{t}^{l}, \mathcal{C}_{t-1}^{l}, \mathcal{S}_{t-1}^{l}\right)=o_{t} \odot \tanh \left(\mathcal{S}_{t}^{l}\right)}\end{array} \]

   這一篇的實驗做的很全面，其效果如下，均達到了state-of-the-art：

Moving Mnist：

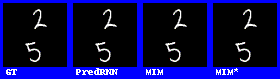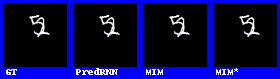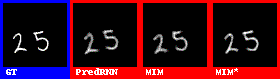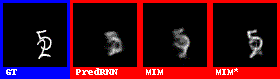
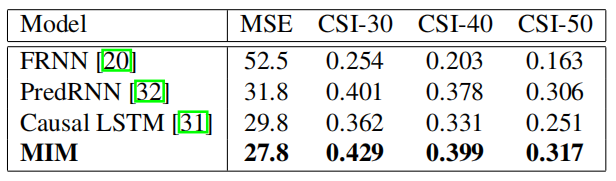
在數字集上的表現效果較好。

Radar Echo：

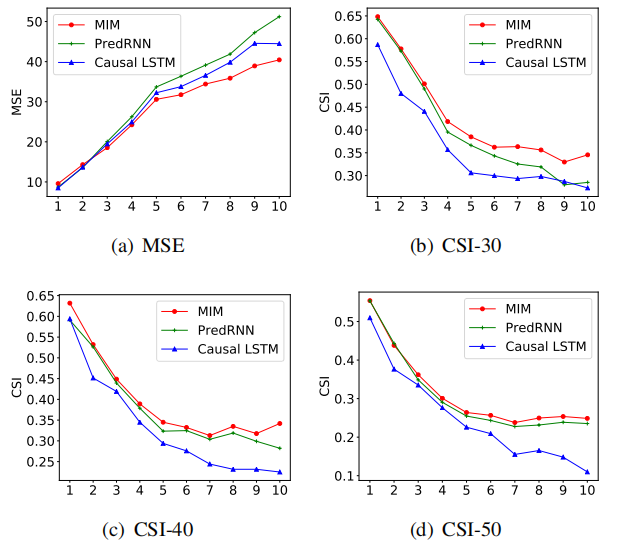
其實可以看到MSE在預測第五幀才有明顯的優勢，CSI-40和CSI-50其實並沒有明顯優勢。

總結

視頻預測是結合了時空序列信息的預測，其關鍵在於如何利用時序信息，ConvLSTM就是把卷積直接與LSTM結合記錄時序信息，而在VAE相關的模型中時間序列被編碼成隱變量拼接起來。除了修改LSTM-cell的結構(e.g. MIM)或者其他的網絡結構嘗試捕捉其他信息，我們常見的一種思想就是分而治之，把變與不變用掩碼區分出來，有點像我之前解讀的一篇BANet，這里的CVP方法甚至對實體直接進行預測，這些都是比較好的想法。