原地址:
GMM與K-means聚類效果實戰
備注
分析軟件:python
數據已經分享在百度雲:客戶年消費數據
密碼:lehv
該份數據中包含客戶id和客戶6種商品的年消費額,共有440個樣本
正文
一、數據探索和預處理
1.讀取數據
import numpy as np import pandas as pddata = pd.read_excel(r'C:\Users\user\Desktop\客戶年消費數據.xlsx')
2.缺失檢查
print('各字段缺失情況:\n', data.isnull().sum())
輸出:
id 0
Fresh 0
Milk 0
Grocery 0
Frozen 0
Detergents_Paper 0
Delicatessen 0
dtype: int64
觀察得出:數據不存在缺失,且數據類型都為整數數值型
3.不同商品消費額分布
為了避免分布圖右偏嚴重,剔除了大於95%分位數的極端值
import matplotlib.pyplot as plt import seaborn as sns六種商品年消費額分布圖
fig = plt.figure(figsize=(16, 9))
for i, col in enumerate(list(data.columns)[1:]):
plt.subplot(321+i)
q95 = np.percentile(data[col], 95)
sns.distplot(data[data[col] < q95][col])
plt.show()
輸出: 
從圖中看出:商品年消費額基本符合大於0的正態分布
4.極值和異常值處理
features = data[['Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper', 'Delicatessen']]
# 剔除極值或異常值
ids = []
for i in list(features.columns):
q1 = np.percentile(features[i], 25)
q3 = np.percentile(features[i], 75)
intervel = 1.6*(q3 - q1)/2
low = q1 - intervel
high = q3 + intervel
ids.extend(list(features[(features[i] <= low) |
(features[i] >= high)].index))
ids = list(set(ids))
features = features.drop(ids)
二、無監督學習-降維和聚類分析
1.整體思路
數據中沒有沒有明顯的目標變量,因此只能對客戶的消費特征進行分析,也就是機器學習中所指的無監督方法。這里利用K-means和GMM(Gaussian Mixture Model)兩種聚類算法,嘗試對客戶進行聚類分析,並對比兩種算法的聚類結果差異。為了方便分析聚類效果,先用PCA算法降六個特征維度降低到兩維。
2.聚類算法原理簡述
K-means聚類
該算法利用數據點之間的歐式距離大小,將數據划分到不同的類別,歐式距離較短的點處於同一類。算法結果直接返回的是數據點所屬的類別。
GMM
全稱Gaussian Mixture Model,可以簡單翻譯為高斯混合模型,Gaussian指高斯分布(也就是正態分布)。該算法假設所有數據點來自多個參數不同的高斯分布,來自同一分布的數據點被划分為同一類。算法結果返回的是數據點屬於不同類別的概率。
3.數據降至二維(PCA)
# 計算每一列的平均值 meandata = np.mean(features, axis=0) # 均值歸一化 features = features - meandata # 求協方差矩陣 cov = np.cov(features.transpose()) # 求解特征值和特征向量 eigVals, eigVectors = np.linalg.eig(cov) # 選擇前兩個特征向量 pca_mat = eigVectors[:, :2] pca_data = np.dot(features , pca_mat) pca_data = pd.DataFrame(pca_data, columns=['pca1', 'pca2'])兩個主成分的散點圖
plt.subplot(111)
plt.scatter(pca_data['pca1'], pca_data['pca2'])
plt.xlabel('pca_1')
plt.ylabel('pca_2')
plt.show()
輸出: 
說明:圖2.1中,橫軸代表第一主成分,縱軸代表第二主成分
4.數據降維后信息保留百分比
print('前兩個主成分包含的信息百分比:{:.2%}'.format(np.sum(eigVals[:2])/np.sum(eigVals)))
輸出:
前兩個主成分包含的信息百分比:92.39%
5.客戶聚類
該步驟中,主要是對降維后的二維數據進行GMM和K-means聚類。聚類類別分別為2,3,4,5時,對比時兩種算法下,點的的划分結果,並以散點圖展現。
先定義make_ellipses函數,用於畫出GMM算法中的高斯分布區域:
import matplotlib as mpl定義make_ellipses函數,根據GMM算法輸出的聚類類別,畫出相應的高斯分布區域
def make_ellipses(gmm, ax, k):
for n in np.arange(k):
if gmm.covariance_type == 'full':
covariances = gmm.covariances_[n][:2, :2]
elif gmm.covariance_type == 'tied':
covariances = gmm.covariances_[:2, :2]
elif gmm.covariance_type == 'diag':
covariances = np.diag(gmm.covariances_[n][:2])
elif gmm.covariance_type == 'spherical':
covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
v, w = np.linalg.eigh(covariances)
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan2(u[1], u[0])
angle = 180 * angle / np.pi # convert to degrees
v = 2. * np.sqrt(2.) * np.sqrt(v)
ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
180 + angle)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.3)
ax.add_artist(ell)
再根據模型輸出,畫出聚類結果對比圖:
from sklearn.cluster import KMeans from sklearn.mixture import GaussianMixture from sklearn.metrics import silhouette_scorescore_kmean = []
score_gmm = []
random_state = 87
n_cluster = np.arange(2, 5)
for i, k in zip([0, 2, 4, 6], n_cluster):
# K-means聚類
kmeans = KMeans(n_clusters=k, random_state=random_state)
cluster1 = kmeans.fit_predict(pca_data)
score_kmean.append(silhouette_score(pca_data, cluster1))# gmm聚類 gmm = GaussianMixture(n_components=k, covariance_type='full', random_state=random_state) cluster2 = gmm.fit(pca_data).predict(pca_data) score_gmm.append(silhouette_score(pca_data, cluster2)) # 聚類效果圖 plt.subplot(421+i) plt.scatter(pca_data['pca1'], pca_data['pca2'], c=cluster1, cmap=plt.cm.Paired) if i == 6: plt.xlabel('K-means') plt.subplot(421+i+1) plt.scatter(pca_data['pca1'], pca_data['pca2'], c=cluster2, cmap=plt.cm.Paired) make_ellipses(gmm, ax, k) if i == 6: plt.xlabel('GMM')
plt.show()
輸出: 
說明:聚類類別分別為2,3,4,5時,兩種聚類算法結果對比(左邊是K-means,右邊是GMM);點的顏色相同代表被聚為同一類;右圖中的透明橢圓區域,代表GMM算法估計出的隱藏高斯分布區域。
三、聚類效果分析
如何評判聚類結果呢?這里引入輪廓分析(Silhouette analysis),輪廓分析主要統計輪廓得分,該指標計算聚類類別與相鄰類別之間的總體距離大小,從而判斷聚類有效程度。
# 聚類類別從2到11,統計兩種聚類模型的silhouette_score,分別保存在列表score_kmean 和score_gmm score_kmean = [] score_gmm = [] random_state = 87 n_cluster = np.arange(2, 12) for k in n_cluster: # K-means聚類 kmeans = KMeans(n_clusters=k, random_state=random_state) cluster1 = kmeans.fit_predict(pca_data) score_kmean.append(silhouette_score(pca_data, cluster1)) # gmm聚類 gmm = GaussianMixture(n_components=k, covariance_type='spherical', random_state=random_state) cluster2 = gmm.fit(pca_data).predict(pca_data) score_gmm.append(silhouette_score(pca_data, cluster2))得分變化對比圖
sil_score = pd.DataFrame({'k': np.arange(2, 12),
'score_kmean': score_kmean,
'score_gmm': score_gmm})K-means和GMM得分對比
plt.figure(figsize=(10, 6))
plt.bar(sil_score['k']-0.15, sil_score['score_kmean'], width=0.3,
facecolor='blue', label='Kmeans_score')
plt.bar(sil_score['k']+0.15, sil_score['score_gmm'], width=0.3,
facecolor='green', label='GMM_score')
plt.xticks(np.arange(2, 12))
plt.legend(fontsize=16)
plt.ylabel('silhouette_score', fontsize=16)
plt.xlabel('k')
plt.show()
輸出: 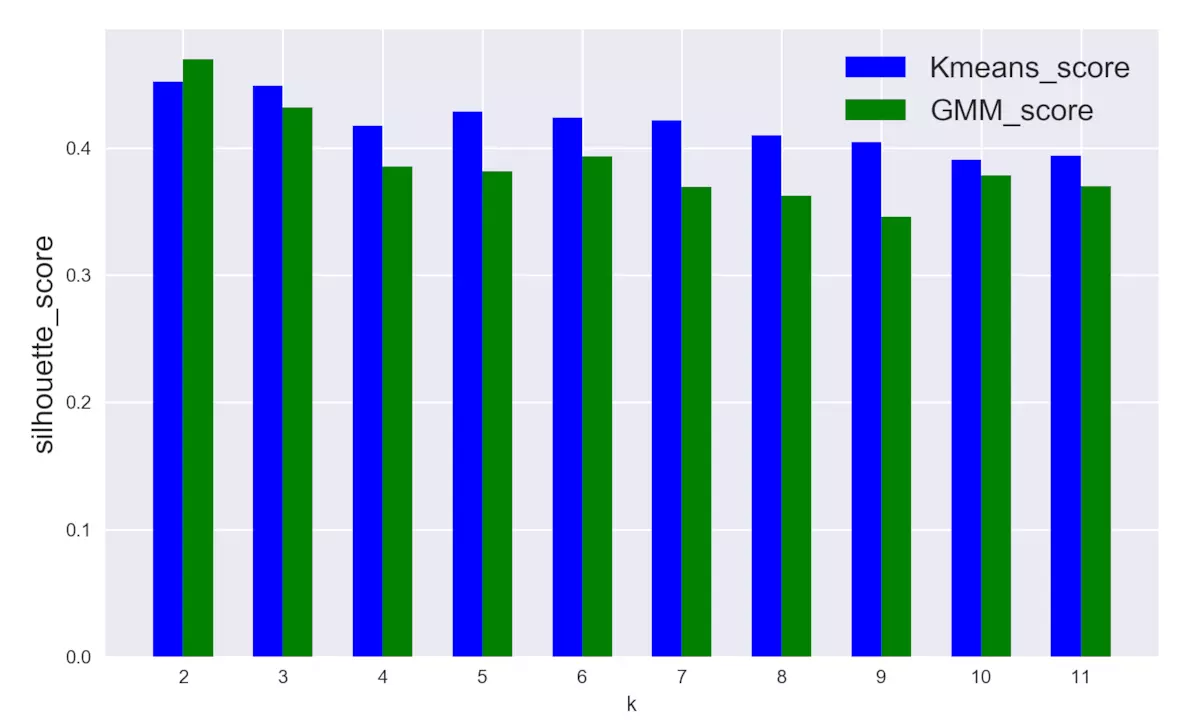
四、小結和建議
經過本次探索過程,總結以下幾點:
1.圖2.2,從點的划分情況來看,GMM和K-means的聚類結果具有較強的相似性;
2.圖3.1, 從對比的角度,以silhouette_score為評判指標,整體上GMM的模型得分略低於K-means;
3.圖3.1,聚類類別增多時,K-means模型的得分比較穩定,幾乎沒有明顯差別,相比之下,GMM模型的得分開始下降幅度較大,但之后也趨於穩定。
4.根據得分情況,最佳聚類類別應該為2或3,此時K-means和GMM模型的表現都比較好。
5.最優k值對應的聚類類別可以作為新的數據特征,用於其它分析。
個人建議:若不考慮運算速度,當兩種算法聚類得分差異很小時,推薦使用GMM算法,因為GMM能輸出數據點屬於某一類別的概率,因此輸出的信息豐富程度大大高於K-means算法。
以上為轉載內容。
在照葫蘆畫瓢的時候,遇到一點問題,主要是網絡導致的python庫文件下載速度慢和一點程序上的小問題。把兩個下載時速度慢的庫sklearn和xlrd放在github上了,整個python文件也在。
Github-GMM
sklearn.mixture.GaussianMixture 官方操作手冊
從手冊上查到
gmm.means_ //可以查看均值
gmm.covariances_ //可以查看均方差
