凸優化學習筆記

在優化問題中，尋找最優解過程中兩個基本的難點：一是局部最優不一定是全局最優，而通過各類算法找到的最優值往往是局部最優值；其次便是約束條件的復雜性導致求解算法的復雜性大幅度增加。凸優化問題的優勢在於其局部最優解就是全局最優解，技巧與難點體現在描述問題的環節，一旦問題被建模為凸優化問題，求解過程相對來說就非常簡單。

1 基本概念

1.1 仿射集

若集合 \(C\subseteq R^{n}\) 中任意兩個不同點的直線仍在集合 \(C\) 中，那么集合\(C\)是仿射的。根據上述定義，可以將 \(C\subseteq R^{n}\) 是仿射的等價為：對於任意的 \(x_1,x_2 \in C\) 及 \(θ∈R\) 有 \(θx_1+(1-θ)x_2∈C\)。這個概念可以拓展到多個點的情況有：對任意 \(x_1,...,x_k∈C\) 並且 \(θ_1+⋯+θ_k=1\) 其中 \(θ_1,…,θ_k∈R\) ，那么 \(θ_1 x_1+,…,+θ_k x_k\) 仍然在 \(C\) 中。

1.2 凸集

仿射集中定義的是任意點確定的直線上的點均在仿射集內，凸集中則定義為任意點確定的線段上的點均在凸集內，按照線段的定義，可以將θ的條件更改為$$θ_i≥0，θ_i∈R，i=1,…,k$$ $$θ_1+⋯+θ_k=1$$以符合凸集的定義。

1.3 凸函數

1.3.1 凸函數定義與性質

有函數 \(f:R^n→R\) ，如果對於任意的 \(x,y∈dom\ f\) 且 $dom\ f $ 也為凸集，並且 \(0≤θ≤1\) ，有$$f(θx+(1-θ)y)≤θf(x)+(1-θ)f(y)$$那么函數 $f:R^n→R $ 是凸函數。從幾何意義上看，上述式子意味着在點 \((x,f(x))\) 和點 \((y,f(y))\) 之間的線段，在函數 \(f\) 的圖像上方。

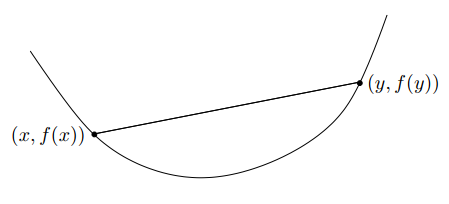 圖1-1 凸函數示意圖 凸函數的另一個性質：有函數 $f:R^n→R$ ，如果對於任意的 $x∈dom\ f$ 且 $dom\ f$ 也為凸集，$v∈R^n$，若函數 $g(t)=f(x+tv)$為凸函數，其中$dom\ g = \{t|x+tv∈dom\ f\}$，則函數$f$為凸函數。這一性質可以理解為：若函數是凸的，則當且僅當其在與其定義域相交的任何直線上都是凸的。 上述的兩點凸函數性質中，第一個性質較為實用，第二個性質更適合於理論分析。 ###1.3.2 凸函數一階條件與二階條件 凸函數的一階及二階條件也經常被用來判定函數是否為凸函數。對於一階條件來說，若函數 $f:R^n→R$ 是凸函數，則有式$$f(y)≥f(x)+∇f(x)^T (y-x)$$成立。其中函數$f$可微，$x,y∈dom\ f$ 且 $dom\ f$ 也為凸集。上述條件為充要條件。 對於二階條件，設函數 $f:R^n→R$二階可微，則$$f為凸函數⇔∀x∈dom f,∇^2 f(x)≽0$$其中$x∈dom \ f$ 且 $dom\ f$ 也為凸集。 ##1.4 擬凸函數 對於函數$f:R^n→R$，若其定義域及所有下水平集（α-sublevel set） $$S_α = \{x∈dom\ f | f(x)≤α\}$$α∈R，都是凸集，則函數f為擬凸函數。由定義可以得出，下水平集其實是函數f定義域的某個區間，同時也可以得出凸函數是擬凸函數的一種特殊情況。 #2 保凸運算 在凸優化的實際運用或理論推導計算過程中，有時可以將簡單的凸函數構造成新的、復雜的凸函數，使其更加適合解決問題。這種構造新的凸函數過程就叫做保凸運算，其核心就是構造后的函數還能保證其凸性。 ##2.1 非負加權和 若函數 $f_i (i=1,…,m)$為凸函數，則$$f= w_1 f_1+⋯+w_m f_m$$依然是凸函數。 ##2.2 復合仿射映射 有函數 $f:R^n→R$，並且$A∈R^{m×n}$，$b∈R^n$，定義函數$g:R^m→R$為 $$g(x)=f(Ax+b)$$其中$ dom\ g=\{x\ |\ Ax+b∈dom f \}$。則有：若$f$為凸函數，則$g$也為凸函數。

2.3 復合函數

給定函數\(h:R^k→R\)和\(g:R^n→R^k\)，定義復合函數\(f=h°g:R^n→R\)為

\[f(x)=h(g(x)),dom\ f=\{x∈dom g\ |\ g(x)∈dom\ h\}$$則函數f的保凸與保凹滿足的結論如下，其中函數$g$和$h$二次可微並且定義域均為$R$。 若$h$為凸且非減，$g$為凸，則f為凸函數。 若$h$為凸且非增，$g$為凹，則f為凸函數。 若$h$為凹且非減，$g$為凹，則f為凹函數。 若$h$為凸且非增，$g$為凸，則f為凹函數。 #3 凸優化問題 優化問題的一般形式如下式所示。 $$minimize\ f_0 (x)$$$$subject\ to\ f_i (x)≤0，i=1,…,m$$$$h_i (x)=0，i=1,…,p$$稱x∈R^n為優化變量，$f_0:R^n→R$為目標函數，$f_i (x)≤0$為不等式約束，對應的$f_i (x)$為不等式約束函數，$h_i (x)≤0$為等式約束，對應的$h_i (x)$為等式約束函數。對於目標函數和約束函數來說，其有定義的點的集合的交集即為優化問題的定義域，表達式如式$$D=⋂_{i=0}^m\ dom\ f_i \ ∩\ ⋂_{i=1}^p\ dom\ h_i\]

所有可行點的集合稱為可行集或約束集。定義x^為優化問題的最優解，另外p^為優化問題的最優解的集合，此時P^定義為$$p^\ =\ inf⁡{f_0 (x) \ |\ f_0 (x)≤0,i=1,…,m, h_i (x)=0,i=1,…,p}.$$
在求解優化問題時，有時候並不需要得出精確的最優解，僅需接近最優解即可，因此滿足\(f_0 (x)≤p^*+ϵ，ϵ>0\)的可行解稱為\(ϵ-\)次優解，\(ϵ-\)次優解的集合稱為\(ϵ-\)次優集。
對於凸優化而言，相較於一般標准形式的優化問題，凸優化問題要求\(f_0 (x)\)為凸函數，\(f_i (x)\)也為凸函數，\(h_i (x)\)為仿射函數，其余相關概念與一般優化問題並無不同。因此凸優化問題的形式如下所示。

\[minimize\ f_0 (x)$$$$subject\ to\ f_i (x)≤0，i=1,…,m$$ $$h_i (x)=a_i^T x+b_i=0，i=1,…,p \]

4 拉格朗日對偶

4.1 Lagrangian函數

Lagrangian函數的基本思想是在目標函數中考慮一般優化問題的約束條件，即添加約束條件的加權和，得到增廣的目標函數。定義Lagrangian函數\(L:R^n×R^m×R^p→R\)為$$L(x,λ,ν)=f_0 (x)+∑_{i=1}^mλ_i f_i(x)+∑_{i=1}^pν_i h_i(x),$$
L函數的定義域為\(dom\ L=D×R^m×R^p\)，\(D\)集合定義由第3節已經給出。\(λ_i 、ν_i\)稱為拉格朗日乘子。

4.2 Lagrange對偶函數

有了Lagrangian函數后，可以定義Lagrange對偶函數\(g:R^m ×R^p→R\)為$$g(λ,ν)= inf_{x∈D}L(x,λ,ν)=inf_{x∈D}⁡\left(f_0 (x)+∑_{i=1}^mλ_i f_i(x)+∑_{i=1}^pν_i h_i(x)\right) ,$$
其中\(λ∈R^m，ν∈R^p\)，根據函數定義來看，其為Lagrange對偶函數關於\(x\)取最小值。因為對偶函數是一組關於\((λ,ν)\)的仿射函數的逐點下確界，所以即使如第3節中所述的標准形式優化問題並不是凸優化問題，其Lagrange對偶函數也是凹的，這一點值得關注。

4.3 對偶問題

對於任意一組\((λ,ν)\)，其中\(λ≽0\)，根據Lagrangian對偶函數的定義，其函數值為原優化問題的最優值\(p^*\)的一個下界。對於求出最大的下界，使其最為接近\(p^*\)這個問題可以表述為優化問題

\[maximize \ g(λ,ν)$$$$subject\ to \ λ≽0$$該優化問題就稱為對偶問題，設$d^*$為對偶問題的最優值，同樣的$λ^* 、ν^*$稱為最優拉格朗日乘子。$(p^*-d^*)$稱為對偶間隙，當$p^*=d^*$時稱為強對偶性，對應的$p^*≥d^*$稱為弱對偶性，因為$d^*$一定是$p^*$的某個下界，因此不存在$p^*<d^*$的情況。對於一般情況下的優化問題來說強對偶性並不成立，但是當優化問題是凸優化問題時，強對偶性通常（但不總是）成立。 #5 KKT條件 對於目標函數和約束函數可微的任意優化問題，如果其強對偶性成立，那么任何一對原問題最優解和對偶問題最優解必須滿足KKT條件。KKT條件共有5條，如下所示： $$f_i (x^* )≤0,\ i=1,…,m$$$$h_i (x^* )=0, \ i=1,…,p$$$$λ_i^*≥0, \ i=1,…,m$$$$λ_i^* f_i (x^* )=0, \ i=1,…,m$$$$∇f_0 (x^* )+∑_{i=1}^mλ_i^* ∇f_i (x^* )+∑_{i=1}^pν_i^* ∇h_i (x^* )=0\]

上述KKT條件中，第一條和第二條是原問題的可行性，第三條是對偶問題的可行性，第四條是互補松弛條件，第五條是穩定性條件。
對於非凸問題來說KKT條件僅僅是必要條件，而對於優化問題為凸問題來說KKT條件為充要條件。也因此對凸優化問題的算法設計基本均是圍繞KKT條件來進行的。

6 算法設計

本節中所涉及的無論是有約束還是無約束優化問題全為凸優化問題。
對於優化問題來說，任何的算法都是迭代的算法。在每個迭代算法中的每一次迭代均會有$$x^(k+1)=x^k+α^k d^k$$的計算。\(x^k\)表示第k時刻已經算出來的解。\(α^k\)表示步長，其為一維標量。\(d^k\)表示k時刻的方向，與\(x\)的維數相同。迭代算法主要是圍繞\(α^k\)和\(d^k\)的更新展開的。

6.1 下降方法

使用下降方法時，需要確保下降方向\(d^k\)已經確定。因此下降方法主要解決如何確定下降步長\(α^k\)的問題。

6.1.1 Amijo Rule法

Amijo Rule法是一種模糊的步長算法，也稱Back tracking方法。在該迭代算法中，若$$
f_0 (x^k+α^k d^k )>f_0 (x^k )+γα(∇f_0 (x^k ))^T d^k，$$則迭代繼續，否則停止。在該式中，每次迭代都由 \(α=αβ\) 來更新 \(α\) 的值。其中一般來說\(γ∈(0,0.5)，β∈(0,1)\)。\(γ\) 表示可以接受的f的減少量占基於線性外推預測的減少量的比值，正常取值在0.01到0.3之間。參數 \(β\) 的正常取值在0.1到0.8之間，\(β\) 取值越小搜索越粗糙。在計算時通常 \(α\) 的初始值會比較大，一般從1開始迭代。

6.1.2 黃金分割法

黃金分割法如圖所示。

 比較A、B兩點的函數值，若A大則將$α_min$更新為A點橫坐標，若B大則將$α_max$更新為B點橫坐標。如此重復迭代找出最優值。 ##6.2 無約束優化算法 根據第5節提出的KKT條件，對於無約束優化問題來說，KKT條件就被簡化成了$$∇f_0 (x^* )=0$$這一僅存的條件。因此求解無約束優化問題等價於求解 $n$ 個變量的 $n$ 個方程的線性方程組，特殊情況下可以通過直接求解上述KKT條件來獲得最優解，但是一般情況下必須采用迭代算法求解該KKT條件。 ###6.2.1 梯度下降法 梯度下降法即使用梯度的負方向作為搜索方向，即$d^(k+1)=-∇f(x^k)$。其步長$α^{k+1}$由6.1節中的介紹的下降方法或其他計算方法計算出來。下降方法的使用前提是需要首先知道下降方向，因此梯度下降算法的第一步是計算下降方向，第二步為通過下降方法計算步長，最終更新$x^{k+1}$的值。 梯度下降法的停止准則通常為$‖∇f(x)‖_2≤ε$，其中 $ε$ 是一個極小的正數。大部分情況下確定下降方向后就判斷迭代是否需要停止，而不是確定步長后判斷。 ###6.2.2 最速下降法 對$f(x+v)$在$x$出進行一階泰勒展開有$$f(x+v)≈f ̂(x+v)=f(x)+(∇f(x))^T v，$$運用在最速下降時，將式中的 $x$ 換成 $x^k$ 就有$$f(x^k+v)≈f ̂(x^k+v)=f(x^k )+(∇f(x^k ))^T v，$$下降方向$d^(k+1)$由式$$d^{k+1}=arg⁡min_v⁡\{f(x^k )+(∇f(x^k )^T )v \ |\ ‖v‖=1\}$$ 可得。對於$v$來說，可以選擇不同的范式來進行約束，同時得到的結果也不盡相同。當$‖v‖$為1范數時，則其方向為負梯度的沿坐標軸最大分量方向。當$‖v‖$為2范數時其與梯度下降法算出的下降方向類似，僅僅只是對其做了正則化。與梯度下降法類似，最速下降法也是首先找到最速下降方向，然后計算步長，最后更新$x^{k+1}$，直到滿足停止准則迭代停止。 ###6.2.3 坐標輪換法 很多時候計算梯度是比較麻煩的一件事，因此為了簡便，直接沿不同坐標方向輪換地進行搜索。輪換過程中每次允許一個變量變化，其余變量保持不變，在搜索的過程中可以不需要目標函數的導數，只需目標函數值信息。 設$x∈R^n$，則$d^k=e_{mod(k,n)}$，其中e表示單位向量，表示第$mod(k,n)$個元素為1。利用坐標輪換法計算出來的搜索方向不一定是下降方向，因此步長應該按搜索方向確定步長，即$-α_{max}≤α^k≤α_{max}$。 ###6.2.4 牛頓法/擬牛頓法 牛頓法中 $d^k=-(∇^2 f(x^k ))^{-1} ∇f(x^k )$ 為最優 $d^k$，即牛頓方向為當前點的Hessian矩陣的逆乘以負梯度的方向。對於牛頓法來說有以下算法流程：$$ (1)\ \ \ \ Repeat\ d^k=-(∇^2 f(x^k ))^{-1} ∇f(x^k )$$$$ α^k=arg min\{f(x^k+αd^k )\},0≤α≤α_{max}$$$$ x^{k+1}=x^k+α^k d^k$$$$(2)\ \ \ \ Until\ convergence\ or \left|(∇f(x^k ))^T (∇^2 f(x^k ))^{-1} ∇f(x^k )\right|≤ε$$ 牛頓法的優勢在於其收斂速度較梯度下降法、最速下降法快，對坐標選擇或者目標函數的下水平集不敏感，當問題規模比較大時與規模較小的問題性能相似，並不依賴於算法參數的選擇。但是牛頓法的最大缺點在於Hessian矩陣的計算與存儲成本較高，因此誕生了擬牛頓法。例如在擬牛頓法中的BFGS算法核心思想便是找到一個合適的矩陣 $B$ 來代替Hessian矩陣，以此簡化Hessian矩陣，實現更好的數值穩定性。 ##6.3 等式約束優化算法 僅具有等式約束的優化問題的KKT條件可以簡化為$$h_i (x^* )=0, i=1,…,p ，$$$$∇f_0 (x^* )+∑_{i=1}^pν_i^* ∇h_i (x^* )=0$$兩條。同時等式約束優化問題形式如$$minimize\ f_0 (x)$$$$subject\ to\ Ax=b$$ ###6.3.1 牛頓法 等式約束優化問題中的KKT條件若是非線性的，則將其進行泰勒二階展開使其線性化，因此牛頓法主要用來解決非線性的KKT條件問題。根據KKT條件的二階泰勒展開與等式約束的凸優化問題形式，其方向 $d^k$ 可由式$$ \begin{vmatrix}{∇^2 f(x^k)} & {A^T} \\ A& 0\\ \end{vmatrix} \begin{vmatrix}{d^k}\\ 0\\ \end{vmatrix} = \begin{vmatrix}{-∇^2 f(x^k)} \\ 0\\ \end{vmatrix}$$得。步長依然使用6.1節中介紹的方法或其他方法計算得出。 ###6.3.2 拉格朗日法 含等式約束的優化問題，且KKT條件非線性，也可以使用拉格朗日法來進行求解，但是拉格朗日法多用於理論分析研究，在實際運用中使用較少。拉格朗日法的求解如下所示：$$ \left \{ \begin{array}{l} x^{k+1}=x^k-α^k (∇f{x^k }+A^T v^k) \\ v^{k+1}=v^k+α^k (Ax^k-b) \end{array} \right. $$ ###6.3.3 增廣拉格朗日法 增廣拉格朗日法對等式約束優化問題更為有效。增廣拉格朗日函數形式如$$L_c (x,v)=f(x)+v^T (Ax-b)+c/2 ‖Ax-b‖_2^2$$ 所示。其中 $c>0$，$c$ 可以是常量也可以是變量。 增廣拉格朗日函數有兩個性質： **1**.若$v=v^*$，則對$∀c>0$來說均有$$x^*=arg min_x⁡L_c (x,v^*)$$ **2**.若$c→∞$，則對於$∀c$來說均有$$x^*=arg min_x⁡L_c (x,v)$$ 根據上述，可得增廣拉格朗日算法如下： $$x^{k+1}=arg min_x⁡L_c (x,v^k)⇔x^{k+1}=\frac{(c-v^k)}{(c+1)}$$ $$v^{k+1}=v^k+c(Ax^{k+1}-b)$$ ###6.3.4 交替方向法 假設有無約束優化問題min f(x)+g(x)，將其轉化為等式約束優化問題$$minimize\ \ \ \ f(x)+g(z)$$ $$subject\ to\ \ \ x=z$$ 那么其增廣拉格朗日函數就可以寫成 $$L_c (x,z,v)=f(x)+g(z)+v^T (x-z)+\frac c2 ‖x-z‖_2^2.$$ 依據6.3.3小節的拉格朗日法，有優化步驟： $$(1)\ \ \ \ \{x^{k+1},z^{k+1} \}=arg min_{x,z}⁡\left\{f(x)+g(z)+(v^k)^T (x-z)+\frac c2 ‖x-z‖_2^2 \right\}$$ $$(2)\ \ \ \ v^{k+1}=v^k+c(x^{k+1}-z^{k+1})$$ 將第一步分解為2步進行迭代 $$(1.a)\ \ \ \ x^{k+1\ |\ t+1}=arg min_x⁡\left\{f(x)+\frac c2 ‖x-z^{k+1\ |\ t}+\frac {v^k}c‖_2^2 \right\}$$ $$(1.b)\ \ \ \ z^{k+1\ |\ t+1}=arg min_z⁡ \left\{f(x)+\frac c2 ‖z-x^{k+1\ |\ t}-\frac {v^k}c‖_2^2 \right\}$$ 在優化步驟1中，若是用代碼來表示，則會有兩重循環，將其分解為兩個一重循環的方法即1.a和1.b稱為交替方向的拉格朗日乘子法。交替方向的拉格朗日乘子法在圖像處理、分布式計算中較為常用。 #7 總結 凸優化問題的求解均圍繞着KKT條件來進行，各式各樣的算法均有其適用的場合，並不存在優劣之說。當一個問題確定為凸優化問題后，往往比較容易被解決，最難的還是在於對實際問題進行數學建模，建立好有效的優化模型后，實際上問題就已經解決百分之八十。數學建模過程中，如何有效地根據實際問題、預估最優解來合理拋棄部分約束使問題簡單化才是優化問題的難點。 #8 參考文獻 Boyd,Stephen,and Lieven Vandenberghe.Convex optimization.Cambridge university press,2004.