
統計學基本知識
1、總體和樣本基本概念:
(1) 總體:表示研究對象的整個群體。
(2) 樣本:表示從總體中選取的一部分。
2、總體方差和樣本方差:
(1) 定義:
總體方差:總體方差是一組資料中各數值與其算術平均數離差平方和的平均數
公式為: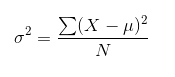
樣本方差:樣本方差是指構成樣本的隨機變量對離散中心 x之離差的平方和除以n-1,樣本方差用來表示一列數的變異程度
公式為:
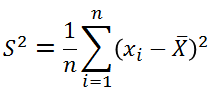
(2) 區別:總體方差是個確定值,樣本方差是個隨機變量
3、隨機變量:
隨機變量與普通變量不同,因為隨機變量通常是一個函數,用於量化隨機過程。通常用大寫字母X,Y,Z等表示,而傳統變量通常用小寫字母x,y,z表示。隨機變量有兩類:離散型和連續型。
4、泊松分布:
(1) 定義:泊松分布是一種統計與概率學里常見到的離散概率分布。
(2) 公式: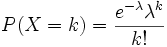
泊松分布P (λ)中只有一個參數λ ,它既是泊松分布的均值,也是泊松分布的方差。其中k=0,1,2…
正態分布

上面表達式中有兩個參數,即期望(均數)μ和標准差σ,σ2為方差
當μ = 0,σ = 1時的正態分布是標准正態分布。
大數定律
舉個例子: 投硬幣
一枚硬幣被拋出后有50%的可能為正面或者背面,在小樣本的情況下,隨機拋硬幣的結果可能並不明顯或者說結果沒有規律,不穩定等等,10次里可能有4次正面6次背面,也可能是7次正面3次背面,這很正常。但是隨着我們拋硬幣的次數的增多,正面和反面出現次數就會越來越接近於相同,也就是各趨近於50%。


