Python回歸分析五部曲（一）—簡單線性回歸

回歸最初是遺傳學中的一個名詞，是由英國生物學家兼統計學家高爾頓首先提出來的，他在研究人類身高的時候發現：高個子回歸人類的平均身高，而矮個子則從另一方向回歸人類的平均身高；

回歸分析整體邏輯

• 回歸分析（Regression Analysis）

  • 研究自變量與因變量之間關系形式的分析方法，它主要是通過建立因變量y與影響它的自變量 x_i(i=1,2,3… …)之間的回歸模型，來預測因變量y的發展趨向。

• 回歸分析的分類

  • 線性回歸分析

    • 簡單線性回歸
    • 多重線性回歸

  • 非線性回歸分析

    • 邏輯回歸
    • 神經網絡

• 回歸分析的步驟

  • 根據預測目標，確定自變量和因變量

  • 繪制散點圖，確定回歸模型類型

  • 估計模型參數，建立回歸模型

  • 對回歸模型進行檢驗

  • 利用回歸模型進行預測

簡單線性回歸模型

1.基礎邏輯

y=a+bx+e

該模型也稱作一元一次回歸方程，模型中：

• y：因變量
• x：自變量
• a：常數項（回歸直線在y軸上的截距）
• b：回歸系數（回歸直線的斜率）
• e：隨機誤差（隨機因素對因變量所產生的影響）
  
  • e的平方和也稱為殘差，殘差是判斷線性回歸擬合好壞的重要指標之一

從簡單線性回歸模型可以知道，簡單線性回歸是研究一個因變量與一個自變量間線性關系的方法

2.案例實操

下面我們來看一個案例，某金融公司在多次進行活動推廣后記錄了活動推廣費用及金融產品銷售額數據，如下表所示

因為活動推廣有明顯效果，現在的需求是投入60萬的推廣費，能得到多少的銷售額呢？這時我們就可以使用簡單線性回歸模型去解決這個問題，下面，我們用這個案例來學習，如何進行簡單線性回歸分析；

（1）第一步 確定變量

• 根據預測目標，確定自變量和因變量

  • 問題：投入60萬的推廣費，能夠帶來多少的銷售額？

  • 確定因變量和自變量很簡單，誰是已知，誰就是自變量，誰是未知，就就是因變量，因此，推廣費是自變量，銷售額是因變量；

import numpy
from pandas import read_csv
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression

data = read_csv( 'file:///Users/apple/Desktop/jacky_1.csv',encoding='GBK' )

（2）第二步 確定類型

• 繪制散點圖，確定回歸模型類型

  • 根據前面的數據，畫出自變量與因變量的散點圖，看看是否可以建立回歸方程，在簡單線性回歸分析中，我們只需要確定自變量與因變量的相關度為強相關性，即可確定可以建立簡單線性回歸方程，根據jacky前面的文章分享《Python相關分析》，我們很容易就求解出推廣費與銷售額之間的相關系數是0.94，也就是具有強相關性，從散點圖中也可以看出，二者是有明顯的線性相關的，也就是推廣費越大，銷售額也就越大

#畫出散點圖，求x和y的相關系數
plt.scatter(data.活動推廣費,data.銷售額)

data.corr()

（3）第三步 建立模型

• 估計模型參數，建立回歸模型
  

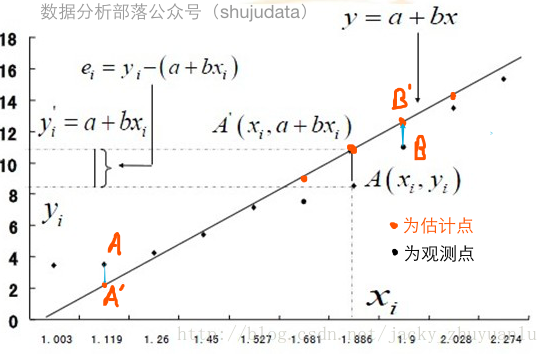
  要建立回歸模型，就要先估計出回歸模型的參數A和B，那么如何得到最佳的A和B，使得盡可能多的數據點落在或者更加靠近這條擬合出來的直線上呢？

統計學家研究出一個方法，就是最小二乘法，最小二乘法又稱最小平方法，通過最小化誤差的平方和尋找數據的最佳直線，這個誤差就是實際觀測點和估計點間的距離；

最小二乘法名字的緣由有二個：一是要將誤差最小化，二是使誤差最小化的方法是使誤差的平方和最小化；在古漢語中，平方稱為二乘，用平方的原因就是要規避負數對計算的影響，所以最小二乘法在回歸模型上的應用就是要使得實際觀測點和估計點的平方和達到最小，也就是上面所說的使得盡可能多的數據點落在或者說更加靠近這條擬合出來的直線上；

我們只要了解最小二乘法的原理即可，具體計算的過程就交給Python處理。


#估計模型參數，建立回歸模型
'''
(1) 首先導入簡單線性回歸的求解類LinearRegression
(2) 然后使用該類進行建模，得到lrModel的模型變量
'''

lrModel = LinearRegression()
#(3) 接着，我們把自變量和因變量選擇出來
x = data[['活動推廣費']]
y = data[['銷售額']]

#模型訓練
'''
調用模型的fit方法，對模型進行訓練
這個訓練過程就是參數求解的過程
並對模型進行擬合
'''
lrModel.fit(x,y)

（4）第四步 模型檢驗

• 對回歸模型進行檢驗

  • 回歸方程的精度就是用來表示實際觀測點和回歸方程的擬合程度的指標，使用判定系數來度量。

判定系數＝相關系數R2=ESSTSS=1−RSSTSS

其中，數據分析部落公眾號(shujudata)

TSS=∑(Yi−Y¯)2總離差平方和

ESS=∑(Yi−Y¯)2回歸差平方和

RSS=∑(Yi−Y¯)2殘差平方和

解釋：判定系數等於相關系數R的平方用於表示擬合得到的模型能解釋因變量變化的百分比，R平方越接近於1，表示回歸模型擬合效果越好
如果擬合出來的回歸模型精度符合我們的要求，那么我們可以使用擬合出來的回歸模型，根據已有的自變量數據來預測需要的因變量對應的結果

#對回歸模型進行檢驗
lrModel.score(x,y)

執行代碼可以看到，模型的評分為0.887,是非常不錯的一個評分，我們就可以使用這個模型進行未知數據的預測了

（5）第五步 模型預測

• 調用模型的predict方法，這個就是使用sklearn進行簡單線性回歸的求解過程；

lrModel.predict([[60],[70]])

• 如果需要獲取到擬合出來的參數各是多少，可以使用模型的intercept屬性查看參數a(截距)，使用coef屬性查看參數b

#查看截距
alpha = lrModel.intercept_[0]

#查看參數
beta = lrModel.coef_[0][0]

alpha + beta*numpy.array([60,70])

3.完整代碼

import numpy
from pandas import read_csv
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression

data = read_csv(
    'file:///Users/apple/Desktop/jacky_1.csv',encoding='GBK'
)

#畫出散點圖，求x和y的相關系數
plt.scatter(data.活動推廣費,data.銷售額)

data.corr()

#估計模型參數，建立回歸模型
''' (1) 首先導入簡單線性回歸的求解類LinearRegression (2) 然后使用該類進行建模，得到lrModel的模型變量 '''

lrModel = LinearRegression()
#(3) 接着，我們把自變量和因變量選擇出來
x = data[['活動推廣費']]
y = data[['銷售額']]

#模型訓練
''' 調用模型的fit方法，對模型進行訓練 這個訓練過程就是參數求解的過程 並對模型進行擬合 '''
lrModel.fit(x,y)

#對回歸模型進行檢驗
lrModel.score(x,y)

#利用回歸模型進行預測
lrModel.predict([[60],[70]])

#查看截距
alpha = lrModel.intercept_[0]

#查看參數
beta = lrModel.coef_[0][0]

alpha + beta*numpy.array([60,70])

4.總結-sklearn建模流程

• sklearn建模流程

  • 建立模型

    • lrModel = sklearn.linear_model.LinearRegression()

  • 訓練模型

    • lrModel.fit(x,y)

  • 模型評估

    • lrModel.score(x,y)

  • 模型預測

    • lrModel.predict(x)