原文鏈接: http://tecdat.cn/?p=4612
貝葉斯分析的許多介紹使用相對簡單的教學實例 。雖然這可以很好地介紹貝葉斯原理,但將這些原則擴展到回歸並不是直截了當的。
這篇文章將概述這些原則如何擴展到簡單的線性回歸。在此過程中,我將推導出感興趣的參數的后驗條件分布,呈現用於實現Gibbs采樣器的R代碼,並呈現所謂的網格點方法。
貝葉斯模型
假設我們觀察到的數據
有興趣的是推斷
假設超參數
括號中的術語是數據或可能性的聯合分布。其他術語包括參數的聯合先驗分布(因為我們隱含地假定先前獨立,聯合先前因子)。
這被認為是熟悉的表達方式:
隨附的R代碼的第0部分從該模型生成用於指定“真實”參數的數據。我們稍后將使用此數據估計貝葉斯回歸模型,以檢查我們是否可以恢復這些真實參數。
Gibbs采樣器
從這個后驗分布中得出,我們可以使用吉布斯采樣算法。吉布斯采樣是一種迭代算法,它根據每個感興趣參數的后驗分布產生樣本。它是通過以下列方式從每個參數的條件后驗順序繪制來實現的:
可以證明,在適當的老化期后,1000次抽取的剩余部分是從后部分布中抽出的。這些樣本不是獨立的。繪制的順序是在后部空間中的隨機游走,並且空間中的每個步驟取決於先前的位置。通常也會使用稀疏期(這里沒有這樣做)。減薄10意味着我們每10次抽獎。這個想法是,每一個平局可能依賴於以前的平局,但不能 作為依賴於10日以前的平局。
條件后驗分布
要使用Gibbs,我們需要確定每個參數的條件后驗。
它有助於從完全非標准化的后驗開始:
為了找到參數的條件后驗,我們簡單地從不包括該參數的聯合后驗中刪除所有項。例如,常數項
同樣的,
條件后驗可以被識別為另一個反伽馬分布,具有一些代數操作。
的條件后驗
網格方法
考慮
然后在每個網格點評估的條件后驗分布告訴我們該抽取的相對可能性。
然后我們可以使用R中的sample()函數從這些點網格中繪制,采樣概率與網格點處的密度評估成比例。
這在隨附的R代碼的第1部分中的函數rb0cond()和rb1cond()中實現。
在使用網格方法時遇到數值問題是很常見的。由於我們正在評估網格上的非標准化后驗,因此結果會變得相當大或很小。這可能會在R中產生Inf和-Inf值。
例如,在函數rb0cond()和rb1cond()中,我實際上計算了導出的條件后驗分布的對數。然后,我從所有評估的最大值中減去每個評估,然后從對數標度中取代,然后進行標准化。這傾向於處理這樣的數字問題。
我們不需要使用網格方法從條件后驗中繪制,
請注意,此網格方法有一些缺點。
首先,它的計算成本很高。如我們所做的那樣,通過代數並希望得到一個已知的后驗分布可以在計算上更有效率
其次,網格方法需要指定網格點的區域。如果條件后驗在我們指定的[-10,10]的網格區間之外有明顯的密度怎么辦?在這種情況下,我們不會從條件后驗得到准確的樣本。記住這一點並嘗試寬網格間隔非常重要。因此,我們需要聰明地處理數值問題,例如接近Inf的數字和R中的-Inf值。
仿真結果
現在我們可以從每個參數的條件后驗中進行采樣,我們可以實現Gibbs采樣器。這在隨附的R代碼的第2部分中完成。它編碼上面R中概述的相同算法。
結果很好。下圖顯示了1000個Gibbs樣本的序列(刪除了老化抽取並且未實施細化)。紅線表示我們模擬數據的真實參數值。第四個圖顯示了截距和斜率項的聯合后驗,紅線表示輪廓。
總而言之,我們首先導出了一個表達式,用於參數的聯合分布。然后我們概述了用於從后部繪制樣本的Gibbs算法。在這個過程中,我們認識到Gibbs方法依賴於每個參數的條件后驗分布的順序繪制。因為



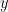








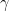
![p(\ beta_0,\ beta_1,\ phi | \ vec y)\ propto \ Big [\ prod_ {i = 1} ^ np(y_i | \ beta_0,\ beta_1,\ phi)\ Big] p(\ beta_0 | \ mu_0,\ tau_0)p(\ beta_1 | \ mu_1,\ tau_1)p(\ phi | \ alpha,\ gamma)](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PXAlMjglNUNiZXRhXzAlMkMrJTVDYmV0YV8xJTJDKyU1Q3BoaSslN0MrJTVDdmVjK3klMjkrJTVDcHJvcHRvKyU1Q0JpZyslNUIlNUNwcm9kXyU3QmklM0QxJTdEJTVFbitwJTI4eV9pKyU3QyslNUNiZXRhXzAlMkMrJTVDYmV0YV8xJTJDKyU1Q3BoaSslMjklNUNCaWclNUQrcCUyOCslNUNiZXRhXzArJTdDKyU1Q211XzAlMkMrJTVDdGF1XzArJTI5K3AlMjglNUNiZXRhXzErJTdDKyU1Q211XzElMkMrJTVDdGF1XzElMjkrcCUyOCslNUNwaGkrJTdDKyU1Q2FscGhhJTJDKyU1Q2dhbW1hJTI5KyZiZz1mZmZmZmYmZmc9MDAwMDAwJnM9MA==.png)





![\ begin {aligned} p(\ phi | \ beta_0,\ beta_1,\ alpha,\ gamma,\ vec y)&\ propto \ phi ^ { - n / 2} \ phi ^ { - (\ alpha + 1)e ^ { - \ frac {\ gamma} {\ phi}}} e ^ { - \ frac {1} {2 \ phi} \ sum_ {i = 1} ^ {n}(y_i - (\ beta_0 + \ beta_1x_i) )^ 2} \\&= \ phi ^ { - (\ alpha + \ frac {n} {2} + 1)} exp { - \ frac {1} {\ phi} \ Big [\ frac {1} { 2 \ phi} \ sum_ {i = 1} ^ {n}(y_i - (\ beta_0 + \ beta_1x_i))^ 2 + \ gamma \ Big]} \\&= IG(shape = \ alpha + \ frac {n } {2},\ rate = \ frac {1} {2 \ phi} \ sum_ {i = 1} ^ {n}(y_i - (\ beta_0 + \ beta_1x_i))^ 2 + \ gamma)\ end {aligned }](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PSU1Q2JlZ2luJTdCYWxpZ25lZCU3RCtwJTI4JTVDcGhpKyU3QyslNUNiZXRhXzAlMkMrJTVDYmV0YV8xJTJDKyU1Q2FscGhhJTJDKyU1Q2dhbW1hJTJDKyU1Q3ZlYyt5JTI5KyUyNislNUNwcm9wdG8rJTVDcGhpJTVFJTdCLW4lMkYyJTdEKyU1Q3BoaSU1RSU3Qi0lMjglNUNhbHBoYSslMkIrMSUyOStlJTVFJTdCLSU1Q2ZyYWMlN0IlNUNnYW1tYSU3RCU3QiU1Q3BoaSU3RCU3RCU3RCtlJTVFJTdCLSU1Q2ZyYWMlN0IxJTdEJTdCMiU1Q3BoaSU3RCslNUNzdW1fJTdCaSUzRDElN0QlNUUlN0JuJTdEJTI4eV9pKy0rJTI4JTVDYmV0YV8wKyUyQislNUNiZXRhXzF4X2klMjkrJTI5JTVFMiU3RCslNUMlNUMrJTI2KyUzRCslNUNwaGklNUUlN0ItJTI4JTVDYWxwaGErJTJCKyU1Q2ZyYWMlN0JuJTdEJTdCMiU3RCslMkIrMSUyOSU3RCtleHAlN0ItJTVDZnJhYyU3QjElN0QlN0IlNUNwaGklN0QrJTVDQmlnJTVCKyU1Q2ZyYWMlN0IxJTdEJTdCMiU1Q3BoaSU3RCslNUNzdW1fJTdCaSUzRDElN0QlNUUlN0JuJTdEJTI4eV9pKy0rJTI4JTVDYmV0YV8wKyUyQislNUNiZXRhXzF4X2klMjkrJTI5JTVFMislMkIrJTVDZ2FtbWErJTVDQmlnJTVEKyU3RCslNUMlNUMrJTI2KyUzRCtJRyUyOHNoYXBlKyUzRCslNUNhbHBoYSslMkIrJTVDZnJhYyU3Qm4lN0QlN0IyJTdEJTJDKyU1QytyYXRlKyUzRCslNUNmcmFjJTdCMSU3RCU3QjIlNUNwaGklN0QrJTVDc3VtXyU3QmklM0QxJTdEJTVFJTdCbiU3RCUyOHlfaSstKyUyOCU1Q2JldGFfMCslMkIrJTVDYmV0YV8xeF9pJTI5KyUyOSU1RTIrJTJCKyU1Q2dhbW1hKyUyOSslNUNlbmQlN0JhbGlnbmVkJTdEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png)