機器學習——XGBoost

###基礎概念 XGBoost（eXtreme Gradient Boosting）是GradientBoosting算法的一個優化的版本，針對傳統GBDT算法做了很多細節改進，包括損失函數、正則化、切分點查找算法優化等。
####xgboost的優化點

• 相對於傳統的GBM，XGBoost增加了正則化步驟。正則化的作用是減少過擬合現象。

• xgboost可以使用隨機抽取特征，這個方法借鑒了隨機森林的建模特點，可以防止過擬合。

• 速度上有很好的優化，主要體現在以下方面：
  1、現了分裂點尋找近似算法，先通過直方圖算法獲得候選分割點的分布情況，然后根據候選分割點將連續的特征信息映射到不同的buckets中，並統計匯總信息。
  2、xgboost考慮了訓練數據為稀疏值的情況，可以為缺失值或者指定的值指定分支的默認方向，這能大大提升算法的效率。
  3、正常情況下Gradient Boosting算法都是順序執行，所以速度較慢，xgboost特征列排序后以塊的形式存儲在內存中，在迭代中可以重復使用,因而xgboost在處理每個特征列時可以做到並行。

總的來說，xgboost相對於GBDT在模型訓練速度以及在降低過擬合上不少的提升。

###XGBOOST原理

基於不同y的理解, 我們可以有不同的問題,如回歸、分類、排序等。 我們需要找到一種方法來找到最好的參數給定的訓練數據。 為了達到這個目的,我們需要定義一個 目標函數 , 用它來測量模型的性能。目標函數包含兩部分：損失函數+正則項

其中L為損失函數，Ω是正則項，在預測數據時常用的損失函數比如均方根誤差：

另外一個常用的損失函數是logistic損失函數：

其中，我們是通關不斷優化，降低損失函數，來提高模型的性能，另外，正則項的主要作用是防止模型的過擬合現象。

對於xgboost而言，它的目標函數可以寫成：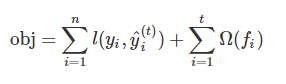 

xgboost比傳統解決最優化問題常用的梯度迭代方法要跟難，它並不是一次性訓練所有樹，而是采用一種加法策略，一次添加一個樹，因此步驟t的預測值y可以寫：

根據上面的推理過程，我們可以把目標函數寫成：

如果考慮使用均方誤差作為損失函數的，最終可以使用的目標函數可寫成

對以上目標函數進行二階泰勒展開，得到以下公式：

其中，gi和hi被定義為：

最終的目標函數表示形式為：

從中可以看到，xgboost的最優化問題，將取決於目標函數過程中gi和hi取值。

###補充理解 補充理解部分主要是對上面提到的正則化和泰勒展開式做補充解釋
####泰勒展開式

泰勒公式是一個用函數在某點的信息描述其附近取值的公式。如果函數足夠平滑的話，在已知函數在某一點的各階導數值的情況之下，泰勒公式可以用這些導數值做系數構建一個多項式來近似函數在這一點的鄰域中的值。泰勒公式還給出了這個多項式和實際的函數值之間的偏差。

在機器學習中，使用泰勒展開式的目的是通過泰勒展開式函數的局部近似特性來簡化復雜函數的表達。

例如：
函數y=x^3，當自變量有變化時，即 △x，自變量y會變化△y,帶入到函數里面就有:

當△x —> 0時，上式的后兩項是△x的高階無窮小舍去的話上式就變成了

也就是說當自變量x足夠小的時候，也就是在某點的很小的鄰域內，Δy是可以表示成Δx的線性函數的。線性函數計算起來，求導起來會很方便。
對於一般函數，當在某點很小領域內我們也可以寫成類似上面的這種自變量和因變量之間線性關系

變化一下形式Δy=f(x)-f(x0), Δx = x-x0在代入上式

這個就是在x0點鄰域內舍掉高階無窮小項以后得到的局部線性近似公式了。為了提高近似的精確度，於是把上面的一次近似多項式修正為二次多項式。再進一步二次修正為三次，一直下去就得到n階泰勒多項式。

只做一次近似的公式如下：

近似的多項式和原始函數是通過同一點x0。

進行二次近似的公式如下：

近似的多項式和原始函數既過同一點，而且在同一點的導數相同，也就是多項式表達的函數在x0點的切線也相同。

最終n階泰勒展開公式：

展開越多近似程度越高。

####L1正則化和L2正則化 L1正則化和L2正則化可以看做是損失函數的懲罰項。所謂『懲罰』是指對損失函數中的某些參數做一些限制。對於線性回歸模型，使用L1正則化的模型建叫做Lasso回歸，使用L2正則化的模型叫做Ridge回歸（嶺回歸）。

通常情況下，L1正則化是在損失函數上加入一項α||w||₁，L2正則化則是在損失函數上加入一項α||w||₂²

一般回歸分析中回歸w表示特征的系數，從上式可以看到正則化項是對系數做了處理（限制）。L1正則化和L2正則化的說明如下：

• L1正則化是指權值向量w中各個元素的絕對值之和，通常表示為||w||₁，L1正則化可以產生稀疏權值矩陣，即產生一個稀疏模型，可以用於特征選擇。
• L2正則化是指權值向量w中各個元素的平方和然后再求平方根，通常表示為||w||₂，L2正則化可以防止模型過擬合（overfitting）；一定程度上，L1也可以防止過擬合。

####L1正則化的作用闡述 L1正則化有助於生成一個稀疏權值矩陣（稀疏矩陣指的是很多元素為0，只有少數元素是非零值的矩陣，即得到的線性回歸模型的大部分系數都是0. ），進而可以用於特征選擇。

通常機器學習中特征數量很多，例如文本處理時，如果將一個詞組（term）作為一個特征，那么特征數量會達到上萬個（bigram）。在預測或分類時，那么多特征顯然難以選擇，但是如果代入這些特征得到的模型是一個稀疏模型，表示只有少數特征對這個模型有貢獻，絕大部分特征是沒有貢獻的，或者貢獻微小（因為它們前面的系數是0或者是很小的值，即使去掉對模型也沒有什么影響），此時我們就可以只關注系數是非零值的特征。這就是稀疏模型與特征選擇的關系。

####L2正則化的作用闡述 L2正則化可以在擬合過程構造一個所有參數都比較小的模型。因為一般認為參數值小的模型比較簡單，能適應不同的數據集，也在一定程度上避免了過擬合現象。可以設想一下對於一個線性回歸方程，若參數很大，那么只要數據偏移一點點，就會對結果造成很大的影響；但如果參數足夠小，數據偏移得多一點也不會對結果造成什么影響，專業一點的說法是抗擾動能力強。
###python中xgboost的使用

xgboost的參數可以分為三類：通用參數，booster參數及目標參數。


1、通用參數

• booster:選擇基分類器，可選參數gbtree和gblinear，默認為gbtree
• silent:是否打印模型信息，0表示打印，1表示不打印，默認0
• nthread:線程數選擇，默認為最大可用線程數
• num_pbuffer：預測緩沖區的大小,通常設置為訓練實例的數量。緩沖區用於保存最后的預測結果提高一步
• num_feature：boosting過程中用到的特征維數，一般xgboost會自動設置

2、booster參數 * eta ：學習步長，相當於其他集合模型中的learning_rate,默認為0.3，一般范圍0.01-0.2 * gamma：最小損失函數值，默認為0，對於一個節點的划分只有在其loss function 得到結果大於0的情況下才進行 * max_depth：樹的最大深度，默認為6 ，用於控制過擬合 * min_child_weight：子節點最小的樣本權重，默認為1，用於控制過擬合 * max_delta_step：每棵樹權重改變的最大步長，默認為0，一般不設置 * subsample：隨機采樣的比例，默認為1，用戶控制過擬合 * colsample_bytree：隨機抽取特征比例，默認1，用戶控制過擬合 * colsample_bylevel：每個層級隨機抽取特征比例，默認為1 * lambda：l2正則項參數，默認為1 * alpha：l1正則項參數，默認為1 * tree_method：樹的構造方法，默認為auto auto 啟發式方法 exact 精確貪婪算法 approx 近似貪婪算法 hist 垂直最優化貪婪算法 * scale_pos_weight：類別處理不平衡處理，默認為0，大於0的取值可以處理類別不平衡的問題。幫助模型更快收斂 * updater 更新樹的構建方法, * refresh_leaf 節點更新，默認為true * process_type boosting處理方式選擇，默認為default * max_leaves 樹的最大節點數增加，默認為0
3、目標參數 * objective：損失函數選擇，默認為reg:linear，可選參數如下 “reg:linear” –線性回歸。 “reg:logistic” –邏輯回歸。 “binary:logistic” –二分類的邏輯回歸問題，輸出為概率。 “binary:logitraw” –二分類的邏輯回歸問題，輸出的結果為wTx。 “count:poisson” –計數問題的poisson回歸，輸出結果為poisson分布。在poisson回歸中，max_delta_step的缺省值為0.7。(used to safeguard optimization) “multi:softmax” –讓XGBoost采用softmax目標函數處理多分類問題，同時需要設置參數num_class（類別個數） “multi:softprob” –和softmax一樣，但是輸出的是ndata * nclass的向量，可以將該向量reshape成ndata行nclass列的矩陣。每行數據表示樣本所屬於每個類別的概率。 “rank:pairwise” –通過最小化pairwise損失做排名任務

• eval_metric：最優化損失函數的方法
  rmse 均方根誤差
  mae 平均絕對誤差
  logloss 負對數似然函數值
  error 二分類錯誤率
  merror 多分類錯誤率
  mlogloss 多分類logloss損失函數
  auc 曲線下面積排名估計
  ndcg 歸一化累積增益

###python代碼實現

import xgboost as xgb
from sklearn.datasets import load_boston
import pandas as pd
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score


boston = load_boston()
#查看波士頓數據集的keys
print(boston.keys())
boston_data=boston.data
target_var=boston.target
feature=boston.feature_names

boston_df=pd.DataFrame(boston_data,columns=boston.feature_names)
boston_df['tar_name']=target_var

#查看目標變量描述統計
print(boston_df['tar_name'].describe())
#把數據集轉變為二分類數據
boston_df.loc[boston_df['tar_name']<=21,'tar_name']=0
boston_df.loc[boston_df['tar_name']>21,'tar_name']=1


x_train, x_test, y_train, y_test = train_test_split(boston_df[feature], boston_df['tar_name'], test_size=0.30, random_state=1)

train_data=xgb.DMatrix(x_train,label=y_train)
dtrain=xgb.DMatrix(x_train)
dtest=xgb.DMatrix(x_test)

params={'booster':'gbtree',
    'objective': 'binary:logistic',
    'eval_metric': 'auc',
    'max_depth':6,
    'subsample':0.75,
    'colsample_bytree':0.75,
    'eta': 0.03,}

watchlist = [(train_data,'train')]
bst=xgb.train(params,train_data,num_boost_round=100,evals=watchlist)


# 度量xgboost的准確性
y_train_pred = (bst.predict(dtrain)>=0.5)*1
y_test_pred =(bst.predict(dtest)>=0.5)*1
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('xgboost train/test accuracies %.3f/%.3f' % (tree_train, tree_test))

結果為：xgboost train/test accuracies 0.980/0.868

參考資料：http://xgboost.readthedocs.io/en/latest/model.html