原文地址： http://xgboost.apachecn.org/cn/latest/model.html#xgboost 

Boosted Trees 介紹

XGBoost 是 “Extreme Gradient Boosting” 的縮寫，其中 “Gradient Boosting” 一詞在論文 Greedy Function Approximation: A Gradient Boosting Machine 中，由 Friedman 提出。 XGBoost 基於這個原始模型。 這是 gradient boosted trees（梯度增強樹）的教程，大部分內容是基於 xgboost 的作者的這些 slides 。

GBM （boosted trees，增強樹）已經有一段時間了，關於這個話題有很多的材料。 這個教程試圖用監督學習的元素以獨立和有原則的方式解釋 boosted trees （增強樹）。 我們認為這個解釋更加清晰，更加正式，並激發了 xgboost 中使用的變體。

監督學習的要素

XGBoost 用於監督學習問題，我們使用訓練數據 xixi 來預測目標變量 yiyi 。 在我們深入了解 boosted trees 之前，首先回顧一下監督學習的重要組成部件。

模型和參數

監督學習中的 model（模型） 通常是指給定輸入 xixi 如何去預測輸出 yiyi 的數學結構。 例如，一個常見的模型是一個 linear model（線性模型）（如線性回歸和 logistic regression），其中的預測是由 y^i=∑jwjxijy^i=∑jwjxij 給出的，這是加權輸入特征的線性組合（線性疊加的方式）。 其實這里的預測 yy 可以有不同的解釋，取決於做的任務。 例如，我們可以通過 logistic 轉換得到 logistic regression 中 positive 類別的概率，當我們想要對輸出結果排序的時候，也可以作為排序得分指標等。

parameters（參數） 是我們需要從數據中學習的未確定部分。在線性回歸問題中，參數是系數 ww 。 通常我們使用 ΘΘ 來表示參數。

目標函數：訓練損失 + 正則

基於對 yiyi 的不同理解，我們可以得到不同的問題，比如回歸，分類，排序等。 我們需要找到一種方法來找到訓練數據的最佳參數。為了做到這一點，我們需要定義一個所謂的 objective function（目標函數） 以給定一組參數來衡量模型的性能。

關於目標函數的一個非常重要的事實是，它們 must always（必須總是） 包含兩個部分：training loss （訓練損失） 和 regularization（正則化）。

Obj(Θ)=L(Θ)+Ω(Θ)Obj(Θ)=L(Θ)+Ω(Θ)

其中 LL 是訓練損失函數， ΩΩ 是正則化項。 training loss （訓練損失）衡量我們的數據對訓練數據的預測性。 例如，常用的訓練損失是 mean squared error（均方誤差，MSE）。

L(Θ)=∑i(yi−y^i)2L(Θ)=∑i(yi−y^i)2

另一個常用的損失函數是 logistic 回歸的 logistic 損失。

L(θ)=∑i[yiln(1+e−y^i)+(1−yi)ln(1+ey^i)]L(θ)=∑i[yiln⁡(1+e−y^i)+(1−yi)ln⁡(1+ey^i)]

regularization term（正則化項） 是人們通常忘記添加的內容。正則化項控制模型的復雜性，這有助於避免過擬合。 這聽起來有些抽象，那么我們在下面的圖片中考慮下面的問題。在圖像左上角給出輸入數據點的情況下，要求您在視覺上 fit（擬合） 一個 step function（階梯函數）。 您認為三種中的哪一種解決方案是最擬合效果最好的？

答案已經標注為紅色了。請思考一下這個是否在你的視覺上較為合理？總的原則是我們想要一個 simple（簡單） 和 predictive（可預測） 的模型。 兩者之間的權衡也被稱為機器學習中的 bias-variance tradeoff（偏差-方差 權衡）。

對於線性模型常見的正則化項有 L2L2 正則和 L1L1 正則。這樣的目標函數的設計來自於統計學習中的一個重要概念，也是我們剛才說的， bias-variance tradeoff（偏差-方差 權衡）。比較感性的理解， Bias 可以理解為假設我們有無限多數據的時候，可以訓練出最好的模型所拿到的誤差。而 Variance 是因為我們只有有限數據，其中隨機性帶來的誤差。目標中誤差函數鼓勵我們的模型盡可能去擬合訓練數據，這樣相對來說最后的模型會有比較小的 bias 。而正則化項則鼓勵更加簡單的模型。因為當模型簡單之后，有限數據擬合出來結果的隨機性比較小，不容易過擬合，使得最后模型的預測更加穩定。

為什么要介紹 general principle（一般原則）

上面介紹的要素構成了監督學習的基本要素，它們自然是機器學習工具包的基石。 例如，你應該能夠描述 boosted trees 和 random forests 之間的差異和共同點。 以正式的方式理解這個過程也有助於我們理解我們正在學習的目標以及啟發式算法背后的原因，例如 pruning 和 smoothing 。

tree ensembles（樹集成）

既然我們已經介紹了監督學習的內容，那么接下來讓我們開始介紹真正的 trees 吧。 首先，讓我們先來了解一下 xgboost 的 model（模型） ： tree ensembles（樹集成）。 樹集成模型是一組 classification and regression trees （CART）。 下面是一個 CART 的簡單的示例，它可以分類是否有人喜歡電腦游戲。

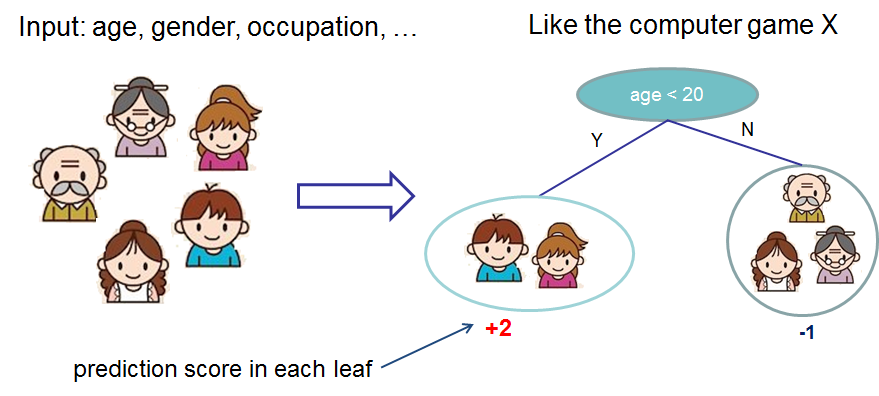
我們把一個家庭的成員分成不同的葉子，並把他們分配到相應的葉子節點上。 CART 與 decision trees（決策樹）有些許的不同，就是葉子只包含決策值。在 CART 中，每個葉子都有一個 real score （真實的分數），這給了我們更豐富的解釋，超越了分類。 這也使得統一的優化步驟更容易，我們將在本教程的后面部分看到。

通常情況下，單棵樹由於過於簡單而不夠強大到可以支持在實踐中使用的。實際使用的是所謂的 tree ensemble model（樹集成模型），它將多棵樹的預測加到一起。

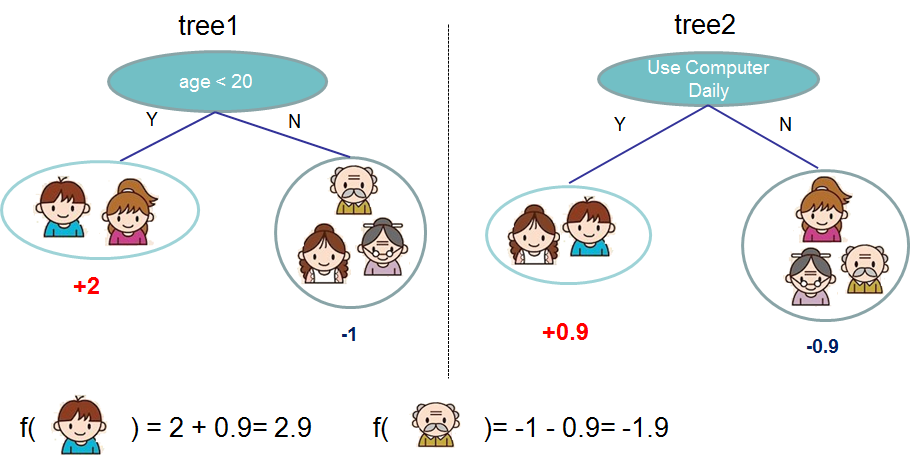
上圖是兩棵樹的集成的例子。將每棵樹的預測分數加起來得到最終分數。 如果你看一下這個例子，一個重要的事實就是兩棵樹互相 complement（補充） 。 在數學表示上，我們可以在表單中編寫我們的模型。

y^i=∑k=1Kfk(xi),fk∈Fy^i=∑k=1Kfk(xi),fk∈F

其中 KK 是樹的數量， ff 是函數空間 FF 的函數， FF 是所有可能的 CARTs 的集合。所以我們優化的目標可以寫成

obj(Θ)=∑inl(yi,y^i)+∑k=1KΩ(fk)obj(Θ)=∑inl(yi,y^i)+∑k=1KΩ(fk)

那么問題來了，random forests（隨機森林）的 model（模型） 是什么？這正是 tree ensembles（樹集成）！所以 random forests 和 boosted trees 在模型上並沒有什么不同，不同之處在於我們如何訓練它們。這意味着如果你寫一個 tree ensembles（樹集成）的預測服務，你只需要編寫它們中的一個，它們應該直接為 random forests（隨機森林）和 boosted trees（增強樹）工作。這也是監督學習基石元素的一個例子。

Tree Boosting

在介紹完模型之后，我們從真正的訓練部分開始。我們應該怎么學習 trees 呢？ 答案是，對於所有的監督學習模型都一樣的處理：定義一個合理的目標函數，然后去嘗試優化它！

假設我們有以下目標函數（記住它總是需要包含訓練損失和正則化）

Obj=∑i=1nl(yi,y^(t)i)+∑i=1tΩ(fi)Obj=∑i=1nl(yi,y^i(t))+∑i=1tΩ(fi)

附加訓練

我們想要問的第一件事就是樹的 parameters（參數） 是什么。 你可能已經發現了，我們要學習的是那些函數 fifi ，每個函數都包含樹的結構和葉子分數。這比傳統的你可以找到捷徑的優化問題要難得多。在 tree ensemble 中，參數對應了樹的結構，以及每個葉子節點上面的預測分數。 一次性訓練所有的樹並不容易。 相反，我們使用一個附加的策略：優化好我們已經學習完成的樹，然后一次添加一棵新的樹。 我們通過 y^(t)iy^i(t) 來關注步驟 tt 的預測值，所以我們有

y^(0)iy^(1)iy^(2)iy^(t)i=0=f1(xi)=y^(0)i+f1(xi)=f1(xi)+f2(xi)=y^(1)i+f2(xi)…=∑k=1tfk(xi)=y^(t−1)i+ft(xi)y^i(0)=0y^i(1)=f1(xi)=y^i(0)+f1(xi)y^i(2)=f1(xi)+f2(xi)=y^i(1)+f2(xi)…y^i(t)=∑k=1tfk(xi)=y^i(t−1)+ft(xi)

另外還有一個問題，每一步我們想要哪棵 tree 呢？一個自然而然的事情就是添加一個優化我們目標的方法。

Obj(t)=∑i=1nl(yi,y^(t)i)+∑i=1tΩ(fi)=∑i=1nl(yi,y^(t−1)i+ft(xi))+Ω(ft)+constantObj(t)=∑i=1nl(yi,y^i(t))+∑i=1tΩ(fi)=∑i=1nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+constant

如果我們考慮使用 MSE 作為我們的損失函數，它將是下面的形式。

Obj(t)=∑i=1n(yi−(y^(t−1)i+ft(xi)))2+∑i=1tΩ(fi)=∑i=1n[2(y^(t−1)i−yi)ft(xi)+ft(xi)2]+Ω(ft)+constantObj(t)=∑i=1n(yi−(y^i(t−1)+ft(xi)))2+∑i=1tΩ(fi)=∑i=1n[2(y^i(t−1)−yi)ft(xi)+ft(xi)2]+Ω(ft)+constant

MSE 的形式比較友好，具有一階項（通常稱為殘差）和二次項。 對於其他形式的損失（例如，logistic loss），獲得這么好的形式並不是那么容易。 所以在一般情況下，我們把損失函數的泰勒展開到二階

Obj(t)=∑i=1n[l(yi,y^(t−1)i)+gift(xi)+12hif2t(xi)]+Ω(ft)+constantObj(t)=∑i=1n[l(yi,y^i(t−1))+gift(xi)+12hift2(xi)]+Ω(ft)+constant

其中 gigi 和 hihi 被定義為

gihi=∂y^(t−1)il(yi,y^(t−1)i)=∂2y^(t−1)il(yi,y^(t−1)i)gi=∂y^i(t−1)l(yi,y^i(t−1))hi=∂y^i(t−1)2l(yi,y^i(t−1))

我們刪除了所有的常量之后， tt 步驟中的具體目標就變成了

∑i=1n[gift(xi)+12hif2t(xi)]+Ω(ft)∑i=1n[gift(xi)+12hift2(xi)]+Ω(ft)

這成為了新樹的優化目標。這個定義的一個重要優點是它只依賴於 gigi 和 hihi 。這就是 xgboost 如何支持自定義損失函數。 我們可以使用完全相同的使用 gigi 和 hihi 作為輸入的 solver（求解器）來對每個損失函數進行優化，包括 logistic regression， weighted logistic regression。

模型復雜度

我們已經介紹了訓練步驟，但是等等，還有一個重要的事情，那就是 regularization（正則化） ！ 我們需要定義樹的復雜度 Ω(f)Ω(f) 。為了做到這一點，讓我們首先改進一棵樹的定義 f(x)f(x) 如下

ft(x)=wq(x),w∈RT,q:Rd→{1,2,⋯,T}.ft(x)=wq(x),w∈RT,q:Rd→{1,2,⋯,T}.

這里 ww 是樹葉上的分數向量，qq 是將每個數據點分配給葉子的函數，TT 是樹葉的數量。 在 XGBoost 中，我們將復雜度定義為

Ω(f)=γT+12λ∑j=1Tw2jΩ(f)=γT+12λ∑j=1Twj2

當然有不止一種方法來定義復雜度，但是這個具體的方法在實踐中運行良好。正則化是大多數樹的包不那么謹慎或簡單忽略的一部分。這是因為對傳統的樹學習算法的對待只強調提高 impurity（不純性），而復雜度控制則是啟發式的。 通過正式定義，我們可以更好地了解我們正在學習什么，是的，它在實踐中運行良好。

The Structure Score（結構分數）

這是 derivation（派生）的神奇部分。在對樹模型進行重新格式化之后，我們可以用第 tt 棵樹來編寫目標值如 :

Obj(t)≈∑i=1n[giwq(xi)+12hiw2q(xi)]+γT+12λ∑j=1Tw2j=∑j=1T[(∑i∈Ijgi)wj+12(∑i∈Ijhi+λ)w2j]+γTObj(t)≈∑i=1n[giwq(xi)+12hiwq(xi)2]+γT+12λ∑j=1Twj2=∑j=1T[(∑i∈Ijgi)wj+12(∑i∈Ijhi+λ)wj2]+γT

其中 Ij={i|q(xi)=j}Ij={i|q(xi)=j} 是分配給第 jj 個葉子的數據點的索引的集合。 請注意，在第二行中，我們更改了總和的索引，因為同一葉上的所有數據點都得到了相同的分數。 我們可以通過定義 Gj=∑i∈IjgiGj=∑i∈Ijgi 和 Hj=∑i∈IjhiHj=∑i∈Ijhi 來進一步壓縮表達式 :

Obj(t)=∑j=1T[Gjwj+12(Hj+λ)w2j]+γTObj(t)=∑j=1T[Gjwj+12(Hj+λ)wj2]+γT

在這個等式中 wjwj 是相互獨立的，形式 Gjwj+12(Hj+λ)w2jGjwj+12(Hj+λ)wj2 是二次的，對於給定的結構 q(x)q(x) 的最好的 wjwj，我們可以得到最好的客觀規約:

w∗j=−GjHj+λObj∗=−12∑j=1TG2jHj+λ+γTwj∗=−GjHj+λObj∗=−12∑j=1TGj2Hj+λ+γT

最后一個方程度量一個樹結構 q(x)q(x) how good（到底有多好） 。

如果這一切聽起來有些復雜，我們來看一下圖片，看看分數是如何計算的。 基本上，對於一個給定的樹結構，我們把統計 gigi 和 hihi push 到它們所屬的葉子上，統計數據加和到一起，然后使用公式計算樹是多好。 除了考慮到模型的復雜度，這個分數就像決策樹中的雜質測量一樣（例如，熵/GINI系數）。

學習樹結構

既然我們有了一個方法來衡量一棵樹有多好，理想情況下我們會列舉所有可能的樹並挑選出最好的樹。 在實踐中，這種方法是比較棘手的，所以我們會盡量一次優化樹的一個層次。 具體來說，我們試圖將一片葉子分成兩片，並得到分數

Gain=12[G2LHL+λ+G2RHR+λ−(GL+GR)2HL+HR+λ]−γGain=12[GL2HL+λ+GR2HR+λ−(GL+GR)2HL+HR+λ]−γ

這個公式可以分解為 1) 新左葉上的得分 2) 新右葉上的得分 3) 原始葉子上的得分 4) additional leaf（附加葉子）上的正則化。 我們可以在這里看到一個重要的事實：如果增益小於 γγ，我們最好不要添加那個分支。這正是基於樹模型的 pruning（剪枝） 技術！通過使用監督學習的原則，我們自然會想出這些技術工作的原因 :)

對於真實有價值的數據，我們通常要尋找一個最佳的分割。為了有效地做到這一點，我們把所有的實例按照排序順序排列，如下圖所示。 

然后從左到右的掃描就足以計算所有可能的拆分解決方案的結構得分，我們可以有效地找到最佳的拆分。

XGBoost 最后的話

既然你明白了什么是 boosted trees 了，你可能會問這在 XGBoost 中的介紹在哪里？ XGBoost 恰好是本教程中引入的正式原則的動力！ 更重要的是，在 systems optimization（系統優化） 和 principles in machine learning（機器學習原理） 方面都有深入的研究。 這個庫的目標是推動機器計算極限的極端，以提供一個scalable（可擴展）, portable（可移植） 和 accurate（精確的） 庫。 確保你 試一試，最重要的是，向社區貢獻你的智慧（代碼，例子，教程）！