給定數據集 x(1),x(2),..,x(m),我們假使數據集是正常的,我們希望知道新的數據 xtest
是不 是異常的,即這個測試數據不屬於該組數據的幾率如何。我們所構建的模型應該能根據該測 試數據的位置告訴我們其屬於一組數據的可能性 p(x)。
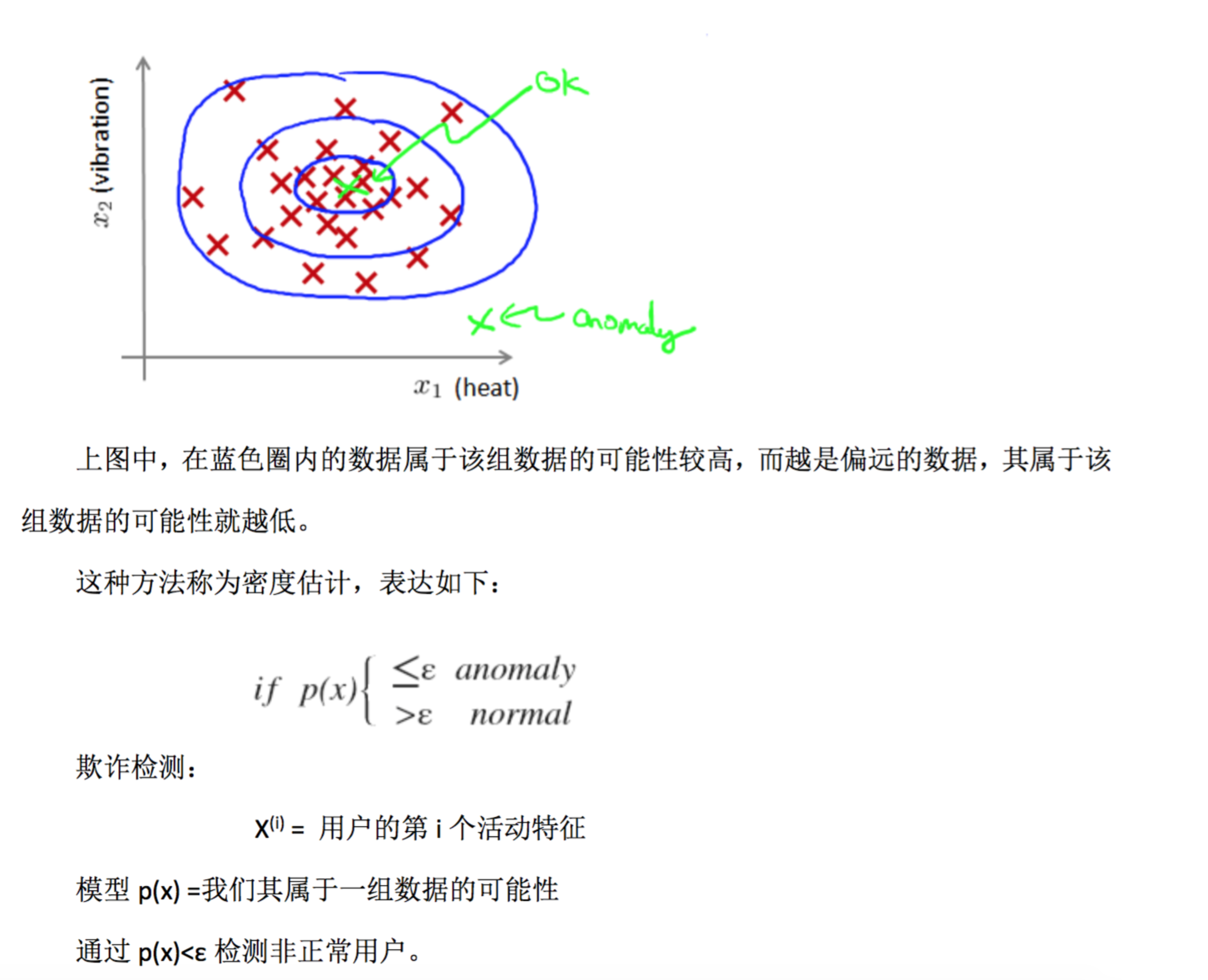
高斯分布 高斯分布,也稱為正態分布。回顧高斯分布的基本知識。 通常如果我們認為變量 x 符合高斯分布 x~N(μ,σ2)則其概率密度函數為:
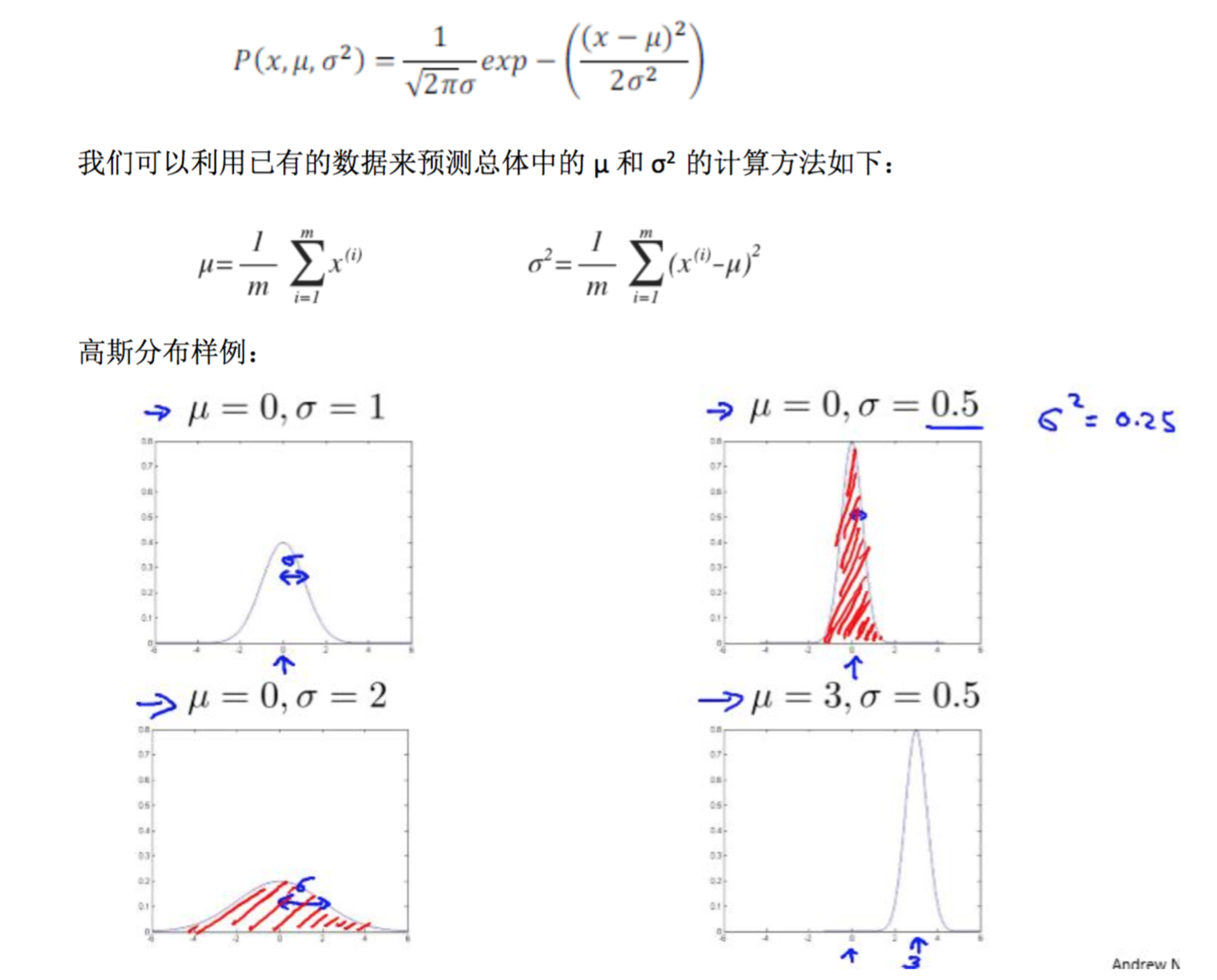
應用高斯分布開發異常檢測算法
異常檢測算法:
開發和評價一個異常檢測系統
異常檢測算法是一個非監督學習算法,意味着我們無法根據結果變量 y 的值來告訴我 們數據是否真的是異常的。我們需要另一種方法來幫助檢驗算法是否有效。當我們開發一個 異常檢測系統時,我們從帶標記(異常或正常)的數據着手,我們從其中選擇一部分正常數 據用於構建訓練集,然后用剩下的正常數據和異常數據混合的數據構成交叉檢驗集和測試 集。
例如:我們有 10000 台正常引擎的數據,有 20 台異常引擎的數據。 我們這樣分配數 據:
6000 台正常引擎的數據作為訓練集
2000 台正常引擎和 10 台異常引擎的數據作為交叉檢驗集 2000 台正常引擎和 10 台異常引擎的數據作為測試集 具體的評價方法如下:
- 根據測試集數據,我們估計特征的平均值和方差並構建 p(x)函數
- 對交叉檢驗集,我們嘗試使用不同的 ε 值作為閥值,並預測數據是否異常,根據 F1 值或者查准率與查全率的比例來選擇 ε
- 選出 ε 后,針對測試集進行預測,計算異常檢驗系統的 F1 值,或者查准率與查全 率之比
異常檢測與監督學習對比
之前我們構建的異常檢測系統也使用了帶標記的數據,與監督學習有些相似,下面的對 比有助於選擇采用監督學習還是異常檢測: 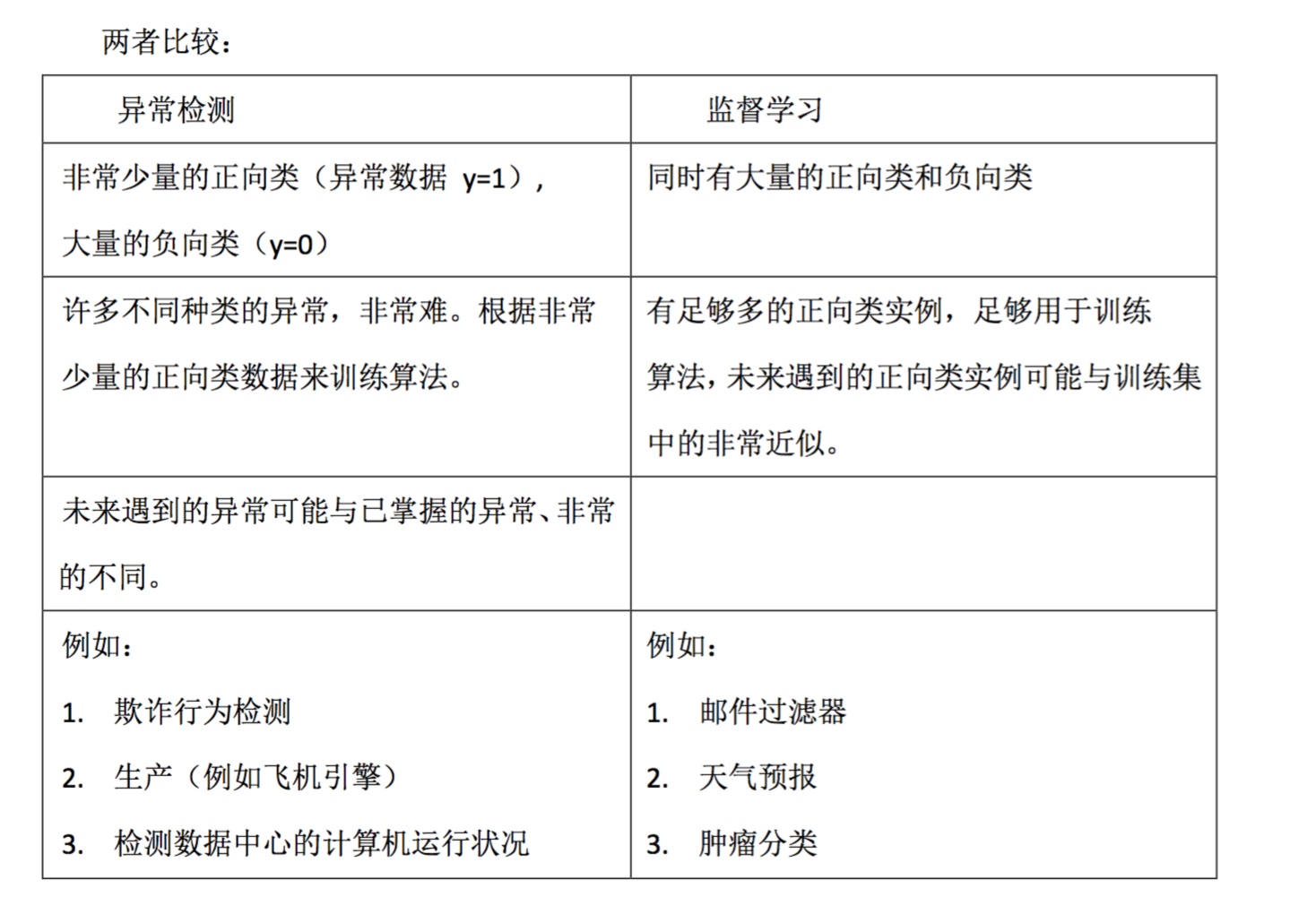
選擇特征
對於異常檢測算法,我們使用的特征是至關重要的,下面談談如何選擇特征:
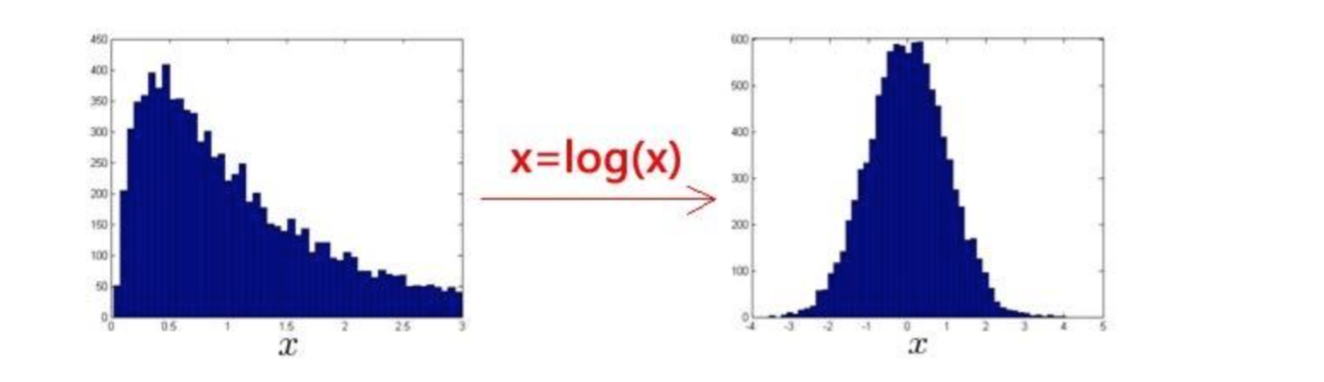
異常檢測假設特征符合高斯分布,如果數據的分布不是高斯分布,異常檢測算法也能夠 工作,但是最好還是將數據轉換成高斯分布,例如使用對數函數:x = log(x+c),其中 c 為非 負常數; 或者 x=xc
,c 為 0-1 之間的一個分數,等方法。
誤差分析:
一個常見的問題是一些異常的數據可能也會有較高的 p(x)值,因而被算法認為是正常的。 這種情況下誤差分析能夠幫助我們,我們可以分析那些被算法錯誤預測為正常的數據,觀察 能否找出一些問題。我們可能能從問題中發現我們需要增加一些新的特征,增加這些新特征 后獲得的新算法能夠幫助我們更好地進行異常檢測。
我們通常可以通過將一些相關的特征進行組合,來獲得一些新的更好的特征(異常數據 的該特征值異常地大或小),例如,在檢測數據中心的計算機狀況的例子中,我們可以用 CPU 負載與網絡通信量的比例作為一個新的特征,如果該值異常地大,便有可能意味着該服務器 是陷入了一些問題中。
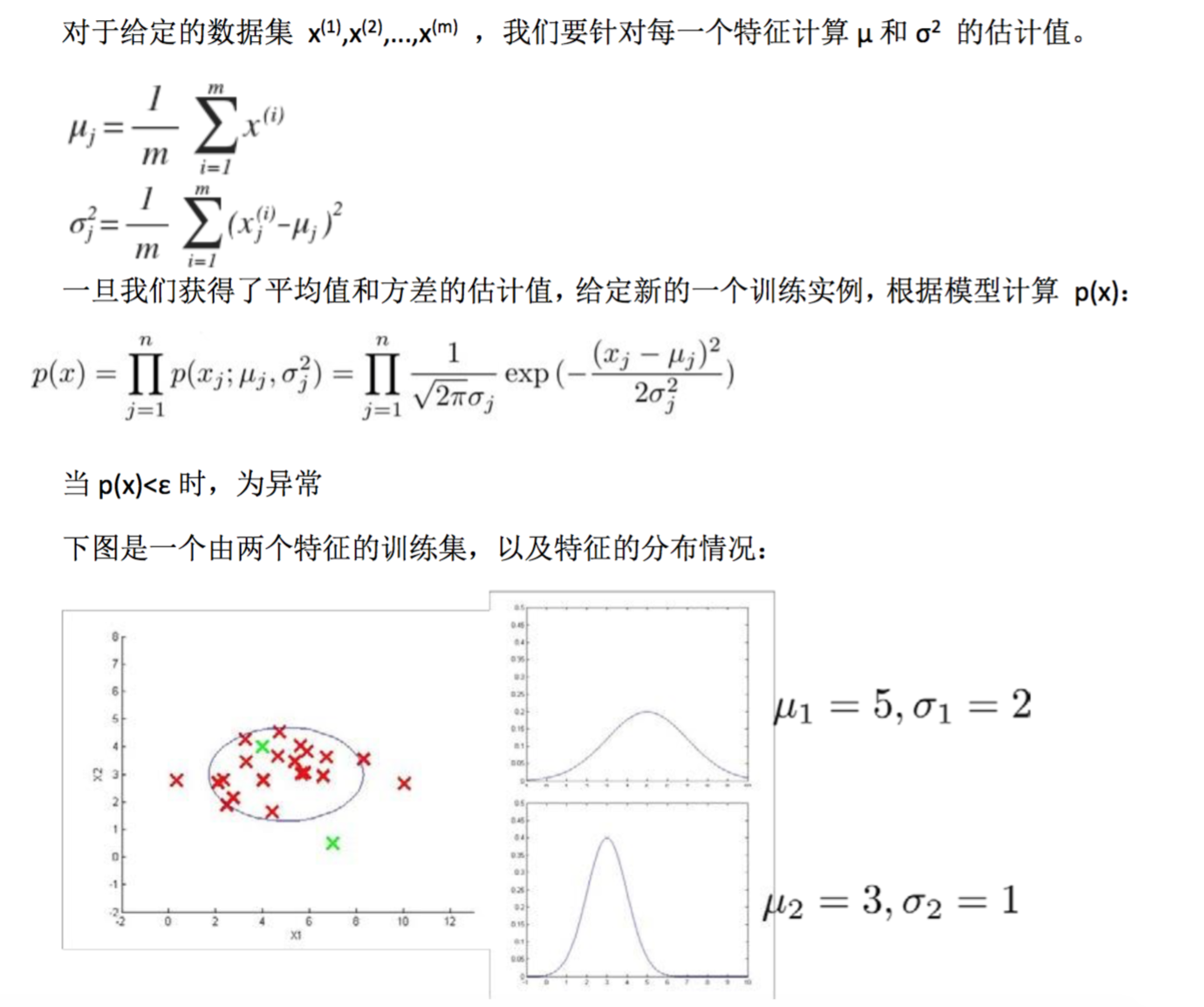
多元高斯分布
假使我們有兩個相關的特征,而且這兩個特征的值域范圍比較寬,這種情況下,一般的 高斯分布模型可能不能很好地識別異常數據。其原因在於,一般的高斯分布模型嘗試的是去 同時抓住兩個特征的偏差,因此創造出一個比較大的判定邊界。
下圖中是兩個相關特征,洋紅色的線(根據 ε 的不同其范圍可大可小)是一般的高斯分 布模型獲得的判定邊界,很明顯綠色的 X 所代表的數據點很可能是異常值,但是其 p(x)值卻 仍然在正常范圍內。多元高斯分布將創建像圖中藍色曲線所示的判定邊界。
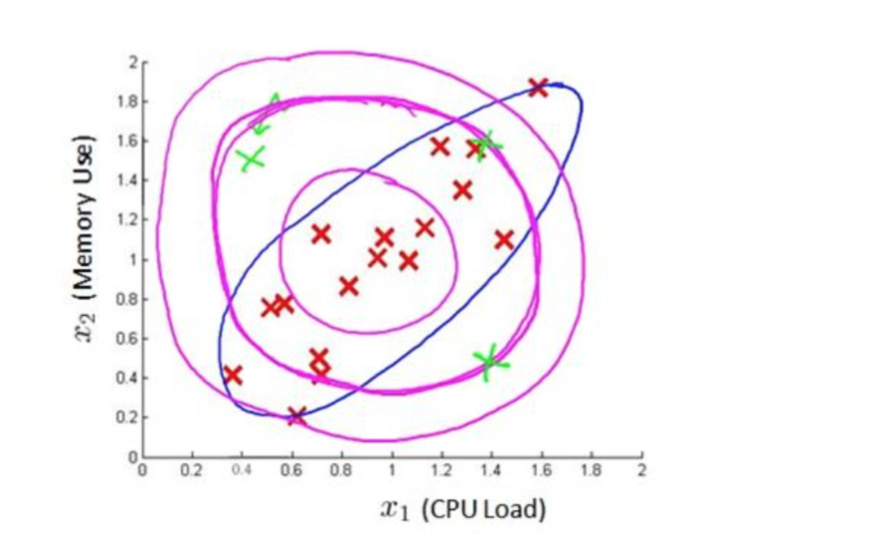
在一般的高斯分布模型中,我們計算 p(x)的方法是: 通過分別計算每個特征對應的幾 率然后將其累乘起來,在多元高斯分布模型中,我們將構建特征的協方差矩陣,用所有的特 征一起來計算 p(x)。

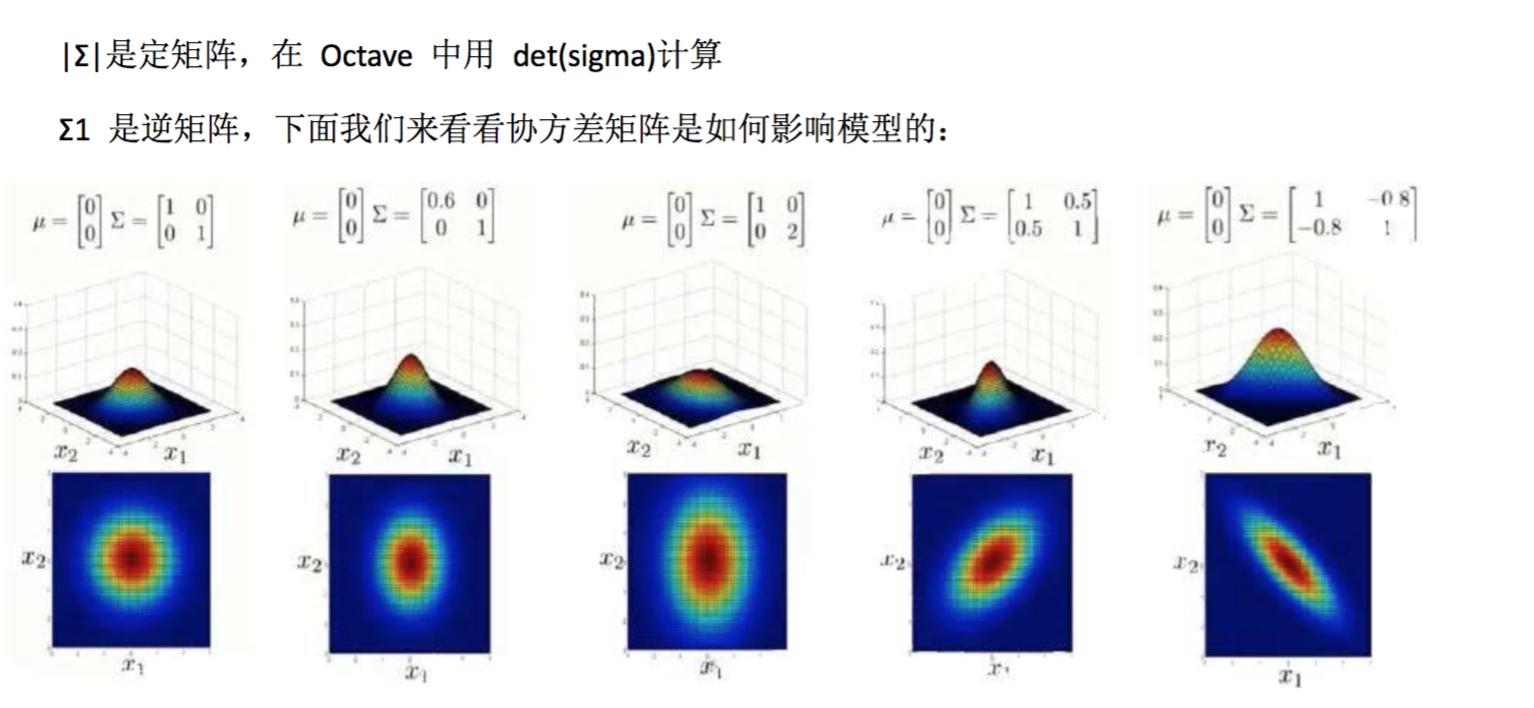
上圖是 5 個不同的模型,從左往右依次分析:
- 是一個一般的高斯分布模型
- 通過協方差矩陣,令特征 1 擁有較小的偏差,同時保持特征 2 的偏差
- 通過協方差矩陣,令特征 2 擁有較大的偏差,同時保持特征 1 的偏差
- 通過協方差矩陣,在不改變兩個特征的原有偏差的基礎上,增加兩者之間的正相關 性
- 通過協方差矩陣,在不改變兩個特征的原有偏差的基礎上,增加兩者之間的負相關 性
多元高斯分布模型與原高斯分布模型的關系: 可以證明的是,原本的高斯分布模型是多元高斯分布模型的一個子集,即像上圖中的第 1、2、3,3 個例子所示,如果協方差矩陣只在對角線的單位上有非零的值時,即為原本的 高斯分布模型了。
原高斯分布模型被廣泛使用着,如果特征之間在某種程度上存在相互關聯的情況,我們 可以通過構造新新特征的方法來捕捉這些相關性。 如果訓練集不是太大,並且沒有太多的特征,我們可以使用多元高斯分布模型。
摘自:http://whuhan2013.github.io/blog/2016/12/14/exception-and-recommd/
