1.神經網絡的起源
在傳統的編程方法中,我們通常會告訴計算機該做什么,並且將一個大問題分解為許多小的、精確的、計算機可以輕松執行的任務。相反,在神經網絡中,我們不告訴計算機如何解決問題,而是讓計算機從觀測數據中學習,自己找出解決方法。
自動從數據中學習聽起來不錯,然而,2006年之前我們都仍然不清楚如何訓練神經網絡使其優於大多數傳統方法,除了一些有專門解決方法的問題。在2006年,深度神經網絡出現了,這些技術現在被稱為深度學習,它們已經取得了進一步的發展。如今,深度神經網絡和深度學習在計算機視覺、語音識別及自然語言處理等重要領域都有卓越的性能表現,並且被谷歌、微軟和Facebook等公司大規模應用。
2.神經網絡的應用實例——識別手寫數字
考慮下列手寫數字。大多數人都能輕易地識別這些數字分別是:504192.
![]()
聽起來似乎很輕松,但實際上並不是這樣的。在我們人腦的兩個半球,有一個初級視覺皮層,也就是V1,包含了1.4億個神經元,它們之間的連接更是多達上百億個。然而,人類視覺系統不只是V1,而是包含了一整個系列的視覺皮層——V2,V3,V4,V5——以逐漸復雜地對圖像進行處理。
人類的大腦就像一台超級計算機,經過上億年的進化,從而更好地了解視覺世界。實際上,識別手寫數字並不容易,更准確地說,人類總是驚人地理解我們的眼睛所呈現給我們的信息。但幾乎所有工作都是無意識的,所以我們常常不清楚我們的視覺系統完成了多么困難的任務。
想要編寫程序來識別這些手寫數字是十分困難的,最直觀的經驗是“上邊有一個環路、右邊有一豎就是一個9了”,顯然用算法很難表達。當你想要得到這樣精確的規則描述時,你會很快迷失在特例和警告等特殊情況的困境中。這樣看起來似乎沒什么希望了。
而神經網絡卻能以一種不同的方式來解決這個問題。它的思想是:將大量手寫數字作為訓練實例,通過學習這些實例而獲得一個系統,這個系統就可以用來識別其它的手寫數字了。換句話說,神經網絡能利用這些實例自動地推斷出規則,從而識別手寫數字。如果增加訓練實例的數量,網絡可以學到更多的知識,從而提高識別的准確率。目前最好的商業神經網絡(識別手寫數字)用於銀行處理支票以及郵局識別信封上的地址。實現手寫數字識別的設計細節及代碼見此。

接下來介紹關於神經網絡的許多關鍵思想,包括兩種重要類型的人工神經元——感知器和sigmoid神經元,以及神經網絡的標准算法——隨機梯度下降法。
3.感知器
感知器在1957年由科學家Frank Rosenblatt提出,它可以被視為一種最簡單形式的前饋神經網絡,是一種二元線性分類器。
3.1 感知器是如何工作的
一個感知器需要多個二進制輸入x1,x2,……,並生成一個二進制輸出。下圖中的感知器有三個輸入x1,x2,x3,Rosenblatt提出一個簡單的規則來計算輸出。
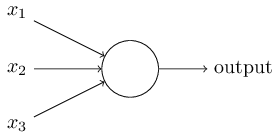
他引入了權值w1,w2,……,這些權值都是實數,分別表示各個輸入對輸出的重要性。感知器的輸出為0或1,取決於輸入的加權和∑wixi是否大於一個閾值。和權值一樣,閾值也是實數,是神經元的一個參數。用公式表示輸出如下圖:

這是一個基本的數學模型。你可以將感知器想象為一種設備,這個設備通過權衡各種證據(即輸入)做出決定(即輸出)。顯然,感知器不是人類決策系統的一個完整的模型,但一個復雜的感知器可以做出非常的決定:
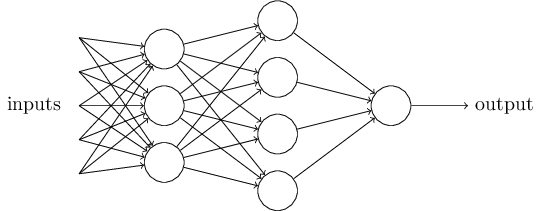
在這個網絡中,感知器的第一層通過權衡輸入而做出三個非常簡單的決定,第二層通過權衡第一層的輸出而做出四個稍微復雜的決定,第三層通過權衡第二層的輸出做出更復雜的決定,也就是感知器最終的輸出。這樣的話,多層感知器就可以做出復雜的決策。
為了簡化公式(1),我們使用w表示wi組成的向量,即權值向量;x表示xi組成的向量,即輸入向量;並將閾值移到不等式的左邊,然后用感知器的偏差b來代替閾值,感知器的公式就可以表示為:

可見,如果感知器的偏差b是一個很大的正值,該感知器很容易輸出1,相反,如果b是一個很大的負值,該感知器很難輸出1。引入偏差b這個概念變化看似很小,實際上使得公式得到了極大的簡化。我們不再需要閾值這個概念,而是偏差b。
3.2 感知器的應用
上面我們提到感知器可以權衡各項輸入做出決策,而它的另外一個應用就是做最基本的邏輯運算,也就是與、或、與非。舉個例子,假如我們有一個感知器,它需要兩個輸入,每個輸入的權值都是-2,偏差是3,如下圖左。當我們輸入00時,0*(-2)+0*(-2)+3=3,為正數,所以輸出為1;同樣的,輸入為01和10時,輸出都為1。而當輸入為11時,計算結果為-1,為負數,所以輸出為0。也就是說,當輸入為00、01、10時,輸出為1;輸入為11時,輸出為0。那么,這個感知器就實現了與非的功能。
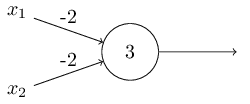
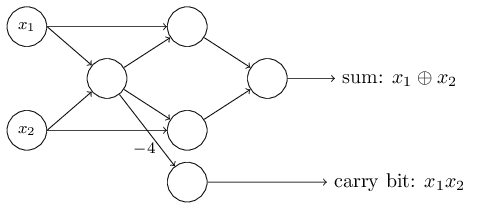
實際上,感知器可以實現任意邏輯運算。是因為與非是最基本的運算,我們可以在與非的基礎上實現其它邏輯運算,如上圖右。更多邏輯運算的例子見此。
就像與非是邏輯運算中的通用計算一樣(universal for computation),感知器也是神經網絡中的通用計算。感知器的計算通用性既讓人寬心又讓人沮喪:讓人寬心是因為它告訴我們,感知器網絡可以像任何其他計算設備一樣強大;讓人沮喪是因為它看起來就好像僅僅只是與非門的一種新類型。
但實際上的情況比這要好點。事實證明,我們可以設計學習算法來自動調整人工神經元網絡的權值和偏差。這個調整過程是對外部刺激的直接反應,而不需要程序員去干預,這一點是與傳統的邏輯門不同的。也就是說,我們的神經網絡是可以簡單地自己學會去解決問題的,這些問題不是直接設計一個傳統的邏輯回路能解決的。
4.sigmoid神經元
4.1 感知器的局限
學習算法,聽起來不錯。但是我們如何為一個神經網絡設計這樣的算法呢?假設現在我們有一個感知器網絡,我們想要讓其學會解決問題。舉個例子,網絡的輸入可能是一個手寫數字的掃描圖像的原始像素數據。現在我們希望這個網絡能學習到合適的權值和偏差,使得網絡的最終輸出能正確將這個數字分類。
為了看看這個學習過程是如何進行的,我們對網絡中一些權值(或偏差)做小小的改動。我們想要看到的是,對於權值的小小改動,將會導致網絡輸出有相應的改變。(我們稍后將會明白,這樣的屬性是使得學習過程成為可能的關鍵)大致意思如下圖所示:(當然,對於手寫數字識別的問題,下面這個網絡太簡單了)
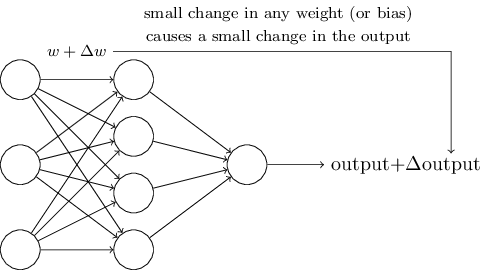
如果前面我們假設的“權值(或偏差)的改變能引起輸出的改變”是事實,那么我們就可以利用這一點去修改權值和偏差,使得我們的網絡按照我們的意願去工作。比如說,我們的網絡將“9”識別成了“8”,我們就可以想辦法改變權值和偏差,使得網絡更大可能地將圖像識別成“9”。然后我們就可以重復這一過程,不斷地改變權值和偏差,使得輸出越來越接近理想值。這樣看來,我們的網絡就具備了學習的能力。
問題是,當我們的網絡包含感知器時,並不會發生這樣的過程。事實上,在任何一個感知器中,對權值或偏差的小小改動可能會導致該感知器的輸出完全翻轉,也就是說從0變為了1。而這樣的翻轉可能會導致感知器接下來的識別工作發生徹底改變。所以說,就算你的“9”被識別正確了,對其它數字的識別可能會以難以控制的方式發生改變,比如將“6”識別成了“8”。
4.2 sigmoid神經元的出現
顯然,想要感知器具備學習能力是困難的。也許有更好的辦法,但這樣的可能似乎並不明顯。現如今,使用的是另一種更常見的人工神經元模型——sigmoid神經元,它可以克服這個問題。sigmoid神經元和感知器類似,但是它可以通過修改權值和偏差,使得輸出發生相應的變化。這使得sigmoid神經元網絡具備學習能力。
就像感知器一樣,sigmoid神經元也有輸入x1,x2,……,但不像感知器的輸入只能是0或1,sigmoid神經元的輸入可以是0到1之間的任意值,比如0.638。它也有權值w1,w2,……,以及整體偏差b。它的輸出也不再是0或1,而是σ(w*x+b),其中σ是sigmoid函數(sigmoid function),且其定義式如下右圖:


更明確地,一個sigmoid神經元的輸出如下圖式子所示。乍一看,sigmoid神經元好像與感知器完全不同。事實上,它們倆有許多相似之處。

為了更好地理解其中的相似之處,我們假設 z=w*x+b 是一個大的正數,所以 e^(-z)≈0,σ(z)≈1。也就是說,當 z=w*x+b 是一個很大的正數時,sigmoid神經元的輸出就很接近1,就像在感知器中一樣。相反,當 z=w*x+b 是一個絕對值很大的負數時,sigmoid神經元的輸出就很接近0,也類似於感知器。只有當 z=w*x+b 處於中間值時,sigmoid才與感知器不同。
4.3 sigmoid函數的形式
事實上,σ的確切形式並不重要,真正重要的是函數的形狀。上述提到的σ函數的形狀如下圖左。如下圖右是一個平滑的階躍函數。如果σ真的是一個階躍函數,那么sigmoid神經元就變成了一個感知器,因為輸出0或1就完全取決於 w*x+b 的正負了(實際上,當 w*x+b=0 時,感知器的輸出為0,而階躍函數的輸出為1。所以,嚴格來講,要想完全等於感知器,我們必須調整階躍函數在0點的值)。


可以發現,是σ函數的平滑度起了關鍵作用,而不是其具體形式。σ的平滑度意味着權值的變動Δwj或偏差的變動Δb將會對神經元的輸出所做的改變Δoutput,微積分可以給出Δoutput的近似值。下面這個公式告訴我們:Δoutput是Δwj和Δb的線性函數。所以sigmoid神經元能更容易地指出權值和偏差的改變是如何改變輸出的。

既然是σ函數的平滑度起了關鍵作用,而不是其具體形式,那么為什么用公式(3)中的形式呢?事實證明,當我們計算這些偏導數時,使用σ將簡化代數,僅僅因為指數很容易求微分。在任何情況下,σ在神經網絡中是被廣泛使用的,常作為激活函數。
4.4 sigmoid神經元的輸出
顯而易見,sigmoid神經元與感知器最大的不同就是輸出不再僅僅只是0或1,它可以輸出0-1之間的任意實數。這個屬性很有用,例如,如果我們想用輸出值表示一個輸入圖像中像素的平均強度。
但有時它又顯得很麻煩,假如我們想用網絡的輸出來表示“輸入圖像是9”和“輸入圖像不是9”中的一個。顯然,此時用感知器會更簡單。不過在實際應用中,我們可以設置一個規則來解決這個問題。例如,規定輸出大於或等於0.5時表示“輸入圖像是9”,輸出小於0.5時表示“輸入圖像不是9”(對圖片的像素強度進行編碼,如64*64個像素單元,就是64*64個輸入,輸出是一個介於0到1之間的值,最后比較其與0.5的大小)。
5.其它人工神經元模型
原則上,由sigmoid神經元組成的網絡可以計算任何函數。然而實際中,使用其它神經元模型組成的網絡有時性能會勝過sigmoid神經元的網絡,可能學習地更快,可能對測試數據更泛化,也可能兩者都有。下面我們就列舉幾個其它神經元模型。
5.1 tanh神經元
最簡單的變種——tanh神經元,用雙曲正切函數替代sigmoid函數。一個“輸入為x,權值向量為w,偏差為b”的tanh神經元的輸出如下圖所示。
tanh(x)=2f(2x)-1 。
它非常接近sigmoid神經元。我們知道tanh函數的公式如下式(110),可以推導出它和sigmoid函數的關系如式(111)所示。所以說,tanh函數相當於只是sigmoid函數的變種,並且可以在曲線圖中看出tanh函數和sigmoid函數有相同的形狀。

唯一的不同是:tanh神經元的輸出范圍為[-1,1],而sigmoid神經元的輸出為[0,1]。也就意味着,如果你在網絡中使用tanh神經元,你必須對你的結果進行歸一化(根據實際,也可能需要對輸入歸一化)。
和sigmoid神經元類似,tanh神經元也可以計算任何函數(compute any function),將輸入mapping到[-1,1]。此外,像BP和隨機梯度下降法也可以很容易地應用於tanh神經元的網絡中。
5.2 ReLu(自適應線性神經元)
sigmoid神經元的另一個變種就是自適應線性神經元ReLu(rectified linear neuron or rectified linear unit),一個“輸入為x,權值向量為w,偏差為b”的ReLu的輸出如下式(112)。用圖來表示自適應函數 max(0,z) 如下所示。
很明顯,這樣的神經元是與tanh神經元和sigmoid神經元都非常不同的。不過,ReLu神經元也是可以計算任何函數的,也可以用BP和隨機梯度下降法等思想來訓練。
那么,我們什么時候用ReLu而不是tanh神經元或sigmoid神經元呢?目前已經有許多在圖像識別上的工作發現了相當多使用ReLu的好處。
6.神經網絡的結構
神經網絡的結構如下圖,中間的隱藏層可以有多個。令人困惑的一點是,由於歷史原因,這樣的多層網絡有時又被稱為多層感知器或MLPs(multilayer perceptrons),盡管這些神經元是由sigmoid神經元組成的,而不是感知器。
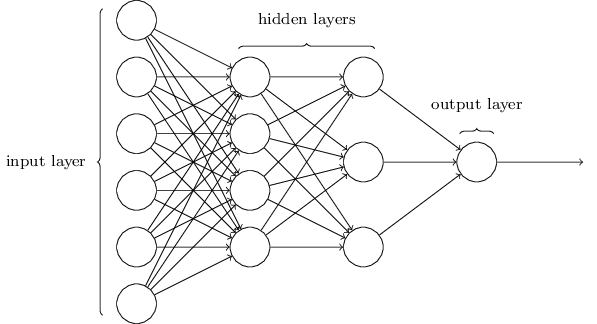
輸入層和輸出層的設計是顯而易見的,而隱藏層的設計則是一門藝術活,我們無法用幾個簡單的經驗法則就總結出隱藏層的設計過程。相反,神經網絡的研究人員們已經開發了許多設計隱藏層的啟發式方法,使得人們能得到他們滿意的網絡。這樣的啟發式方法能權衡隱藏層的數目和訓練網絡需要的時間兩者之間的力臂。
一層的輸出作為下一層的輸入,這樣的網絡稱為前饋神經網絡。這意味着網絡中不存在回環,信息總是向前傳播,並不會反饋。如果網絡中存在回環,我們將會陷入死循環:σ函數的輸入取決於輸出。這將會很難理解,所以我們不允許這樣的回環存在。
然而,還有其他允許反饋循環的人工神經網絡模型,這些神經網絡被稱為遞歸神經網絡。這些模型的思想是:存在一些只在有限時間內產生作用的神經元。這樣的神經元可以刺激其他神經元,其他神經元可能會在一段時間后產生作用,但也只能持續一段時間。接着再激活其他神經元,所以隨着時間推移,我們會得到神經元激活的一個級聯。在這樣的模型中,回環不會產生什么問題,因為一個神經元的輸出只會在一段時間后才對其自身的輸入產生作用,並不是瞬時的。
遞歸神經網絡(RNN)的影響不如前饋神經網絡,部分原因是RNN的學習算法並不是很強大(至少迄今為止是這樣)。但RNN仍然非常有趣,它們更接近人類大腦的運作方式。並且RNN很有可能能解決用前饋網絡很難解決的問題。
7.神經網絡向深度學習的發展
假如我們想確定一張圖像中是否有人臉,處理這個問題和識別手寫數字是一樣的方式。圖像中的像素作為神經網絡的輸入,網絡的輸出是單個神經元,並指示“Yes, it’s a face”或“No, it’s not a face”。
如果我們手動設計一個網絡會怎么樣?我們必須選擇合適的權值和偏差。這個時候,讓我們完全忘記神經網絡的概念,我們所能想到的啟發式方法就是我們可以將這個問題分解成子問題:圖像中是否有左眼?圖像中是否有右眼?圖像的中間是否有鼻子?圖像的中下部是否有嘴巴?圖像的頂部是否有頭發?等等問題。
如果像這類問題的多個都是“yes”,或者說“probably yes”,那我們就可以得出結論:這個圖像很有可能是一張人臉。如果像這類問題的多個都是“no”,那我們就可以得出結論:這個圖像很有可能不是一張人臉。
當然,這樣去判斷是很粗糙的,也有很多缺陷:也許這個人是一個禿子呢,所以他沒有頭發;也許我們看見的只是人臉的一部分,或者人臉不是正向朝向我們的,所以人臉的一部分特征被遮蔽了。
下面有一個也許可行的結構,其中一個矩形表示一個sub-network,也就是上面我們列舉的那些子問題。注意,這不是一個現實的方法來解決人臉識別的問題,它只是用來幫助我們直觀地感受網絡是如何工作的。
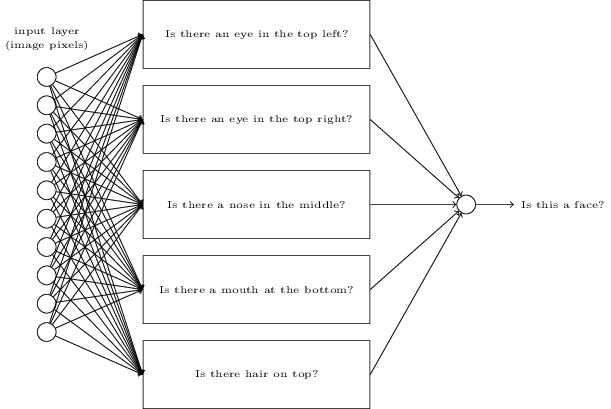
顯而易見,這些子問題也是可以再一次被分解的。比如,對於“是否有左眼”的問題,可以進一步分解為:“是否有眉毛”、“是否有睫毛”、“是否有虹膜”等等。當然,這些子子問題還包括位置信息,比如“眉毛是否在虹膜的上方”等,但這里讓我們盡可能地簡化。所以說,“是否有左眼”的問題可做如下分解:
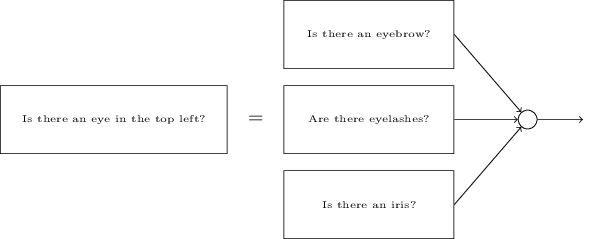
當然,其中的子子問題又可以進一步分解,通過分解多層來更進一步。直到最后,我們可以用像素這一層次來回答問題,比如“圖像中特定的位置是否出現簡單的形狀”這一類的問題。最后,網絡就將一個很復雜的問題分解成了非常簡單的問題。
這個網絡會有很多層,從具體到抽象,從復雜到簡單。這樣多層結構的網絡(具有兩層或更多隱藏層)就被稱為深度神經網絡(deep neural networks)。
我們當然沒法人工來選擇網絡的權值和偏差,我們還是必須使用學習算法使得網絡能自動地從訓練數據中學習到合適的權值和偏差。1980s和1990s,研究人員們嘗試使用隨機梯度下降法和反向傳播算法來訓練深度網絡,不幸的是,除了少數特殊結構,並沒有什么大的進展。網絡可以學習,但是很慢,因此沒什么用。
但自2006年以來,一系列的技術被發明,使得深度網絡的學習成為可能。雖然這些技術仍是基於隨機梯度下降法和反向傳播算法,但也有一些新的思想。這些技術使得更深(或更大)的網絡得到訓練——人們現在普遍訓練的網絡的隱藏層有5-10層。並且事實證明,在許多問題上,這些技術遠比淺層神經網絡(隱藏層只有一層的網絡)的性能更好。
這其中的原因肯定是深度網絡能建立更復雜的層次結構,這就像傳統編程語言使用模塊化的設計以及抽象的思想從而能創建復雜的計算機程序一樣。當然,在神經網絡和傳統編程中,抽象是不同的形式,但都是同等重要的。
參考文獻:
- Michael A.Nielsen, “Neural Networks and Deep Learning“, Determination Press, 2015.
- ReLu的好處:Kevin Jarrett, Koray Kavukcuoglu, Marc’Aurelio Ranzato and Yann LeCun, “What is the Best Multi-Stage Architecture for Object Recognition?” (2009)
- ReLu的好處:Xavier Glorot, Antoine Bordes, and Yoshua Bengio, “Deep Sparse Rectifier Neural Networks” (2011)
- ReLu的好處:Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton, “ImageNet Classification with Deep Convolutional Neural Networks” (2012)
- ReLu的好處:Vinod Nair and Geoffrey Hinton, “Rectified Linear Units Improve Restricted Boltzmann Machines” (2010)
- 安逸軒的博客:http://andyjin.applinzi.com/


