快速選擇算法,是一種能在大致O(N)的時間內選取數組中第k大或者k小的算法.其基本思路與快速排序算法類似,也是分治的思想.
其實這個算法是個基礎算法,但是不常用,所以今天編的時候錯了POJ2388,才有了這篇文章.
- 執行Partition算法(就是那個快排里將區間內所有數划分為小的一部分和大的一部分的過程)
- 判斷第k大的數是在小的部分還是大的部分
- 遞歸,直到區間足夠小,返回結果
下面幾段代碼,尤其要注意的是
while(i<j)
還是
while(i<=j)
程序1:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
/*
Program:快速選擇算法樣例
Author:Comzyh
*/
#include <cstdio>
int array[10000],temp;
int N,K;
int QuickSelect(int arr[],int b,int e,int k);
int main()
{
scanf("%d%d",N,K);
for (int i=1;i<=N;i++)
scanf("%d",array[i]);
printf("The k th :%d\n",QuickSelect(array,1,N,K));
}
int QuickSelect(int arr[],int b,int e,int k)
{
int i=b,j=e,mid=arr[(i+j)>>1];
while (i<=j)//注意,小於等於
{
while (arr[i]<mid)i++;
while (arr[j]>mid)j--;
if (i<=j)
{
temp=arr[i];arr[i]=arr[j];arr[j]=temp;
i++;j--;
}
}
if (b<j k<=j)return QuickSelect(arr,b,j,k);//分治
if (i<e k>=i)return QuickSelect(arr,i,e,k);
return arr[k];//如果不屬於任何一方,就結束,返回
}
|
不過,就是這樣一個簡單的算法,今天也出了點錯誤,本來我是用用了多少年的快排改的,就像下面這段代碼
程序2:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
/*
Program:快速排序算法樣例
Author:Comzyh
*/
#include <cstdio>
int array[10000],temp;
int N,K;
int QuickSort(int arr[],int b,int e);
int main()
{
scanf("%d",N);
for (int i=1;i<=N;i++)
scanf("%d",array[i]);
QuickSort(array,1,N);
for (int i=1;i<=N;i++)
printf("%d\n",array[i]);
}
int QuickSort(int arr[],int b,int e)
{
int i=b,j=e,mid=arr[(i+j)>>1];
while (i<j)//注意,小於
{
while (arr[i]<mid)i++;
while (arr[j]>mid)j--;
if (i<=j)
{
temp=arr[i];arr[i]=arr[j];arr[j]=temp;
i++;j--;
}
}
if (b<j)QuickSort(arr,b,j);
if (i<e)QuickSort(arr,i,e);
}
|
幾乎一模一樣,但是下面這樣寫就是是錯的
程序3:
|
1
2
3
4
5
6
7
8
9
10
11
|
int QuickSelect(int arr[],int b,int e,int k)
{
int i=b,j=e,mid=arr[(i+j)>>1];
while (i<j)//注意,小於
{
....
}
if (b<j k<=j)return QuickSelect(arr,b,j,k);//分治
if (i<e k>=i)return QuickSelect(arr,i,e,k);
return arr[k];//如果不屬於任何一方,就結束,返回
}
|
而這樣寫是對的
程序4:
|
1
2
3
4
5
6
7
8
9
10
11
|
int QuickSelect(int arr[],int b,int e,int k)
{
int i=b,j=e,mid=arr[(i+j)>>1];
while (i<j)//注意,小於
{
....
}
if (b<j k<=j)QuickSelect(arr,b,j,k);//沒有Return
if (i<e k>=i) QuickSelect(arr,i,e,k);
return arr[k];//如果不屬於任何一方,就結束,返回
}
|
快速排序已經模板化了,原理也清楚,實現也正確,但是,有些細節有可能理解不到位,所以才會出錯.
下面分析這種情況出現的原因:
出錯其實是一種極端情況,即向右掃描的指針i和向左掃描的指針j重合於k位置;.(這種巧合真的不大常見,但是還是讓我給碰上了,如果沒碰上,估計我的錯誤也不會被糾正.)
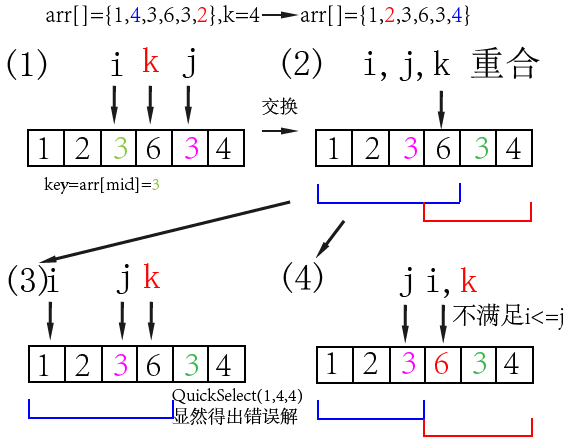
假設有一個數組arr[]={1,4,3,6,3,2},當k=4時;(
下標從1算起,下同)
首先,按照Partition算法,先交換arr[2]=4 和arr[6]=2,變成arr[]={1,2,3,6,3,4}
然后i=3,j=5
如圖(1)交換,i++,j–后,i=j=k=4
如圖(2)
- 按照錯誤的方法(程序3)執行(如圖(3)),函數會在閉區間[1,4]中尋找答案,這樣是錯誤的,因為arr[5]=3不在這個區間內
- 按照程序1中的方法執行,j會自減1,因為不滿足i<=j(i=4,j=3)然后會在閉區間[4,6]中遞歸(如圖(4)),尋找答案,這樣是正確的
- 按照程序4中的方法執行,QuickSelect(1,4,4)執行完之后arr[4]=6,這樣,再執行QuickSelect(4,6,4)時,程序會返回正確的結果