原文地址:http://www.cnblogs.com/rgvb178/p/6055213.html
版權聲明:本文為博主原創文章,未經博主允許不得轉載。
激活函數的作用
首先,激活函數不是真的要去激活什么。在神經網絡中,激活函數的作用是能夠給神經網絡加入一些非線性因素,使得神經網絡可以更好地解決較為復雜的問題。
比如在下面的這個問題中:

如上圖(圖片來源),在最簡單的情況下,數據是線性可分的,只需要一條直線就已經能夠對樣本進行很好地分類。

但如果情況變得復雜了一點呢?在上圖中(圖片來源),數據就變成了線性不可分的情況。在這種情況下,簡單的一條直線就已經不能夠對樣本進行很好地分類了。

於是我們嘗試引入非線性的因素,對樣本進行分類。
在神經網絡中也類似,我們需要引入一些非線性的因素,來更好地解決復雜的問題。而激活函數恰好能夠幫助我們引入非線性因素,它使得我們的神經網絡能夠更好地解決較為復雜的問題。
激活函數的定義及其相關概念
在ICML2016的一篇論文Noisy Activation Functions中,作者將激活函數定義為一個幾乎處處可微的 h : R → R 。

在實際應用中,我們還會涉及到以下的一些概念:
a.飽和
當一個激活函數h(x)滿足$$\lim_{n\to +\infty} h'(x)=0$$時我們稱之為右飽和。
當一個激活函數h(x)滿足$$\lim_{n\to -\infty} h'(x)=0$$時我們稱之為左飽和。當一個激活函數,既滿足左飽和又滿足又飽和時,我們稱之為飽和。
b.硬飽和與軟飽和
對任意的\(x\),如果存在常數\(c\),當\(x > c\)時恆有 \(h’(x) = 0\)則稱其為右硬飽和,當\(x < c\)時恆 有\(h’(x)=0\)則稱其為左硬飽和。若既滿足左硬飽和,又滿足右硬飽和,則稱這種激活函數為硬飽和。但如果只有在極限狀態下偏導數等於0的函數,稱之為軟飽和。
Sigmoid函數
Sigmoid函數曾被廣泛地應用,但由於其自身的一些缺陷,現在很少被使用了。Sigmoid函數被定義為:$$f(x)=\frac{1}{1+e^{-x}}$$函數對應的圖像是:

優點:
1.Sigmoid函數的輸出映射在\((0,1)\)之間,單調連續,輸出范圍有限,優化穩定,可以用作輸出層。
2.求導容易。
缺點:
1.由於其軟飽和性,容易產生梯度消失,導致訓練出現問題。
2.其輸出並不是以0為中心的。
##tanh函數 現在,比起Sigmoid函數我們通常更傾向於tanh函數。tanh函數被定義為$$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$ 函數位於[-1, 1]區間上,對應的圖像是: 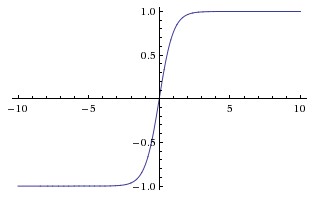 **優點:** 1.比Sigmoid函數收斂速度更快。 2.相比Sigmoid函數,其輸出以0為中心。 **缺點:** 還是沒有改變Sigmoid函數的最大問題——由於飽和性產生的梯度消失。
##ReLU ReLU是最近幾年非常受歡迎的激活函數。被定義為$$y= \begin{cases} 0& (x\le0)\\ x& (x>0) \end{cases}$$對應的圖像是: 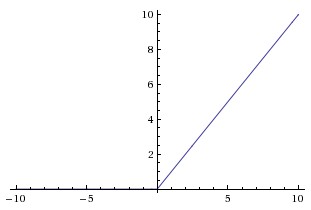 但是除了ReLU本身的之外,TensorFlow還提供了一些相關的函數,比如定義為min(max(features, 0), 6)的tf.nn.relu6(features, name=None);或是CReLU,即tf.nn.crelu(features, name=None)。其中(CReLU部分可以參考[這篇論文][4])。 **優點:** 1.相比起Sigmoid和tanh,ReLU[(e.g. a factor of 6 in Krizhevsky et al.)][5]在SGD中能夠快速收斂。例如在下圖的實驗中,在一個四層的卷積神經網絡中,實線代表了ReLU,虛線代表了tanh,ReLU比起tanh更快地到達了錯誤率0.25處。據稱,這是因為它線性、非飽和的形式。 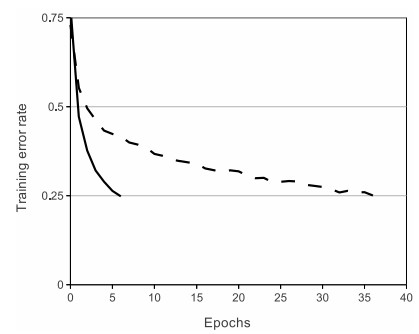 2.Sigmoid和tanh涉及了很多很expensive的操作(比如指數),ReLU可以更加簡單的實現。 3.有效緩解了梯度消失的問題。 4.在沒有無監督預訓練的時候也能有較好的表現。 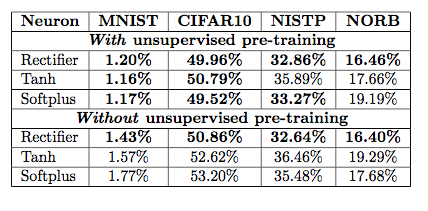 5.提供了神經網絡的稀疏表達能力。
缺點:
隨着訓練的進行,可能會出現神經元死亡,權重無法更新的情況。如果發生這種情況,那么流經神經元的梯度從這一點開始將永遠是0。也就是說,ReLU神經元在訓練中不可逆地死亡了。
##LReLU、PReLU與RReLU 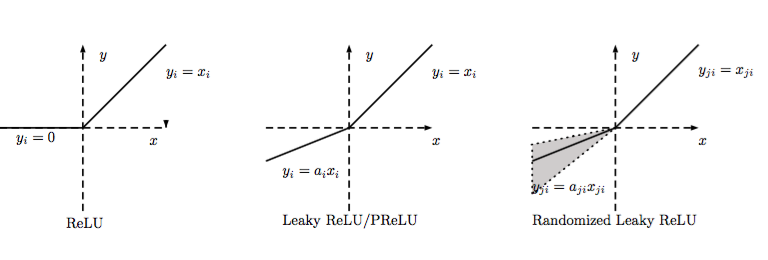
通常在LReLU和PReLU中,我們定義一個激活函數為
-LReLU
當\(a_i\)比較小而且固定的時候,我們稱之為LReLU。LReLU最初的目的是為了避免梯度消失。但在一些實驗中,我們發現LReLU對准確率並沒有太大的影響。很多時候,當我們想要應用LReLU時,我們必須要非常小心謹慎地重復訓練,選取出合適的\(a\),LReLU的表現出的結果才比ReLU好。因此有人提出了一種自適應地從數據中學習參數的PReLU。
-PReLU
PReLU是LReLU的改進,可以自適應地從數據中學習參數。PReLU具有收斂速度快、錯誤率低的特點。PReLU可以用於反向傳播的訓練,可以與其他層同時優化。

在論文Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification中,作者就對比了PReLU和ReLU在ImageNet model A的訓練效果。
值得一提的是,在tflearn中有現成的LReLU和PReLU可以直接用。
-RReLU
在RReLU中,我們有$$y_{ji}=\begin{cases}
x_{ji}& if(x_{ji}>0)\
a_{ji}x_{ji}& if(x_{ji}\le0)
\end{cases}$$$$a_{ji} \sim U(l,u),l<u;;and;;l,u\in [0,1) $$
其中,\(a_{ji}\)是一個保持在給定范圍內取樣的隨機變量,在測試中是固定的。RReLU在一定程度上能起到正則效果。

在論文Empirical Evaluation of Rectified Activations in Convolution Network中,作者對比了RReLU、LReLU、PReLU、ReLU 在CIFAR-10、CIFAR-100、NDSB網絡中的效果。
ELU
ELU被定義為$$f(x)=\begin{cases}
a(e^x-1)& if(x<0)\
x& if(0\le x)
\end{cases}$$其中\(a>0\)。

優點:
1.ELU減少了正常梯度與單位自然梯度之間的差距,從而加快了學習。
2.在負的限制條件下能夠更有魯棒性。
ELU相關部分可以參考這篇論文。
Softplus與Softsign
Softplus被定義為$$f(x)=log(e^x+1)$$
Softsign被定義為$$f(x)=\frac{x}{|x|+1}$$
目前使用的比較少,在這里就不詳細討論了。TensorFlow里也有現成的可供使用。激活函數相關TensorFlow的官方文檔
##總結 關於激活函數的選取,目前還不存在定論,實踐過程中更多還是需要結合實際情況,考慮不同激活函數的優缺點綜合使用。同時,也期待越來越多的新想法,改進目前存在的不足。
文章部分圖片或內容參考自:
CS231n Convolutional Neural Networks for Visual Recognition
Quora - What is the role of the activation function in a neural network?
深度學習中的激活函數導引
Noisy Activation Functions-ICML2016
本文為作者的個人學習筆記,轉載請先聲明。如有疏漏,歡迎指出,不勝感謝。
