[LeetCode] 208. Implement Trie (Prefix Tree) 實現字典樹(前綴樹)

 

Implement a trie with insert, search, and startsWith methods.

Example:

Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // returns true
trie.search("app");     // returns false
trie.startsWith("app"); // returns true
trie.insert("app");   
trie.search("app");     // returns true

Note:

• You may assume that all inputs are consist of lowercase letters a-z.
• All inputs are guaranteed to be non-empty strings.

 

這道題讓我們實現一個重要但又有些復雜的數據結構-字典樹， 又稱前綴樹或單詞查找樹，詳細介紹可以參見網友董的博客，例如，一個保存了8個鍵的trie結構，"A", "to", "tea", "ted", "ten", "i", "in", and "inn"，如下圖所示：

 

 

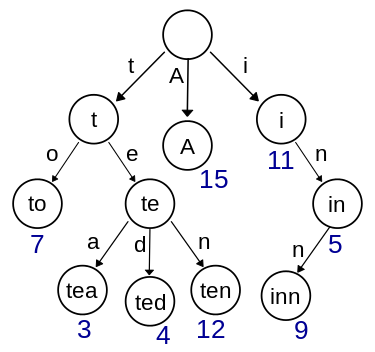
字典樹主要有如下三點性質：

1. 根節點不包含字符，除根節點意外每個節點只包含一個字符。

2. 從根節點到某一個節點，路徑上經過的字符連接起來，為該節點對應的字符串。

3. 每個節點的所有子節點包含的字符串不相同。

 

字母樹的插入（Insert）、刪除（ Delete）和查找（Find）都非常簡單，用一個一重循環即可，即第i 次循環找到前i 個字母所對應的子樹，然后進行相應的操作。實現這棵字母樹，我們用最常見的數組保存（靜態開辟內存）即可，當然也可以開動態的指針類型（動態開辟內存）。至於結點對兒子的指向，一般有三種方法：

1、對每個結點開一個字母集大小的數組，對應的下標是兒子所表示的字母，內容則是這個兒子對應在大數組上的位置，即標號；

2、對每個結點掛一個鏈表，按一定順序記錄每個兒子是誰；

3、使用左兒子右兄弟表示法記錄這棵樹。

三種方法，各有特點。第一種易實現，但實際的空間要求較大；第二種，較易實現，空間要求相對較小，但比較費時；第三種，空間要求最小，但相對費時且不易寫。 

我們這里只來實現第一種方法，這種方法實現起來簡單直觀，字母的字典樹每個節點要定義一個大小為 26 的子節點指針數組，然后用一個標志符用來記錄到當前位置為止是否為一個詞，初始化的時候講 26 個子節點都賦為空。那么 insert 操作只需要對於要插入的字符串的每一個字符算出其的位置，然后找是否存在這個子節點，若不存在則新建一個，然后再查找下一個。查找詞和找前綴操作跟 insert 操作都很類似，不同點在於若不存在子節點，則返回 false。查找次最后還要看標識位，而找前綴直接返回 true 即可。代碼如下：

 

class TrieNode {
public:
    TrieNode *child[26];
    bool isWord;
    TrieNode(): isWord(false) {
        for (auto &a : child) a = nullptr;
    }
};

class Trie {
public:
    Trie() {
        root = new TrieNode();
    }
    void insert(string s) {
        TrieNode *p = root;
        for (auto &a : s) {
            int i = a - 'a';
            if (!p->child[i]) p->child[i] = new TrieNode();
            p = p->child[i];
        }
        p->isWord = true;
    }
    bool search(string key) {
        TrieNode *p = root;
        for (auto &a : key) {
            int i = a - 'a';
            if (!p->child[i]) return false;
            p = p->child[i];
        }
        return p->isWord;
    }
    bool startsWith(string prefix) {
        TrieNode *p = root;
        for (auto &a : prefix) {
            int i = a - 'a';
            if (!p->child[i]) return false;
            p = p->child[i];
        }
        return true;
    }
    
private:
    TrieNode* root;
};

 

Github 同步地址： 

https://github.com/grandyang/leetcode/issues/208

 

類似題目：

Add and Search Word - Data structure design

Design Search Autocomplete System

Replace Words

Implement Magic Dictionary

 

參考資料：

https://leetcode.com/problems/implement-trie-prefix-tree/

https://leetcode.com/problems/implement-trie-prefix-tree/discuss/58832/AC-JAVA-solution-simple-using-single-array

https://leetcode.com/problems/implement-trie-prefix-tree/discuss/58986/Concise-O(1)-JAVA-solution-based-on-HashMap

https://leetcode.com/problems/implement-trie-prefix-tree/discuss/58842/Maybe-the-code-is-not-too-much-by-using-%22next26%22-C%2B%2B

 

LeetCode All in One 題目講解匯總(持續更新中...)