概念
在了解二進制編碼之前,我們首先需要建立一個完整的體系架構
- 熵編碼
即編碼過程中按熵原理不丟失任何信息的編碼。信息熵為信源的平均信息量(不確定性的度量)。常見的熵編碼有:香農(Shannon)編碼、哈夫曼(Huffman)編碼和算術編碼(arithmetic coding)。 - CABAC
CABAC(Context-based Adaptive Binary Arithmetic Coding),基於上下文的自適應二進制算術編碼。CABAC是H.264/AVC標准中兩種熵編碼中的一種,它的編碼核心算法就是算術編碼(Arithmetic Coding)

熵編碼
VLC 編碼:
讓我們假設我們有一個符號流:a, e, r 和 t,它們的概率(從0到1)由下表所示。
| a | e | r | t | |
|---|---|---|---|---|
| 概率 | 0.3 | 0.3 | 0.2 | 0.2 |
我們可以分配不同的二進制碼,(最好是)小的碼給最可能(出現的字符),大些的碼給最少可能(出現的字符)。
| a | e | r | t | |
|---|---|---|---|---|
| 概率 | 0.3 | 0.3 | 0.2 | 0.2 |
| 二進制碼 | 0 | 10 | 110 | 1110 |
讓我們壓縮 eat 流,假設我們為每個字符花費 8 bit,在沒有做任何壓縮時我們將花費 24 bit。但是在這種情況下,我們使用各自的代碼來替換每個字符,我們就能節省空間。
第一步是編碼字符 e 為 10,第二個字符是 a,追加(不是數學加法)后是 [10][0],最后是第三個字符 t,最終組成已壓縮的比特流 [10][0][1110] 或 1001110,這只需 7 bit(比原來的空間少 3.4 倍)。
請注意每個代碼必須是唯一的前綴碼,Huffman 能幫你找到這些數字。雖然它有一些問題,但是視頻編解碼器仍然提供該方法,它也是很多應用程序的壓縮算法。
編碼器和解碼器都必須知道這個(包含編碼的)字符表,因此,你也需要傳送這個表。
算術編碼
讓我們假設我們有一個符號流:a, e, r, s 和 t,它們的概率由下表所示。
| a | e | r | s | t | |
|---|---|---|---|---|---|
| 概率 | 0.3 | 0.3 | 0.15 | 0.05 | 0.2 |
考慮到這個表,我們可以構建一個區間,區間包含了所有可能的字符,字符按出現概率排序。

讓我們編碼 eat 流,我們選擇第一個字符 e 位於 0.3 到 0.6 (但不包括 0.6)的子區間,我們選擇這個子區間,按照之前同等的比例再次分割。

讓我們繼續編碼我們的流 eat,現在使第二個 a 字符位於 0.3 到 0.39 的區間里,接着再次用同樣的方法編碼最后的字符 t,得到最后的子區間 0.354 到 0.372。
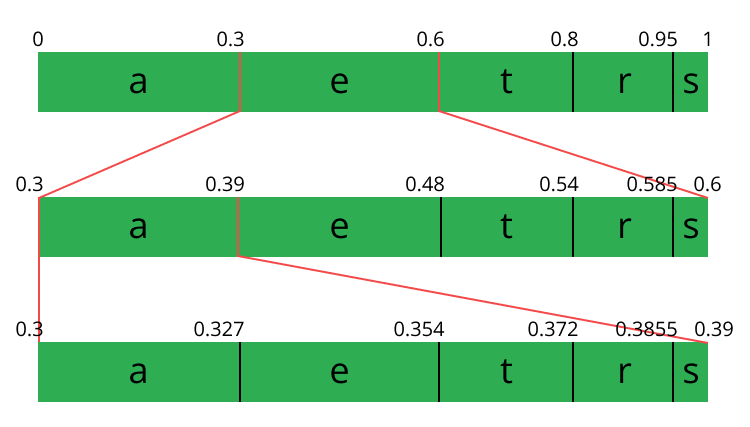
我們只需從最后的子區間 0.354 到 0.372 里選擇一個數,讓我們選擇 0.36,不過我們可以選擇這個子區間里的任何數。僅靠這個數,我們將可以恢復原始流 eat。就像我們在區間的區間里畫了一根線來編碼我們的流。
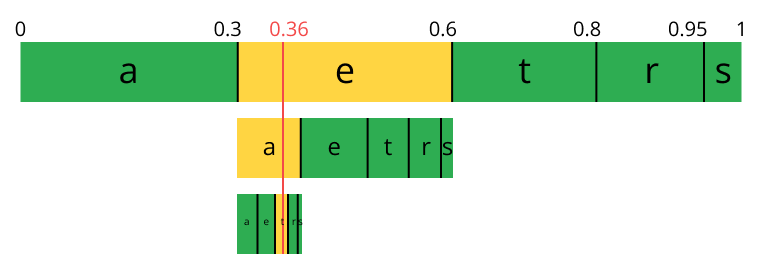
反向過程(又名解碼)一樣簡單,用數字 0.36 和我們原始區間,我們可以進行同樣的操作,不過現在是使用這個數字來還原被編碼的流。
在第一個區間,我們發現數字落入了一個子區間,因此,這個子區間是我們的第一個字符,現在我們再次切分這個子區間,像之前一樣做同樣的過程。我們會注意到 0.36 落入了 a 的區間,然后我們重復這一過程直到得到最后一個字符 t(形成我們原始編碼過的流 eat)。
編碼器和解碼器都必須知道字符概率表,因此,你也需要傳送這個表。
二進制算術編碼
二進制算術編碼的編碼方法跟算術編碼是一樣的,但是輸入只有兩個符號:“0”,“1”,也就是說輸入的是二進制串。
除了是對二進制串進行編碼這個特征外,二進制算術編碼跟普通的算術編碼還有一些區別,總體上可以按照如下進行描述:
設輸入符號串為s,s中的符號分為兩種:MPS(Most Probability Symbol),LPS(Low Probality Symbol),分別代表出現概率大小的符號,需要根據實際情況進行調整。如果輸入的二進制串中的“0”較多,“1”較少,那么MPS = “0”,LPS =“1”
在編碼中進行區間選擇時,MPS在前,LPS在后

與算術編碼的方式相同,我們最終可以通過這個數字還原出編碼的二進制串
CABAC
CABAC(Context-based Adaptive Binary Arithmetic Coding),基於上下文的自適應二進制算術編碼
問題1:如何建立起一個01字符概率表
問題2:什么叫上下文
問題3:什么叫自適應
通過分片,對每一片(slice)進行動態的更新符號概率表
問題4:如何將待編碼內容變成01串
參考文章
數字視頻編碼基礎(https://github.com/leandromoreira/digital_video_introduction)
CABAC編碼解析(https://blog.csdn.net/novice_growth/article/details/70830835)
