【前言】
在補Codeforce的DP時遇到一個比較新穎的題,然后在知乎上剛好 hycc 桑也寫了這道題的相關題解,這里是作為學習並引用博客的部分內容
這道題追根溯源發現2016年這個算法已經在APIO2016煙花表演與Codeforces 713C引入,自那之后似乎便銷聲匿跡了。相關題型數量也較少,因而在這里結合前輩們的工作做一些總結。---by hycc
問題引入:Codeforces 713C
題目鏈接:Here
題意:
-
給定 \(n\) 個正整數 \(a_i\) ,每次操作可以選擇任意一個數將其 \(+1\) 或 \(-1\) ,問至少需要多少次操作可以使得 \(n\) 個數保持嚴格單增。
-
數據范圍:\(1\le n\le 3000,1\le a_i\le 10^9\)
對我來說這道題其實和曾經寫過的 POJ-3666:求不升的DP是一樣的
這個題是求升序的DP,那么有什么變化呢
不升的條件是:\(a_i -a_j \ge 0\)
升序的條件是:\(a_i -a_j \ge i - j\) 對任意 \(i,j\) 均滿足
有沒有理解到什么?移項有:\(a_i - i \ge a_j - j\)
所以將 \(a\) 數字變形一下就和POJ3666就是一個題!
【AC Code】
const int N = 3100;
int n, m;
ll f[N][N], a[N], b[N];
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
a[i] = a[i] - i;
b[i] = a[i];
}
sort(b + 1, b + 1 + n);
m = 1;
for (int i = 2; i <= n; ++i) if (b[i] != b[i - 1]) b[++m] = b[i];
memset(f, 0, sizeof(f));
for (int i = 1; i <= n; ++i) {
ll Min = LLONG_MAX;
for (int j = 1; j <= m; j++) {
Min = min(Min, f[i - 1][j]);
f[i][j] = abs(b[j] - a[i]) + Min;
}
}
ll ans = LLONG_MAX;
for (int i = 1; i <= m; ++i) ans = min(ans, f[n][i]);
cout << ans << "\n";
}
當然上面說的思路並不是本篇博客實際想表達,以下才是正文
對於朴素的 \(\mathcal{O}(n^2)\ DP\) :
一個顯然的性質:如果不是“嚴格單增”而是“嚴格非降”,那么最終形成的嚴格非降序列,其中每個元素一定屬於 \(\{a_i\}\)
將元素離散化后可以設計 \(f_{i,j}\) 表示到第 \(i\) 個數取 \(j\) 的最少操作數
那么有轉移 \(f_{i,j} = \min\limits_{k\le j}f_{i-1,k} + | a_i - j|\) ,記錄 \(f_{i-1,*}\) 的前綴 \(\min\) 即可做到 \(\mathcal{O}(n^2)\)
至於如何做到“嚴格非降”,\(a_{i-1} < a_i,a_{i -1} \le a_i - i,a_{i-1}-(i-1)\le a_i - i\)
於是令 \(a_i = a_i - i\) 即可。
賽后的評論區中出現了一種 \(\mathcal{O}(Nlog\ N)\) 的做法,也就是 Slope Trick算法的第一次現身(?)
Slope Trick:解決一類凸代價函數的DP優化問題
當序列DP的轉移代價函數為
連續
分段線性函數
凸函數
時,可以通過記錄分段函數的最右一段 \(f_r(x)\) 以及其分段點 \(L\) 實現快速維護代價的效果。
如:\(f(x)=\left\{\begin{array}{rr} -x-3 & (x \leq-1) \\ x & (-1<x \leq 1) \\ 2 x-1 & (x>1) \end{array}\right.\)
可以僅記錄 \(f_r(x) = 2x - 3\) 與分段點 \(L_f = \{-1,-1,1\}\) 來實現對該分段函數的存儲。
注意:要求相鄰分段點之間函數的斜率差為 \(1\) ,也就是說相鄰兩段之間斜率差 \(\ge 1\) 的話,這個分段點要在序列里出現多次。
優秀的性質:
\(F(x),G(x)\) 均為滿足上述條件的分段線性函數,那么 \(H(x) =F(x)+G(x)\) 同樣為滿足條件的分段線性函數,且 \(H_r(x) = F_r(x) + G_r(x),L_H = L_F \bigcup L_G\) 。
該性質使得我們可以很方便得運用數據結構維護 \(L\) 序列。
回顧:Codeforces 713C
轉移方程為 \(f_{i,j} = \min\limits_{k\le j}f_{i-1,k} + |a_i - j|\)
令 \(F_{i}(x)=f_{i, x}, G_{i}(x)=\min\limits _{k \leq x} f_{i-1, k}=\min \limits_{k \leq x} F_{i-1}(k)\)
那么有 \(F_i(x) = G_i(x) + |x -a_i|\) ,其中 \(F_i,G_i\) 均為分段線性函數。
\(G_i\) 求的是 \(F_{i-1}\) 的關於函數值的前綴最小值,由於 \(F_{i-1}\) 是一個凸函數,因而其最小值應該在斜率 \(=0\) 處取得,其后部分可以舍去。
而每次由 \(G_i(x)\) 加上 \(|x-a_i|\) ,等價於在 \(L\) 中添加兩個分段點 \(\{a_i,a_j\}\)
因而 \(G_i\) 各段的函數斜率形如 \(\{...,-3,-2,-1,0\}\) ,加上 $|x-a_i| $后斜率變為 \(\{...,-3,-2,-1,0,1\}\) ,因而需要刪除末尾的分段點。
具體實現中:使用大根堆維護分段點單調有序,每次加入兩個 \(a_i\) ,再彈出堆頂元素。
總復雜度 :\(\mathcal{O}(n\ log\ n)\)
Codeforces 1534G
題意:
一個無限大的二維平面上存在 \(n\) 個點 \((x_i,y_i)\) 均需要被訪問一次,從 \((0,0)\) 出發,每次可以向右或向上移動一個單位。
可以在任意位置 \((X,Y)\) 訪問 \((x_i,y_i)\) 並付出 \(\max\{|X-x_i|,|Y-y_i|\}\) 的代價(訪問后依然留在 \((X,Y)\) )。同一位置可以訪問多個點。
問:至少需要花費多少代價才能使得所有點均被訪問?
數據范圍: \(1\le n\le 800000,0\le x_i,y_i\le 10^9\)
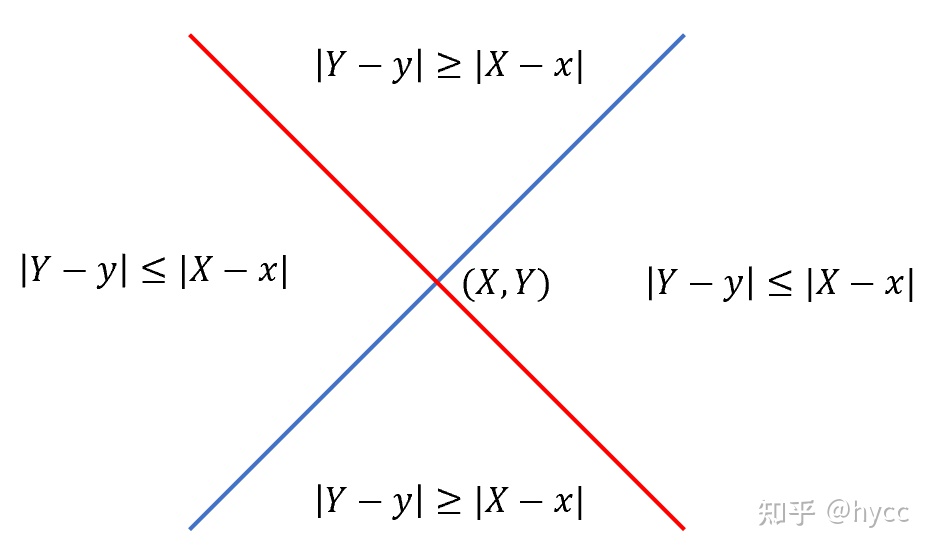
結合上圖可以看出,對於點 \((X,Y)\) ,一定會選擇路徑與直線 \(x+y=X+Y\)(紅線)的交點 \((x,y)\) 處作為訪問的發起點(在這條線上 \(|X-x| = |Y-y|\) )。
考慮到這條紅線是傾斜的,因而將坐標系順時針翻轉 \(45^°\),即 \((x+y,x-y)\) 代替 \((x,y)\)
此時,每次移動變為 \((x+1,y-1)\) 或 \((x+1,y+1)\)
把所有點按新的 \(x\) 坐標排序,即可轉為序列上的問題。
設值域為 \(M\) ,則很容易寫出 \(\mathcal{O}(nM)\) 的轉移方程:
\(f_{i,Y}\) 表示從左到右考慮到橫坐標為 \(x_i\) 的所有點,當前路徑到了 \((x_i,Y)\) 的最小代價,
那么有
$f_{i,Y}=\min\limits_{Y-\left|x_{i}-x_{i-1}\right|\leq k\leq Y+\left|x_{i}-x_{i-1}\right|}f_{i-1, k}+\sum\limits_{(x, y), x=x_{i}}|Y-y| $
同樣,設 \(F_{i}(x)=f_{i, x}, G_{i}(x)=\sum\limits_{x-\left|x_{i}-x_{i-1}\right| \leq k \leq x+\left|x_{i}-x_{i-1}\right|} f_{i-1, k}\)
那么 \(F_{i}(x)=G_{i}(x)+\sum_{\left(x^{\prime}, y^{\prime}\right), x^{\prime}=x_{i}}\left|x-y^{\prime}\right|\)
主要問題在於 \(G_i(x)\) 的維護,是取一個區間范圍 \([L,R]\) 內的最小值。
若斜率為 \(0\) 的兩端點在 \([L,R]\) 內,那么直接取最小值即可。
若斜率為 \(0\) 的兩端點在 \(L\) 左側,需要取 \(L\) 處的值作為最小值。
若斜率為 \(0\) 的兩端點在 \(R\) 右側,需要取 \(R\) 處的值作為最小值。
因而,需要維護斜率為 \(0\) 的折線的兩側分割點 \((a,b)\) ,同時還需要支持從斜率為 \(0\) 處向兩側訪問,因而使用小根堆與大根堆分別維護 \(b\) 右側以及 \(a\) 左側的點。
每次添加新的分割點時,根據新分割點與 \(a,b\) 的大小關系決定插入小根堆or大根堆,同時調整 \(a,b\) ,每次調整復雜度是 \(\mathcal{O}(1)\) 的(從小根堆中取出塞入大根堆或反之)
【AC Code】借用 jiangly的代碼
#include <bits/stdc++.h>
using i64 = long long;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n;
std::cin >> n;
std::vector<std::pair<int, int>> a;
for (int i = 0; i < n; i++) {
int x, y;
std::cin >> x >> y;
a.emplace_back(x + y, x);
}
std::priority_queue<i64> hl;
std::priority_queue<i64, std::vector<i64>, std::greater<>> hr;
for (int i = 0; i < n + 5; i++) {
hl.push(0);
hr.push(0);
}
i64 tag = 0, mn = 0;
int last = 0;
std::sort(a.begin(), a.end());
for (auto [s, x] : a) {
int d = s - last;
last = s;
tag += d;
if (x <= hl.top()) {
mn += hl.top() - x;
hl.push(x);
hl.push(x);
hr.push(hl.top() - tag);
hl.pop();
} else if (x >= hr.top() + tag) {
mn += x - (hr.top() + tag);
hr.push(x - tag);
hr.push(x - tag);
hl.push(hr.top() + tag);
hr.pop();
} else {
hl.push(x);
hr.push(x - tag);
}
}
std::cout << mn << "\n";
return 0;
}
