比賽鏈接：Here
1559A. Mocha and Math
題意：
給定一個區間，選擇區間內的值執行 & 操作使得區間最大值最小化
觀察樣例發現：令 x = (1 << 30) - 1 后 \(x\&a_0\& a_1\&...a_{n-1} =\) 答案
證明：
我們假設答案是 x。 在它的二進制表示中，只有在所有 \(a_i\) 的二進制表示中該位為 \(1\) 時，該位才會為 \(1\) 。否則，我們可以使用一個操作使 x 中的該位變為 \(0\) ，這是一個較小的答案。
所以我們可以初始設置 \(x=0\) 或者 \(x = 2^n -1\) 。 然后我們對序列進行迭代，使 \(x=x\&a_i\) ，最終 x 是 anwser。
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n;
cin >> n;
int x = (1 << 30) - 1;
for (int i = 0, a; i < n; ++i) {
cin >> a;
x &= a;
}
cout << x << "\n";
}
1559B.Mocha and Red and Blue
根據貪心思想，找到第一個非 ? 的下標，然后根據下標位置的值去枚舉情況即可
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int _; for (cin >> _; _--;) {
int n; string s;
cin >> n >> s;
for (int i = 0; i < n; ++i)
if (s[i] == '?' and i and s[i - 1] != '?')
s[i] = 'R' ^ 'B' ^ s[i - 1];
if (s.back() == '?') s.back() = 'R';
for (int i = n - 2; i >= 0; --i)
if (s[i] == '?') s[i] = 'R' ^ 'B' ^ s[i + 1];
cout << s << "\n";
}
}
1559C.Mocha and Hiking
路線規律題，
如果 \(a_1 = 1\) 那么路徑肯定有 \([(n + 1)\to 1\to2\to...\to n]\)
如果 \(a_n = 0\) 那么路徑為 \([1\to2\to...\to n\to (n + 1)]\)
對於其他情況來說：由於 \(a_1=0∧a_n =1\) ，所以肯定存在整數 \(i\) 使得 \(a_i =0∧a_{i + 1}=1\) ,那么路徑為 \([1\to 2\to...\to i\to(n + 1)\to (i + 1)\to (i + 2)\to...\to n]\)
具體證明可以參考哈密頓路徑
const int N = 1e4 + 10;
int a[N];
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int _; for (cin >> _; _--;) {
int n; cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
int idx = n;
for (int i = 1; i < n; ++i)
if (a[i] == 0 and a[i + 1] == 1) {
idx = i; break;
}
if (a[1] == 1) {
cout << n + 1 << " ";
for (int i = 1; i <= n; ++i) cout << i << " \n"[i == n];
continue;
}
for (int i = 1; i <= idx; ++i)
cout << i << " ";
cout << n + 1 << " ";
for (int i = idx + 1; i <= n; ++i) cout << i << " ";
cout << "\n";
}
}
1559D1.Mocha and Diana (Easy Version)
D1是一個暴力枚舉 + 並查集的裸題，D2就懵逼了，不知道怎么維護
兩個森林，同時加邊后還是森林，求最多加多少邊。
並查集，如果兩個森林中，i和j兩個節點都不在同一個集合中。加邊 i--j
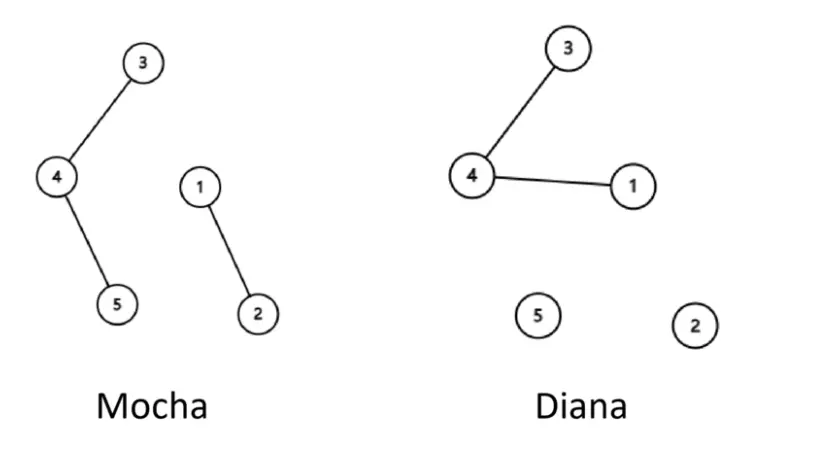
比如上圖左邊1和5不在一個集合，右邊1和5也不在一個集合，加邊1-5即可
const int N = 2e3 + 10;
int f1[N], f2[N];
int find1(int x) {return f1[x] == x ? x : f1[x] = find1(f1[x]);}
int find2(int x) {return f2[x] == x ? x : f2[x] = find2(f2[x]);}
void merge1(int x, int y) { f1[find1(x)] = find1(y);}
void merge2(int x, int y) { f2[find2(x)] = find2(y);}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n, m1, m2;
cin >> n >> m1 >> m2;
for (int i = 1; i <= n; ++i) f1[i] = f2[i] = i;
for (int i = 1, u, v; i <= m1; ++i) {
cin >> u >> v;
merge1(u, v);
}
for (int i = 1, u, v; i <= m2; ++i) {
cin >> u >> v;
merge2(u, v);
}
cout << min(n - m1 - 1, n - m2 - 1) << "\n";
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j) {
if (j == i) continue;
if (find1(i) != find1(j) && find2(i) != find2(j)) {
f1[find1(i)] = find1(j);
f2[find2(i)] = find2(j);
cout << i << " " << j << '\n';
}
}
}
1559D2. Mocha and Diana (Hard Version)
參考 B站up主 愛打CF的小趙同學
下面，我們稱兩個森林為左森林和右森林
如下圖
左森林1和2連接
右森林1和4連接
首先，對於左森林和右森林中的某個節點j，同時和節點1不在一棵樹上，即左森林中1和j不在一棵樹上，右森林中1和j不在一棵樹上。
那么就在兩個森林中將1和j連接。
左森林和右森林中，節點1和節點3都不在一棵樹上，連接1 3這條邊，如圖
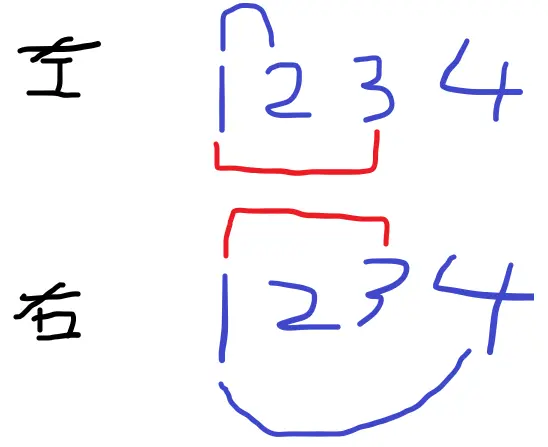
連接之后，還有一類節點可以連接，左森林的i和右森林的j。i和j滿足以下條件：
左森林中，1和i在一棵樹上，1和j不在一棵樹上 ；在右森林中，1和i不在一棵樹上，1和j在一棵樹上
類似於
節點2在左森林和1相連，節點4在右森林和1相連，則連接2 4 如圖
struct DSU {
vector<int> f, siz;
DSU(int n) : f(n), siz(n, 1) {iota(f.begin(), f.end(), 0);}
int find(int x) {return x == f[x] ? x : f[x] = find(f[x]);}
bool same(int x, int y) {return find(x) == find(y);}
bool merge(int x, int y) {
x = find(x), y = find(y);
if (x == y) return false;
siz[x] += siz[y];
f[y] = x;
return true;
}
int size(int x) {return siz[find(x)];}
};
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n, m1, m2;
cin >> n >> m1 >> m2;
DSU f1(n), f2(n);
for (int i = 0, u, v; i < m1; ++i) {
cin >> u >> v;
--u, --v;
f1.merge(u, v);
}
for (int i = 0, u, v; i < m2; ++i) {
cin >> u >> v;
--u, --v;
f2.merge(u, v);
}
int ans = n - 1 - max(m1, m2);
cout << ans << "\n";
vector<int> v1[n], v2[n];
while (ans > 0) {
for (int i = 0; i < n; ++i) v1[i].clear(), v2[i].clear();
for (int i = 0; i < n; ++i) {
v1[f1.find(i)].push_back(i);
v2[f2.find(i)].push_back(i);
}
int i = 0, j = 0;
while (1) {
while (i < n && f1.find(i) != i) i += 1;
while (j < n && f2.find(j) != j) j += 1;
if (i == n || j == n) break;
int a = -1, b = -1, c = -1, d = 0;
for (auto x : v1[i]) {
if (!f2.same(x, j)) a = x;
else c = x;
}
for (auto x : v2[j]) {
if (!f1.same(x, i)) b = x;
else c = x;
}
if (a != -1 && b != -1) {
cout << a + 1 << " " << b + 1 << "\n";
f1.merge(a, b);
f2.merge(b, a);
} else {
while (f1.same(d, i) || f2.same(d, j)) d += 1;
cout << c + 1 << " " << d + 1 << "\n";
f1.merge(c, d);
f2.merge(c, d);
}
ans -= 1;
i += 1, j += 1;
}
}
}
1559E. Mocha and Stars
E題在賽時沒想到正解，現在學習一下官方的題解
說實話，似乎E題在多校見過？
首先讓我們忽略 \(\gcd\) 的限制，令 \(f([l_1,l_2,...,l_n],[r_1,r_2,...,r_n],M)\) 為整數 \((a_1,a_2,..,a_n)\) 的個數滿足以下兩個條件
- \(\sum\limits_{i=1}^na_i\le m\)
- 對於所有的
i，\(a_i\) 都在 \([l_i,r_i]\) 范圍之間
所以我們可以通過前綴和優化背包DP來達到在 \(\mathcal{O}(nM)\) 內完成計算
此時再來考慮 \(\gcd\) 的約束條件，設 \(μ(n)\) 為莫比烏斯函數，\(g(a_1,a_2,…,a_n)\)為 \(1\) ，如果\((a_1,a_2,⋯,a_n)\) 滿足我們提到的兩個條件（沒有 \(\gcd\) 的約束），否則為 \(0\) 。
我們想要的答案是：
\[\begin{array}{ll} \sum\limits_{a_1=l_1}^{r_1}\sum\limits_{a_2=l_2}^{r_2}...\sum\limits_{a_n=l_n}^{r_n}[\gcd(a_1,a_2,...,a_n)=1]g(a_1,a_2,...,a_n) \\ = \sum\limits_{a_1=l_1}^{r_1}\sum\limits_{a_2=l_2}^{r_2}...\sum\limits_{a_n=l_n}^{r_n}g(a_1,a_2,...,a_n)\sum\limits_{d|\gcd(a_1,a_2,...,a_n)}μ(d)\\ =\sum\limits_{a_1=l_1}^{r_1}\sum\limits_{a_2=l_2}^{r_2}...\sum\limits_{a_n=l_n}^{r_n}g(a_1,a_2,...,a_n)\sum\limits_{d|a_1,d|a_2,..,d|a_n}μ(d)\\ =\sum\limits_{d=1}^Mμ(d)\sum\limits_{a_1=⌈\frac{l_1}d⌉}^{⌊\frac{r_1}d⌋}...\sum\limits_{a_n=⌈\frac{l_n}d⌉}^{⌊\frac{r_n}d⌋} g(a_1d,a_2d,...,a_nd) \end{array} \]
因為 \(\sum\limits_{i = 1}^n a_id\le M\) 可以被改寫成 \(\sum_{i=1}^na_i\le ⌊\frac Md⌋\) ,等價於
\[\sum\limits_{d=1}^Mμ(d)f(⌈\frac {l_1}d⌉,...,⌈\frac {l_n}d⌉,⌊\frac {r_1}d⌋,...,⌊\frac {r_n}d⌋,⌊\frac Md⌋) \]
時間復雜度：\(\mathcal{O}(n\sum\limits_{i=1}^M⌊\frac Mi⌋) = \mathcal{O}(nM\ log\ M)\)
#define maxn 100086
const int p = 998244353;
int n, m;
int l[maxn], r[maxn];
int f[maxn], sum[maxn];
int cal(int d) {
int M = m / d;
f[0] = 1;
for (int i = 1; i <= M; i++) f[i] = 0;
for (int i = 1; i <= n; i++) {
int L = (l[i] + d - 1) / d, R = r[i] / d;
if (L > R) return 0;
for (int j = 0; j <= M; j++) sum[j] = (f[j] + (j ? sum[j - 1] : 0)) % p;
for (int j = 0; j <= M; j++) {
f[j] = ((j - L >= 0 ? sum[j - L] : 0) + p - (j - R - 1 >= 0 ? sum[j - R - 1] : 0)) % p;
}
}
int ans = 0;
for (int i = 1; i <= M; i++) ans = (ans + f[i]) % p;
return ans;
}
int prm[maxn], cnt, mu[maxn];
bool tag[maxn];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> l[i] >> r[i];
mu[1] = 1;
for (int i = 2; i <= m; i++) {
if (!tag[i]) prm[++cnt] = i, mu[i] = p - 1;
for (int j = 1; j <= cnt && prm[j] * i <= m; j++) {
tag[i * prm[j]] = true;
if (i % prm[j]) mu[i * prm[j]] = (p - mu[i]) % p;
else break;
}
}
int ans = 0;
for (int i = 1; i <= m; i++) ans = (ans + 1ll * mu[i] * cal(i)) % p;
cout << ans;
}
最后在看H神的代碼時發現另外的一個代碼思路
const int mod = 998244353;
void add(int &u, int v) {
u += v;
if (u >= mod) u -= mod;
}
void sub(int &u, int v) {
u -= v;
if (u < 0) u += mod;
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n, m; cin >> n >> m;
vector<int> l(n), r(n);
vector<int> np(m + 1), ans(m + 1), p;
for (int i = 0; i < n; i += 1) cin >> l[i] >> r[i];
for (int i = 2; i <= m; i += 1) {
if (not np[i]) {
p.push_back(i);
for (int j = i * 2; j <= m; j += i) np[j] = 1;
}
}
for (int i = 1; i <= m; i += 1) {
vector<int> L(n), R(n);
int M = m / i, ok = 1;
for (int j = 0; j < n; j += 1) {
L[j] = (l[j] + i - 1) / i;
R[j] = r[j] / i;
if (L[j] > R[j]) ok = 0;
M -= L[j];
R[j] -= L[j];
}
if (not ok or M < 0) continue;
vector<int> dp(M + 1);
dp[0] = 1;
for (int j = 0; j < n; j += 1) {
for (int i = 1; i <= M; i += 1) add(dp[i], dp[i - 1]);
for (int i = M; i >= 0; i -= 1)
if (i > R[j]) sub(dp[i], dp[i - R[j] - 1]);
}
for (int x : dp) add(ans[i], x);
}
for (int x : p)
for (int i = 1; i * x <= m; i += 1)
sub(ans[i], ans[i * x]);
cout << ans[1];
}