比賽鏈接:Here
A - Alice and Bob (Game,打表)
emmm,博弈簽到題
題意:
Alice(先手) 和 Bob 面前有兩堆石頭,石頭數量為 \(n\) 和 \(m\)。
每次操作可從一堆石頭中取出 \(k\) 塊石頭,在另一堆石頭中取出 \(s\times k\) 塊。
哪一方無法執行操作則判負
我們知道當面臨兩堆石頭數量為(0,0)時為失敗,那么如果能一次操作能取光石頭此時為必勝態
我們用一個二維數組 \(f[i][j]\) 來表示第一堆石頭數量為i第二堆石頭數量為j的情況,\(f[i][j]=1\) 表示狀態面臨兩堆石頭數量為 \(i,j\) 時可以一步取光石頭,\(f[i][j]=0\) 表示狀態面臨兩堆石頭數量為 \(i,j\) 時無法一次取光石頭。初始 \(f[0][0]=0\) ,根據題目 \(f[k][s*k]\) 或 \(f[s*k][k]\) 一定能夠一次性取完,我們可以從(\(i=0,j=0\) )開始自小變大枚舉 \(s\) 與 \(k\) 找出所有先手必勝的狀態,由於是自小變大枚舉所以發現有\(f[i][j]=0\) 就發現了一個必敗的局面再對它枚舉 \(s\) 與 \(k\) ,當初始狀態 \(f[i][j]=1\) 時 Alice 顯然獲勝,那么現在面臨的問題是當初始狀態為 \(f[i][j]=0\) 時 Alice 能否獲勝,由於 Alice 一次取不完石頭,又要保證自己一次取完后不輸,即需要滿足取完石子后 \(f[i-k][j-s*k]=0\) 或者 \(f[i-s*k][j-k]=0\),這顯然是不可能的,因為對於每一個 \(f[i][j]==0\) 其 \(f[i+k][j+s*k]=1\)(同 \(f[0][0]\) ),時間復雜度為\(O(n^4)\),顯然不滿足題目數據,但是這里大家需要知道一個結論:對於一個的 \(i\) 只存在至多一種 \(j\) 后手能夠獲勝
證明如下:
若存在 \((i,q)(i,p)\)(p>q)滿足后手勝,那么Alice只需將(i,p)->(i,q)即可獲勝,不滿足后手勝的條件。
這樣我們的時間復雜度大約在 \(O(n^3)\),本題數據量為 \(5000\),勉勉強強過的去,但是需要避免cin等操作,數組也需要開成 bool 的來節省運算時間。
【AC Code】
#include<iostream>
#include<stdio.h>
using namespace std;
bool f[5010][5010] = {false};
int main() {
// cin.tie(nullptr)->sync_with_stdio(false);
//自小到大枚舉i,j
for (int i = 0; i <= 5000; i++)
for (int j = 0; j <= 5000; j++) {
if (f[i][j] == 0) { //對於每種必敗態進行拓展
//f[i][j]與f[j][i]是等價的
for (int k = 1; k + i <= 5000; k++)for (int s = 0; s * k + j <= 5000; s++)f[i + k][j + s * k] = 1;
for (int k = 1; k + j <= 5000; k++)for (int s = 0; s * k + i <= 5000; s++)f[i + s * k][j + k] = 1;
}
}
int n, m, t;
scanf("%d", &t);
while (t--) {
scanf("%d%d", &n, &m);
if (!f[n][m])puts("Bob");
else puts("Alice");
}
}
看了下其他人的代碼,個個打表也是神了
B - Ball Dropping (Math)
給一個中間空的等腰梯形。
然后有一個圓,問是否能從中間穿過梯形。
借用 純神 的說法:
這道題是一個數學題,簡單畫個圖即可
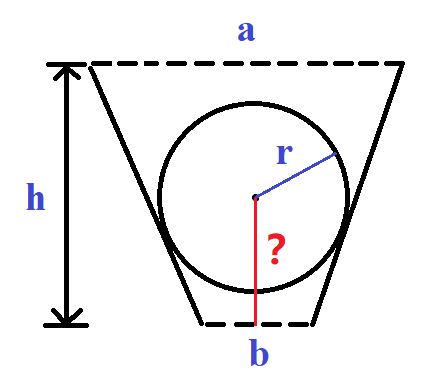
看到梯形我們考慮用相似三角。
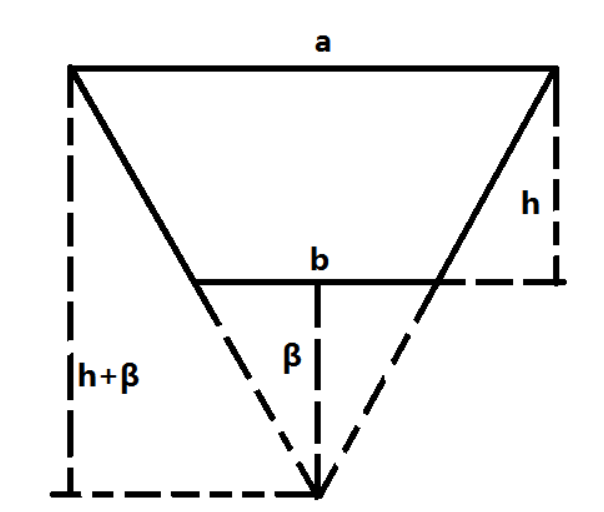
首先兩個相似求出 \(\beta: \frac{b}{a} = \frac{\beta}{h + \beta}\)
\(\beta = \frac{bh}{a - b}\)
然后由於它是等腰,我們可以繼續求。
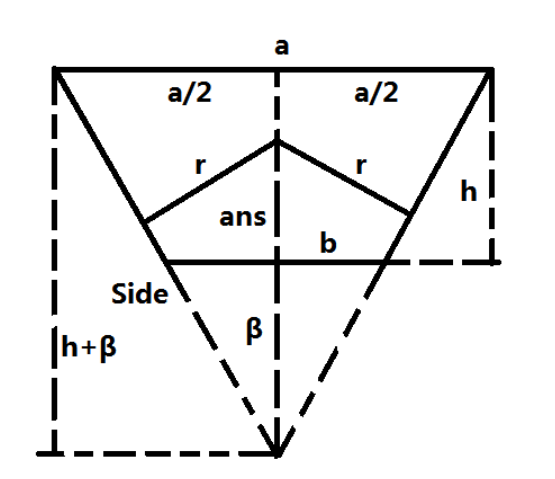
(注意這個球掉到上面的地方與牆面碰到的兩個點組成的直線不是直徑)
(我當時就搞錯了,搞了半天才發現,兩個牆壁是它的切線)
用勾股可以得到 \(Side = \sqrt{(a/2)^2 + (h + \beta)^2}\)
然后根據相似,可以得到 \(\beta + ans\)
\(a/2=\frac{Side}{ans + \beta + ans}\\ans+\beta = \frac{r * Side}{a/2}\\ans = \frac{r * Side}{a/2} - \beta\)
【AC Code】
using ld = long double;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
ld r, a, b, h;
scanf("%Lf %Lf %Lf %Lf", &r, &a, &b, &h);
if (a < b) swap(a, b);
if ((r * 2.0) <= b) printf("Drop");
else {
printf("Stuck\n");
ld beta = b * h / (a - b);
ld side = sqrt((a / 2) * (a / 2) + (beta + h) * (beta + h));
printf("%Lf", side * r / (a / 2) - beta);
}
}
C - Cut the Tree
待補
D - Determine the Photo Position (簽到)
題意:
給出一個矩陣,問有多少個地方有連續的 \(x\) 個 \(0\),一定要在一行中。
暴力模擬枚舉,
記錄一個 \(num\) 為當前這一行最后出現了多少個連續的 \(0\),那如果接下來是 \(0\),就 \(num\) 加一,否則就變成 \(0\)。
然后每次搞完看一下,如果 \(num\) 大於等於 \(m\) 就答案加一,表示以這個點結束的一個位置是連續的 \(x\) 個 \(0\)。
【AC Code】
int main() {
// cin.tie(nullptr)->sync_with_stdio(false);
int n, m;
cin >> n >> m;
int a[n + 1][n + 1], ans = 0;
for (int i = 1; i <= n; ++i) {
int num = 0;
for (int j = 1; j <= n; ++j) {
scanf("%1d", &a[i][j]);
if (a[i][j] == 0)num++;
else num = 0;
if (num >= m)ans++;
}
}
cout << ans << "\n";
}
E - Escape along Water Pipe
待補
F - Find 3-friendly Integers (簽到)
題意:
3-friendly定義:一個正整數的各個位數能整除 3 則稱這個數為 3-friendly.
比如,104中 0 可整除 3,124中 12 可整除 3
問在區間 \(【L,R】\) 中有多少個 3-friendly.
這個很容易知道三位數以上的值隨便組合都能整除 3
所以我們可以先序找出 1 ~ 100 中所有非 3-friendly 的數,然后在區間計數時刪去即可
【AC Code】記得使用 long long
using ll = long long;
int vis[] = {1, 2, 4, 5, 7, 8, 11, 14, 17, 22, 25, 28, 41, 44, 47, 52, 55, 58, 71, 74, 77, 82, 85, 88};
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int _; for (cin >> _; _--;) {
ll l, r, k = 0;
cin >> l >> r;
for (int i = 0; i < 24; ++i) {
if (vis[i] >= l and vis[i] <= r)k++;
}
cout << r - l + 1 - k << "\n";
}
}
G - Game of Swapping Numbers
題意:
給兩個數組a,b,現在可以交換a中的數k次,求 \(\sum\limits_{i = 1}^n|a_i - b_i|\)的最大值。
首先我們思考一下什么樣的兩個數交換后的結果會大:
假如有兩對數: \((a_1,b_1),(a_2,b_2)\)
原結果為 \(abs(a_1-b_1)+abs(a_2-b_2)\)
- 如果 \(a_1>b_1\) && $a_2>b_2 $&& \(b_1>a_2\) :
那么原結果為 \(abs(a_1-b_1)+abs(a_2-b_2)=a_1+a_2-b_1-b_2\)
交換后結果為:\(abs(a_1-b_1)+abs(a_2-b_2)=a_1-b_2+b_1-a_2=a_1+b_1-a_2-b_2\)
結果之差為 \(2 * b_1 - 2 * a_2=2*min(a_1,b_1)-2 * max(a_2,b_2)\) - 如果 \(a_1>b_1\) && \(a_2>b_2\) && \(b_1 < a_2\) :
那么原結果為 \(abs(a_1-b_1)+abs(a_2-b_2)=a_1+a_2-b_1-b_2\)
交換后結果為:\(abs(a_1-b_2)+abs(a_2-b_1)=a_1-b_2+a_2-b_1=a_1+a_2-b_1-b_2\)
結果之差為 \(0\)
如此分析下去:
我們發現可以使結果增長的情況為一對的最小值大於另一對的最大值時.
然后當 \(n> 2\) 時,最優解結果\((a1,b1),(a2,b2),(a3,b3).........\)其中 \(a_i<b_i\) 或者 \(a_i>b_i\) 的對數一定有一種有兩對,假如這兩對為$(a1,b1),(a2,b2) $ {\(a_1>b_1\) && \(a_2>b_2\)}如上分析要么增加要么不變,所以恰好為 \(k\) 在 \(n>2\) 時等價於小於等於 \(k\) 次,所以加上可以增加的情況並小於等於 \(k\) 次即可。
【AC Code】
const int N = 5e5 + 7;
ll a[N], b[N], Ma[N], Mi[N];
bool cmp(ll a, ll b) { return a > b;}
int main() {
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
ll ans = 0;
if (n == 2) {
if (k % 2) swap(a[1], a[2]);
ans = ans + abs(a[1] - b[1]) + abs(a[2] - b[2]);
} else {
for (int i = 1; i <= n; i++) {
ans = ans + abs(a[i] - b[i]);
Ma[i] = max(a[i], b[i]);
Mi[i] = min(a[i], b[i]);
}
sort(Mi + 1, Mi + n + 1, cmp);
sort(Ma + 1, Ma + n + 1);
for (int i = 1; i <= k && i <= n; i++) {
if (Mi[i] > Ma[i]) ans = ans + 2 * (Mi[i] - Ma[i]);
else break;
}
}
cout << ans << endl;
return 0;
}
H - Hash Function
待補
I - Increasing Subsequence (DP)
題意:
給定一個長度為 \(n(n<=5000)\) 的排列,兩個人輪流從這個序列中選擇一個數,要求當前回合此人選擇的數大於任意一個已經被選擇的數,並且該數在數組中的位置 \(i\) 與此人上一次選擇的數在數組中的位置 \(j\) 要滿足 \(i>j\),如果有多個數合法則等概率的從這些數中選一個。當沒有合法數時結束,問最終被選擇的數的期望個數。
思路:
期望 \(dp\) 問題,設 \(dp[x][y]\) 為當前輪到此人選數並且他上一次選了數 \(x\) ,另一個人選了數 \(y\) 開始游戲到游戲結束時的數期望個數,則 \(dp[x][y] = inv[tot] * \sum\limits_{t=1}^{tot} + 1\), \(tot\) 為可選擇的數字個數,\(a_i\) 為可選的數字。首先枚舉 \(y\) ,然后用前綴和處理即可 \(\mathcal{O}(1)\) 完成轉移,再枚舉 \(x\) ,總復雜度為 \(\mathcal{O}(n^2)\) 。
【AC Code】
const int mod = 998244353, N = 5e3 + 10;
int p[N], c[N], sum[N], pos[N], inv[N];
int dp[N][N];
int qpow(int a, int b) {
int ans = 1;
for (; b; b >>= 1, a = 1ll * a * a % mod)
if (b & 1)ans = 1ll * ans * a % mod;
return ans;
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n;
cin >> n;
for (int i = 1; i <= n; i += 1) {
cin >> p[i];
pos[p[i]] = i;
inv[i] = qpow(i, mod - 2);
}
for (int j = n; j > 0; j -= 1) {
for (int i = 0; i <= n; i += 1) c[i] = sum[i] = 0;
for (int t = j + 1; t <= n; t += 1) {
c[pos[t]] = 1;
sum[pos[t]] = dp[j][t];
}
for (int i = n - 1; i >= 0; i -= 1) {
c[i] += c[i + 1];
sum[i] = (sum[i] + sum[i + 1]) % mod;
}
for (int i = j - 1; i >= 0; i -= 1) {
int tot = c[pos[i]];
int sm = sum[pos[i]];
if (tot) dp[i][j] = (1ll * inv[tot] * sm + 1) % mod;
}
}
ll ans = 0;
for (int i = 1; i <= n; i += 1)ans = (ans + dp[0][i]) % mod;
cout << (1ll * ans * inv[n] % mod + 1) % mod;
}
J - Journey among Railway Stations
待補
K - Knowledge Test about Match
待補
