閱讀之前看這里
👉:博主是正在學習數據分析的一員,博客記錄的是在學習過程中一些總結,也希望和大家一起進步,在記錄之時,未免存在很多疏漏和不全,如有問題,還請私聊博主指正。
博客地址: 天闌之藍的博客
,學習過程中不免有困難和迷茫,希望大家都能在這學習的過程中肯定自己,超越自己,最終創造自己。
統計學的知識,學了那么多,應該在實際問題去驗證和解決,盡量在實際項目中去應用,要有輸出的環境,否則學習只是學習,並不能檢驗真正的水平和意義。所以針對此,后續在網上找一些案例進行實操。
案例1
例1:某互聯網公司希望激活數量可觀的沉默用戶,設計了3個方案,將所有沉默用戶隨機分布在規模相同的三個群中,將3套方案實施在這3個群體中,觀察3個群體中每天成功喚醒的用戶數量,下圖是3個方案實施8天后的數據:
那么作為數據分析師,要如何依據上面的數據衡量每個喚醒方案的效果,選出最優方案呢?這個問題結合業務的分析,還是可以實現的。但是這里主要結合基本的統計學知識來做基本的分析。
分析方法有哪些呢:

我們 先假設這3個方案的用戶激活數的均值是相等的 。我們需 要通過統計學的方法來驗證這個假設是否正確
,如果滿足這個條件,則接受這個假設,說明這3個方案的效果是相同的,如果不滿足一定的條件,就拒絕這個假設,說明這個3個方案激活效果是不一樣的,那么才有接下來的深層分析。
這里我們對這3個方案的數據做了單因素方差分析:
STEP1 :在EXCEL2019中工具欄中選擇數據,然后選擇數據分析

STEP2 :選擇單因素方差分析
STEP3 :選擇輸入區域,這里默認輸出到新工作表,也可以選定區域輸出
選取下列數據

輸出結果:
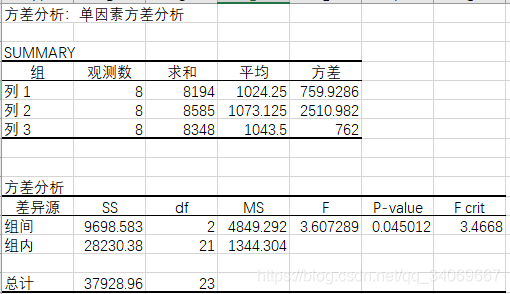
這樣我們就得到了單因素方差分析的結果了。
分析 :
MS值得是均方和,F指的是F檢驗統計量的值,P-value值得是出現當前結果的概率,說明的是,在原假設成立的前提下,3個方案均值分別的1024、1073、1043的
概率僅為0.045 , 低於顯著性概率0.05 ,如此小概率的事件在一次實驗中發生是不可能的, 因此要拒絕原假設 ,
也就說這3個方案所激活的沉默用戶的均值是不相同的 。
那到底是哪個方案最優呢?在證明了3個方案的效果均值不同之后,最簡單的方案就是看均值,均值最高的就是最優的方案,因此可以選擇 方案2 。
但是,我們都會知道, 均值反應的是數據的集中趨勢,數據還有波動性,如果方案2的均值最大 ,但是對應的 方差很大
,那依據均值來判斷就不是那么可靠了。
如果要精確對比出哪個方案最優,還 需要對這3個方案兩兩組合做T檢驗
,目的是對比兩個樣本是否來自均值相等的總體,也就是告訴你兩個樣本的均值差別是不是顯著的。

在這里我們選擇EXCEL中t-檢驗, 雙樣本等方差假設
通過T檢驗,我們得到了如下結果:
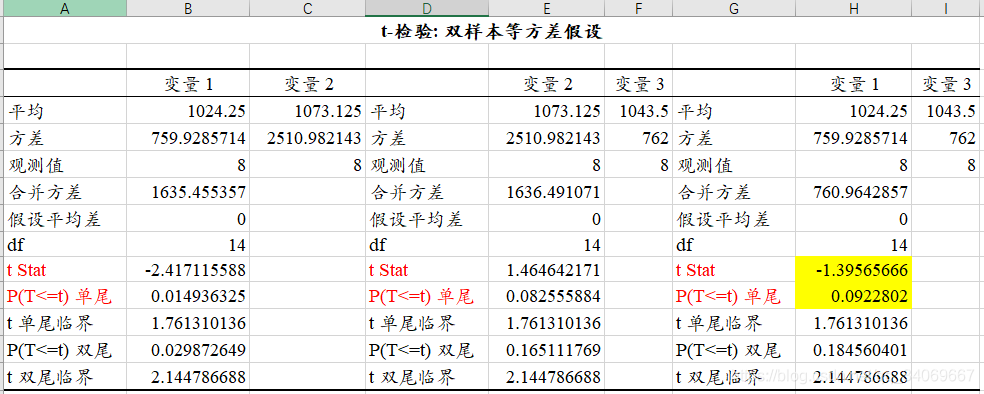
從輸出結果來看,不僅有單側t檢驗和雙側t檢驗結果:
t Stat :計算得出的t值;
**P(T <=t)單尾與t單尾臨界 ** :已知顯著水平下的單尾臨界t值和P值;
**P(T <=t)雙尾與t雙尾臨界 ** :已知顯著水平下的雙尾臨界t值和P值;
合並方差 :合並公式如下:
我們通過上圖發現,方案1和方案2之間呈現出了 顯著性 ,可以判斷 方案2是優於方案1的
,至於方案1和方案3,暫時沒有足夠的證據判斷他們的優劣。在這里呢,可以繼續用均值來做比較就會准確很多了。
案例2
案例2:
某互聯網公司開發了一個識別商家是否是惡性商戶的模型M1。在使用模型之前,人工監察團隊說,目前平台上的惡性商戶比率為0.2%。利用M1模型監測后,發現在之前人工判定的惡性商戶中,有模型判定為惡性商戶的人數占比為90%,在人工判定的健康商戶中,有M1判定為惡性商戶的人數占比為8%,通過這些分析會感覺商戶有8%的誤判,還有10%的漏判,那么這個模型的結果到底是不是可靠的呢?
在這里我們利用貝葉斯模型來做分析:預備知識 《商務與經濟統計》學習筆記(四)–貝葉斯定理之理解
- 平台上的惡性商戶比率為0.2%,記為 P ( E ) = 0.002 P(E) = 0.002 P ( E ) = 0 . 0 0 2 ,那么 P ( E ) = 0.998 P(~E)=0.998 P ( E ) = 0 . 9 9 8 。
- 模型M1所判定為陽性(惡性商戶)的人數占比為90%,這是一個條件概率,表示為 P ( P ∣ E ) = 0.9 P(P|E)=0.9 P ( P ∣ E ) = 0 . 9
- 在監察團隊判定為健康商戶群體中,由模型M1判定為陽性的人數占比為8%,表示為 P ( P ∣ E ) = 0.08 P(P|~E)=0.08 P ( P ∣ E ) = 0 . 0 8
利用全概率公式:
當M1判別某個商戶為惡性商戶時,這個商戶的確是惡性商戶的概率由 P ( E ∣ P ) P(E|P) P ( E ∣ P ) 表示:
P ( E ∣ P ) = P ( P ∣ E ) ∗ P ( E ) P ( E ) ∗ P ( P ∣ E ) + P ( E ) ∗ P ( P ∣
E ) P(E|P)=\dfrac{P(P|E)P(E)}{P(E)P(P|E)+P(E)*P(P|E)} P ( E ∣ P ) =
P ( E ) ∗ P ( P ∣ E ) + P ( E ) ∗ P ( P ∣ E ) P ( P
∣ E ) ∗ P ( E )
上面就是全概率公式。要知道判別為惡性商戶的前提下,該商戶實際為惡性商戶的概率,需要由先前的惡性商戶比率 P ( E ) P(E) P ( E )
,以判別的惡性商戶中的結果為陽性的商戶比率 P ( P ∣ E ) P(P|E) P ( P ∣ E )
,以判別為健康商戶中的結果為陽性的比率 P ( P ∣ E ) P(P|~E) P ( P ∣ E ) ,以判別商戶中健康商戶的比率 P
( E ) P(~E) P ( E ) 來共同決定:
P ( E ) = 0.002 P(E)=0.002 P ( E ) = 0 . 0 0 2 P ( P ∣ E ) = 0.9
P(P|E) =0.9 P ( P ∣ E ) = 0 . 9 P ( E ) = 0.998 P(~E)=0.998 P (
E ) = 0 . 9 9 8 P ( P ∣ E ) = 0.08 P(P|~E)=0.08 P ( P ∣ E ) =
0 . 0 8 P ( E ∣ P ) = P ( P ∣ E ) ∗ P ( E ) / ( P ( E ) ∗ P ( P ∣ E ) + P
( E ) ∗ P ( P ∣ E ) ) = 0.022 P(E|P)= P(P|E)P(E) /
(P(E)P(P|E)+P(E)*P(P|E)) =0.022 P ( E ∣ P ) = P ( P ∣ E ) ∗
P ( E ) / ( P ( E ) ∗ P ( P ∣ E ) + P ( E ) ∗ P ( P
∣ E ) ) = 0 . 0 2 2
通過貝葉斯模型計算,惡性商戶的比例為2.2%,也就是說,根據M1的判別結果,某個商戶實際為惡性商戶的概率為2.2%,是不進行模型判別的11倍。
雖然2.2%的概率並不算高,但在實際情況中,被M1模型判別為惡性商戶,說明這家商戶做出惡性行為的概率是一般商戶的11倍,非常有必要用進一步的手段檢查。
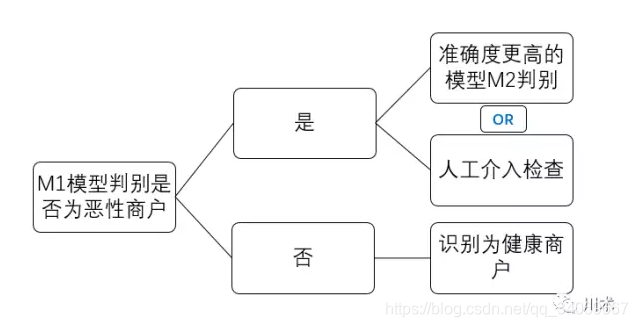
惡性商戶判別模型真正的使用邏輯應該是如下圖所示。我們先用M1進行一輪判別,結果是陽性的商戶,說明出現惡性行為的概率是一般商戶的11倍,那么有必要用精度更高的方式進行判別,或者人工介入進行檢查。精度更高的檢查和人工介入,成本都是非常高的。因此M1模型的使用能夠使我們的成本得到大幅節約。
貝葉斯模型在很多方面都有應用,我們熟知的領域就有垃圾郵件識別、文本的模糊匹配、欺詐判別、商品推薦等等。通過貝葉斯模型的闡述,大家應該有這樣的一種體會:分析模型並不取決於多么復雜的數學公式,多么高級的軟件工具,多么高深的算法組合;它們的原理往往是通俗易懂的,實現起來也沒有多高的門檻。比如貝葉斯模型,用Excel的單元格和加減乘除的符號就能實現。所以,不要覺得數據分析建模有多遙遠,其實就在你手邊。



