時間序列預測之 AUTO-ARIMA

參考鏈接：常用7種時間序列預測模型

                  用python做時間序列預測九：ARIMA模型簡介

運用ARIMA進行時間序列建模的基本步驟：

• 1）加載數據：構建模型的第一步當然是加載數據集。
• 2）預處理：根據數據集定義預處理步驟。包括創建時間戳、日期/時間列轉換為d類型、序列單變量化等。
• 3）序列平穩化：為了滿足假設，應確保序列平穩。這包括檢查序列的平穩性和執行所需的轉換。
• 4）確定d值：為了使序列平穩，執行差分操作的次數將確定為d值。
• 5）創建ACF和PACF圖：這是ARIMA實現中最重要的一步。用ACF PACF圖來確定ARIMA模型的輸入參數。
• 6）確定p值和q值：從上一步的ACF和PACF圖中讀取p和q的值。
• 7）擬合ARIMA模型：利用我們從前面步驟中計算出來的數據和參數值，擬合ARIMA模型。
• 8）在驗證集上進行預測：預測未來的值。
• 9）計算RMSE：通過檢查RMSE值來檢查模型的性能，用驗證集上的預測值和實際值檢查RMSE值。

 

ARMA模型公式：

       

  

信息准則定階

• AIC(Akaike Information Criterion)

         
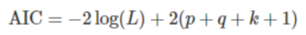
           L是數據的似然函數，k=1表示模型考慮常數c，k=0表示不考慮。最后一個1表示算上誤差項，所以其實第二項就是2乘以參數個數。

• AICc（修正過的AIC）

         

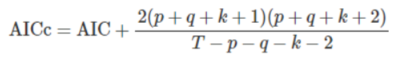
• BIC(Bayesian Information Criterion)

        

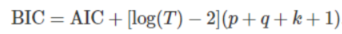
注意事項： 

• 信息准則越小，說明參數的選擇越好，一般使用AICc或者BIC。
• 差分d，不要使用信息准則來判斷，因為差分會改變了似然函數使用的數據，使得信息准則的比較失去意義，所以通常用別的方法先選擇出合適的d。
• 信息准則的好處是可以在用模型給出預測之前，就對模型的超參做一個量化評估，這對批量預測的場景尤其有用，因為批量預測往往需要在程序執行過程中自動定階。

 

數據平穩性檢驗

# 測試序列平穩性
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
	#Determing rolling statistics
	rolmean = timeseries.rolling(window=12).mean()
	rolstd = timeseries.rolling(window=12).std()
	#Plot rolling statistics:
	fig = plt.figure(figsize=(12, 8))
	orig = plt.plot(timeseries, color='blue',label='Original')
	mean = plt.plot(rolmean, color='red', label='Rolling Mean')
	std = plt.plot(rolstd, color='black', label = 'Rolling Std')
	plt.legend(loc='best')
	plt.title('Rolling Mean & Standard Deviation')
	plt.show()
	#Perform Dickey-Fuller test:
    #迪基-福勒檢驗還可以擴展為增廣迪基-福勒檢驗（Augmented Dickey-Fuller test），簡稱ADF檢驗，可檢驗模型是否存在單位根（unit root）
	print('Results of Dickey-Fuller Test:')
	dftest = adfuller(timeseries, autolag='AIC')
	dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
	for key,value in dftest[4].items():
    	dfoutput['Critical Value (%s)'%key] = value
    	print(dfoutput)

　　

要將非平穩時間序列轉為平穩序列，有如下幾種方法：

• Deflation by CPI
• Logarithmic（取對數）
• First Difference（一階差分）
• Seasonal Difference（季節差分）
• Seasonal Adjustment

這里會嘗試取對數、一階查分、季節差分三種方法，先進行一階差分，去除增長趨勢后檢測穩定性：

可以看到圖形上看上去變穩定了，但p-value的並沒有小於0.05。再來看看12階查分（即季節查分），看看是否穩定：
從圖形上，比一階差分更不穩定（雖然季節指標已經出來了），我們再來將一階查分和季節查分合並起來，再來看下：
可以看到，在一階差分后再加上季節差分，數據終於穩定下了。P-value小於了0.05，並且Test Statistic的值遠遠小於Critical Value (5%)的值。
對原始數據取對數有兩個用處：第一個是將指數增長轉為線性增長；第二可以平穩序列的方差
取對數后，從圖形上看有些穩定了，但p-value還是沒有接近0.05，沒能達穩定性要求。在此基礎上我們再來做下一階差分，去除增長趨勢：
還是沒能滿足需求，再來試試在對數基礎上進行一階差分+季節差分的效果：
可以看到穩定了滿足需求了，但是穩定性相比不取對數的情況下，並沒有提升而是下降了。

#原始序列
test_stationarity(df['riders'])
#一階差分
df['first_difference'] = df['riders'].diff(1)
test_stationarity(df['first_difference'].dropna(inplace=False))
#季節差分
df['seasonal_difference'] = df['riders'].diff(12)
test_stationarity(df['seasonal_difference'].dropna(inplace=False))
#一階差分+季節差分
df['seasonal_first_difference'] = df['first_difference'].diff(12)
test_stationarity(df['seasonal_first_difference'].dropna(inplace=False))
#對數
df['riders_log']= np.log(df['riders'])
test_stationarity(df['riders_log'])
#對數+一階差分
df['log_first_difference'] = df['riders_log'].diff(1)
test_stationarity(df['log_first_difference'].dropna(inplace=False))
#對數+季節差分
df['log_seasonal_difference'] = df['riders_log'].diff(12)
test_stationarity(df['log_seasonal_difference'].dropna(inplace=False))
#對數+一階差分+姐姐查分
df['log_seasonal_first_difference'] =df['log_first_difference'].diff(12)
test_stationarity(df['log_seasonal_first_difference'].dropna(inplace=False))

　　

 如何確定差分階數和常數項：

1.假如時間序列在很高的lag（10以上）上有正的ACF，則需要很高階的差分

2.假如lag-1的ACF是0或負數或者非常小，則不需要很高的差分，假如lag-1的ACF是-0.5或更小，序列可能overdifferenced。

3.最優的差分階數一般在最優階數下標准差最小（但並不是總數如此）

4.模型不查分意味着原先序列是平穩的；1階差分意味着原先序列有個固定的平均趨勢；二階差分意味着原先序列有個隨時間變化的趨勢

5.模型沒有差分一般都有常數項；有兩階差分一般沒常數項；假如1階差分模型非零的平均趨勢，則有常數項

 

如何確定AR和MA的階數：

1.假如PACF顯示截尾或者lag-1的ACF是正的（此時序列仍然有點underdifferenced），則需要考慮AR項；PACF的截尾項表明AR的階數

2.假如ACF顯示截尾或者lag-1的ACF是負的（此時序列有點overdifferenced），則需要加MA項，ACF的截尾項表明AR的階數

3.AR和MA可以相互抵消對方的影響，所以假如用AR-MA模型去擬合數據，仍然需要考慮加些AR或MA項。尤其在原先模型需要超過10次的迭代去converge。

假如在AR部分有個單位根（AR系數和大約為1），此時應該減少一項AR增加一次差分

假如在MA部分有個單位根（MA系數和大約為1），此時應該減少一項AR減少一次差分

假如長期預測出現不穩定，則可能AR、MA系數有單位根

 

如何確定季節性部分：

1.假如序列有顯著是季節性模式，則需要用季節性差分，但是不要使用兩次季節性差分或總過超過兩次差分（季節性和非季節性）

2.假如差分序列在滯后s處有正的ACF，s是季節的長度，則需要加入SAR項；假如差分序列在滯后s處有負的ACF，則需要加入SMA項，如果使用了季節性差異，則后一種情況很可能發生，如果數據具有穩定和合乎邏輯的季節性模式。如果沒有使用季節性差異，前者很可能會發生，只有當季節性模式不穩定時才適用。應該盡量避免在同一模型中使用多於一個或兩個季節性參數（SAR + SMA），因為這可能導致過度擬合數據和/或估算中的問題。

 

 模型構建

from statsmodels.tsa.arima_model import ARIMA

# 1,1,2 ARIMA Model
model = ARIMA(df.value, order=(1,1,2))
model_fit = model.fit(disp=0)
print(model_fit.summary())

 

 中間的表格列出了訓練得到的模型各項和對應的系數，如果系數很小，且‘P>|z|’ 列下的P-Value值遠大於0.05，則該項應該去掉，比如左圖中的ma部分的第二項，系數是-0.0010,P-Value值是0.998,那么可以重建模型為ARIMA(1,1,1)，從右圖可以看到，修改階數后的模型的AIC等信息准則都有所降低

 通常會檢查模型擬合的殘差序列，即訓練數據原本的序列減去訓練數據上的擬合序列后的序列。該序列越符合隨機誤差分布(均值為0的正態分布)，說明模型擬合的越好，否則，說明還有一些因素模型未能考慮。

# Plot residual errors
residuals = pd.DataFrame(model_fit.resid)
fig, ax = plt.subplots(1,2)
residuals.plot(title="Residuals", ax=ax[0])
residuals.plot(kind='kde', title='Density', ax=ax[1])
plt.show()

# Actual vs Fitted
model_fit.plot_predict(dynamic=False)
plt.show()

　　       

from statsmodels.tsa.stattools import acf

# Create Training and Test
train = df.value[:85]
test = df.value[85:]

# Build Model
model = ARIMA(train, order=(3,2,1))  
# model = ARIMA(train, order=(1, 1, 1))    #預測效果很差，選用上面的效果有提升
fitted = model.fit(disp=-1)  

# Forecast
fc, se, conf = fitted.forecast(15, alpha=0.05)  # 95% conf

# Make as pandas series
fc_series = pd.Series(fc, index=test.index)
lower_series = pd.Series(conf[:, 0], index=test.index)
upper_series = pd.Series(conf[:, 1], index=test.index)

# Plot
plt.figure(figsize=(12,5), dpi=100)
plt.plot(train, label='training')
plt.plot(test, label='actual')
plt.plot(fc_series, label='forecast')
plt.fill_between(lower_series.index, lower_series, upper_series, 
                 color='k', alpha=.15)
plt.title('Forecast vs Actuals')
plt.legend(loc='upper left', fontsize=8)
plt.show()

　　

  

 AUTO-ARIMA模型 （python - pmdarima；r - forecast）

通過預測結果來推斷模型階數的好壞畢竟還是耗時耗力了些，一般可以通過計算AIC或BIC的方式來找出更好的階數組合。pmdarima模塊的auto_arima方法就可以讓我們指定一個階數上限和信息准則計算方法，從而找到信息准則最小的階數組合。

from statsmodels.tsa.arima_model import ARIMA
import pmdarima as pm

df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names=['value'], header=0)

model = pm.auto_arima(df.value, start_p=1, start_q=1,
                      information_criterion='aic',
                      test='adf',       # use adftest to find optimal 'd'
                      max_p=3, max_q=3, # maximum p and q
                      m=1,              # frequency of series
                      d=None,           # let model determine 'd'
                      seasonal=False,   # No Seasonality
                      start_P=0, 
                      D=0, 
                      trace=True,
                      error_action='ignore',  
                      suppress_warnings=True, 
                      stepwise=True)

print(model.summary())

# Forecast
n_periods = 24
fc, confint = model.predict(n_periods=n_periods, return_conf_int=True)
index_of_fc = np.arange(len(df.value), len(df.value)+n_periods)

# make series for plotting purpose
fc_series = pd.Series(fc, index=index_of_fc)
lower_series = pd.Series(confint[:, 0], index=index_of_fc)
upper_series = pd.Series(confint[:, 1], index=index_of_fc)

# Plot
plt.plot(df.value)
plt.plot(fc_series, color='darkgreen')
plt.fill_between(lower_series.index, 
                 lower_series, 
                 upper_series, 
                 color='k', alpha=.15)

plt.title("Final Forecast of WWW Usage")
plt.show()

　　 

如何自動構建季節性ARIMA模型？

如果模型帶有季節性，則除了p,d,q以外，模型還需要引入季節性部分：

與非季節性模型的區別在於，季節性模型都是以m為固定周期來做計算的，比如D就是季節性差分，是用當前值減去上一個季節周期的值，P和Q和非季節性的p,q的區別也是在於前者是以季節窗口為單位，而后者是連續時間的。
上節介紹的auto arima的代碼中，seasonal參數設為了false，構建季節性模型的時候，把該參數置為True，然后對應的P，D，Q,m參數即可，代碼如下：

# !pip3 install pyramid-arima
import pmdarima as pm
# Seasonal - fit stepwise auto-ARIMA
smodel = pm.auto_arima(data, start_p=1, start_q=1,
                         test='adf',
                         max_p=3, max_q=3, m=12,
                         start_P=0, seasonal=True,
                         d=None, D=1, trace=True,
                         error_action='ignore',  
                         suppress_warnings=True, 
                         stepwise=True)
smodel.summary()

注意這里的stepwise參數，默認值就是True，表示用stepwise algorithm來選擇最佳的參數組合，會比計算所有的參數組合要快很多，而且幾乎不會過擬合，當然也有可能忽略了最優的組合參數。所以如果你想讓模型自動計算所有的參數組合，然后選擇最優的，可以將stepwise設為False。 

如何在預測中引入其它相關的變量？

 在時間序列模型中，還可以引入其它相關的變量，這些變量稱為exogenous variable(外生變量，或自變量)，比如對於季節性的預測，除了之前說的通過加入季節性參數組合以外，還可以通過ARIMA模型加外生變量來實現，那么這里要加的外生變量自然就是時間序列中的季節性序列了(通過時間序列分解得到)。需要注意的是，對於季節性來說，還是用季節性模型來擬合比較合適，這里用外生變量的方式只是為了方便演示外生變量的用法。因為對於引入了外生變量的時間序列模型來說，在預測未來的值的時候，也要對外生變量進行預測的，而用季節性做外生變量的方便演示之處在於，季節性每期都一樣的，比如年季節性，所以直接復制到3年就可以作為未來3年的季節外生變量序列了。

%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta
import seaborn as sns
import statsmodels.api as sm
from statsmodels.tsa.stattools import acf,pacf
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(df['riders'], freq=12)

def load_data():
    """
    航司乘客數時間序列數據集
    該數據集包含了1949-1960年每個月國際航班的乘客總數。
    """
    from datetime import datetime
    date_parse = lambda x: datetime.strptime(x, '%Y-%m-%d')
    data = pd.read_csv('https://www.analyticsvidhya.com/wp-content/uploads/2016/02/AirPassengers.csv', index_col='Month', parse_dates=['Month'], date_parser=date_parse)
    # print(data)
    # print(data.index)
    ts = data['value']
    # print(ts.head(10))
    # plt.plot(ts)
    # plt.show()
    return ts,data

# 加載時間序列數據
_ts,_data = load_data()
# 時間序列分解
result_mul = seasonal_decompose(_ts[-36:],  # 3 years
                                model='multiplicative',
                                freq=12,
                                extrapolate_trend='freq')
_seasonal_frame = result_mul.seasonal[-12:].to_frame()
_seasonal_frame['month'] = pd.to_datetime(_seasonal_frame.index).month
# seasonal_index = result_mul.seasonal[-12:].index
# seasonal_index['month'] = seasonal_index.month.values
print(_seasonal_frame)
_data['month'] = _data.index.month
print(_data)
_df = pd.merge(_data, _seasonal_frame, how='left', on='month')
_df.columns = ['value', 'month', 'seasonal_index']
print(_df)
print(_df.index)
_df.index = _data.index  # reassign the index.
print(_df.index)

build_arima(_df,_seasonal_frame,_data)

# SARIMAX Model
sxmodel = pm.auto_arima(df[['value']],
						exogenous=df[['seasonal_index']],
						start_p=1, start_q=1,
						test='adf',
						max_p=3, max_q=3, m=12,
						start_P=0, seasonal=False,
						d=1, D=1, trace=True,
						error_action='ignore',
						suppress_warnings=True,
						stepwise=True)
sxmodel.summary()
# Forecast
n_periods = 36
fitted, confint = sxmodel.predict(n_periods=n_periods,
								  exogenous=np.tile(seasonal_frame['y'].values, 3).reshape(-1, 1),
								  return_conf_int=True)
index_of_fc = pd.date_range(data.index[-1], periods = n_periods, freq='MS')
# make series for plotting purpose
fitted_series = pd.Series(fitted, index=index_of_fc)
lower_series = pd.Series(confint[:, 0], index=index_of_fc)
upper_series = pd.Series(confint[:, 1], index=index_of_fc)

# Plot
plt.plot(data['y'])
plt.plot(fitted_series, color='darkgreen')
plt.fill_between(lower_series.index,
				 lower_series,
				 upper_series,
				 color='k', alpha=.15)

plt.title("SARIMAX Forecast of a10 - Drug Sales")
plt.show()