【數據分析師 Level 1 】18.聚類分析

【數據分析師 Level 1 】18.聚類分析

層次聚類法

層次聚類法通常分為自底向上和自頂向下。兩種方法的運算原理其實是相同的。只不過實際計算是方向相反

自底向上，又叫做合並法。這種方法是先將每個樣本分別作為一個獨立的類，然后通過距離計算，將距離相近的兩個樣本合並為一類，其他樣本仍然各自為一類。不斷重復這個過程，直到達到聚類或者設定的目標。

而自頂向下的方法，剛好相反。這種方法先把所有樣本看成一類，然后通過距離計算，選出距離最遠的兩個樣本，各自為一個類別，其余樣本根據距離遠近分配到兩個類別中，從而形成新的類別划分。不斷重復過程，直到達到聚類數或者設定的目標，因此又叫做分解法。

不管是采用哪種層次聚類的方法，一個關鍵的問題就是距離的定義。

距離的計算

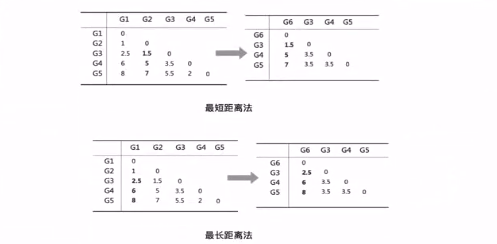
最短距離法

最短距離法（Neatest Neighbor）是指當我們從A中取出一個樣本，B中取出一個樣本，計算兩個樣本之間的距離，能夠得到的最小值就是A和B兩個類的距離。而最長距離法（Furthest Neighbor）則剛好相反。

中間距離法

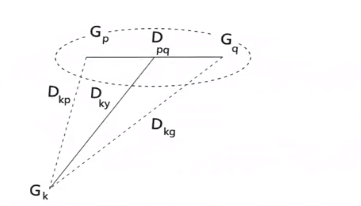
中間距離法是指最短距離法和最長距離法都是考慮的極端情況，因此也容易受到異常值的影響。我們可以采用一種折中的方式進行計算。加入類別A是由兩個小類別A1和A2合並而成的。那么類別A和類別B之間的距離，可以通過公式

\[D_{AB} = \sqrt{\frac{1}{2}D^2_{A_1B}+\frac{1}{2}D^2_{A_2B}-\frac{1}{4}D^2_{A_1A_2}} \]

來進行計算。它計算出來的長度在最短距離法和最長距離法結果之間，因此得名。

類平均法

類平均法（Between-groups-Linkage）是指把A中的點和B中的點進行連線，所有連線距離平方的平均值，就等於兩個類之間的距離平方。

可以用公式

\[D_{AB} = \sqrt{\frac{1}{n_An_B}\sum D^2_{ij}} \]

其中 i，j分別輸入類A和類B

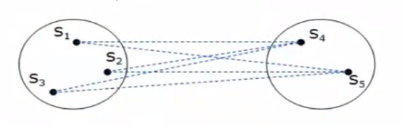
例如：

\[D^2_{12} = \frac{1}{6}(d^2_{14}+d^2_{15}+d^2_{24}+d^2_{25}+d^2_{34}+d^2_{35}) \]

重心法

重心法（Centroid Clustering）計算的是觀測類各自重心之間的距離。其實重心法和中間距離法是有些類似的，區別在於重心法是用

\[\frac{n_{A1}}{n_{A1}+n_{A2}} \]

和

\[\frac{n_{A2}}{n_{A1}+n_{A2}} \]

來代替原有的系數，所以公式也可以寫作：

\[\sqrt{\frac{n_{A1}}{n_{A1}+n_{A2}}D^2_{A_1B}+\frac{n_{A2}}{n_{A1}+n_{A2}}D^2_{A_2B}-\frac{n_{A_1}n_{A_2}}{n_{A_1}+n_{A_2}}D^2_{A_1A_2}} \]

\[D_{centroids}(C_i,C_j) = d(r_i,r_j) \]

其中r表示重心

離差平方和法

離差平方和法，又叫Ward最小方差法（Ward‘s Method）：這種方法主要基於方差分析的思想，如果分類合理，則同類樣本間離差平方和應當較小，類與類間離差平方和應當較大。每次合並類別時，離差平方和會增大，選擇使得增加值最小的兩類進行合並。因此，該方法很少受到異常值的影響，在實際應用中的分類效果較好，使用范圍廣。但該方法要求樣品間的距離必須是歐式距離

層次聚類的過程非常清楚，會形成類似樹狀的聚類圖譜，便於理解和檢查。聚類的變量可以是連續變量，也可以是分類變量。衡量距離的方法也非常反復。

但是由於需要反復計算距離，限制了層次聚類的速度。因此不適用於數量非常大或者變量非常多的項目。如果計算機的硬件有制約，也會影響層次聚類的可行性。

快速聚類-Kmeans聚類

不同於層次聚類，K-Means聚類是一種快速聚類法，因此也適合應用於大樣本量的數據，或者是進行一些前期的數據清洗工作。K-Means聚類方法需要分析師自行指定聚類的數量，也就是其中的K。因此在實際分析過程中，往往需要多次調整K的取值，反復嘗試，以便獲得最優的聚類結果。

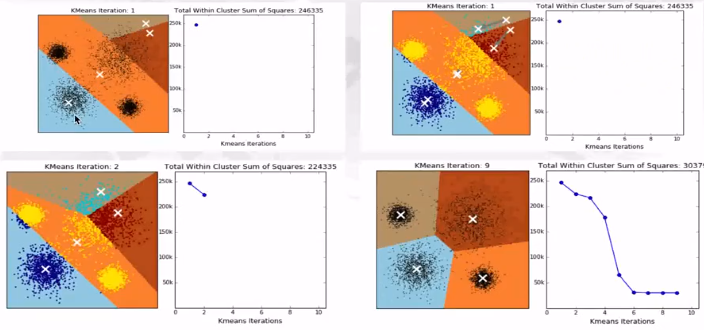
其方法可以總結為：首先選擇K個點作為中心點，這些中心點可以是分析者自己指定的，也可以是數據本身結構形成的。或者是隨機產生。所有樣本與這K個中心點計算距離，按照距離最近的原則歸入這些中心點，然后重新計算每個類的中心，再次計算每個樣本與類中心的距離，並按照最短距離原則重新划分類，如此迭代直至類不再變化為止。

和層次聚類法相比，快速聚類法計算量非常小，即便在樣本數據量較大或者變量較多的情況下，仍然可以快速得出結果，不會耗費太多的空間和時間，對硬件的依賴性也較低。它因此得名快速聚類法。在分析時，用戶也可以根據過往經驗或計算結果，指定初始中心點位置，也可以進一步增加聚類的效率。

但是這個方法應用范圍也比較有限，因為需要事先指定聚類數，因此需要分析師有一定的經驗積累，或者可能需要多次反復嘗試。對初始點位置也很敏感，容易導致聚類結果與數據真實分類出現差異，對異常值也比較敏感。同時聚類的變量也必須是連續變量，對變量的“標准度”要求也相對較高，否則可能產生無意義的結果。而且K-Means聚類方法並不能對變量進行聚類，也是它使用上的一個比較大的缺點。

兩步聚類法

兩步聚類法結合了K-Means和系統聚類法，先選擇較大的類數量對於樣本進行快速聚類，然后對每個聚類的中心點進行系統聚類，選擇合適的分類數量，然后將聚類結果合並為較理想的數量

在進行聚類時，要結合業務理解對數據進行適當變換，並且需要對變量進行維度分析，聚類結果可以使用類中心之間的比較，結合業務進行解讀。

聚類的實際應用

在實際使用聚類方法時，我們一般多用於客戶畫像、離群點檢驗、營銷套餐設計等領域，我們需要注意選取合適的聚類方法。對於數據量較大或變量較多的樣本，優先考慮K-Means聚類法。樣本數據量適中或者變量類型比較復雜的情況，則可以考慮使用層次聚類法。特別綜合的項目，也可以采用兩步聚類法，結合兩種聚類方法各自的優勢，高效解決問題。

再聚類之前，數據清洗也是非常重要的。標准化可以幫助我們消除不同變量之間的量綱的差異，但是需要注意的是，在有些場景，比如欺詐分析時，我們希望通過聚類去發現異常值，那么前期的數據清洗就要注意不能改變原有的分布情況，避免造成結果偏差。因此分箱法、小數定標法等清洗方法在聚類問題中需要謹慎使用。另外，通過主成分分析或者因子分析等方法對變量進行降維，或者先進行變量聚類，也可以幫助減少冗余變量，更有效地完成聚類。

在一些場景下，直接的業務字段並不能很好的進行量化和數學分析，那么我們需要通過函數或者其他的方式，將其進行轉換，靈活應用才能更好地解決問題。

聚類本身是一種數據算法，聚類的結果並不是總是有實際的使用意義。因此對於聚類結果，我們需要謹慎地解讀，適當地對其進行修正和調整，從而更加貼近業務的使用。

最后，需要注意的是，聚類是一種無監督學習的算法，因此也並沒有統一的評判標准。因此在實際使用過程中，我們可以把聚類結果和認為選擇或隨機選擇的結果放在一起進行比較，這個時候，我們可以通過觀察聚類是否對整體的分類或者研究有提升作用來評判聚類的好壞。

當然，我們一般也可以近似地用組間平方和BSS(Between Sum of Squares)和組內平方和WSS(Within Sum of Squares)來作為評價指標判斷聚類的類別數是否合適。顯然BSS越大，WSS越小，聚類的效果就越好。

另外，只有兩個變量的時候，我們也可以通過畫圖的方法來進行觀察和評估。

例題精講

1.以下哪種聚類方法可以提供聚類樹形圖（）？

A.層次聚類

B.K均值聚類

C.基於密度的聚類

D.基於網格的聚類

答案：A

解析：層次聚類指的是形成類相似度層次圖譜，便於直觀地確定類之間的划分，聚類過程可做成聚類譜系圖。聚類譜系圖的基本思路就在於按照兩點之間的距離，按照由小到大的順序依次進行連接。

2.以下哪個是K均值聚類法的缺陷（）？

A.對初始點位置敏感，導致聚類結果與數據真實分類出現差異

B.無法通過分析方法確定聚類個數

C.容易受到異常值的影響

D.容易受到變量量綱的影響

答案：ABC

解析：這部分試題主要考核層次聚類和K均值快速聚類的優缺點和適用范圍。當樣本量超過50個時，一般采用K均值聚類法，其優點是計算速度快，但是缺點是ABC答案列出的那樣。

3.某電商分析人員希望通過聚類方法定位代商家刷信用級別的違規者，以下哪些操作不應該進行？

A.對變量進行標准化

B.對變量進行百分位秩轉換

C.對變量進行因子分析或變量聚類

D.對變量進行分箱處理

答案：BD

解析：刷信用級別的違規者的行為會與正常消費行為在消費頻次、平均消費金額等方面差異比較大，對其進行定位相當於發現異常點，因此要求對變量的轉換不能改變其原有分布形態。常用的標准化方法如中心標准化、極差標准化不會改變分布形態，而且在聚類前往往需要使用標准化來消除變量的量綱，因此A不是答案；取百分位秩會將原變量變化為均勻分布，進行分箱處理也會改變原變量的分布，因此BD是答案；因子分析、變量聚類用於數據降維，可以使聚類結果更合理。