DDPG原理和算法
以下用RL作為Reinforcement Learning的簡稱。
背景描述
概括來說，RL要解決的問題是：讓agent學習在一個環境中的如何行為動作(act)， 從而獲得最大的獎勵值總和(total reward)。
這個獎勵值一般與agent定義的任務目標關聯。
agent需要的主要學習內容：第一是行為策略(action policy)， 第二是規划(planning)。
其中，行為策略的學習目標是最優策略， 也就是使用這樣的策略， 可以讓agent在特定環境中的行為獲得最大的獎勵值，從而實現其任務目標。
行為(action)可以簡單分為：
-
連續的：如賽車游戲中的方向盤角度、油門、剎車控制信號，機器人的關節伺服電機控制信號。
-
離散的：如圍棋、貪吃蛇游戲。 Alpha Go就是一個典型的離散行為agent。
DDPG是針對連續行為的策略學習方法。
如果要了解完整和系統的RL背景知識，推薦大家看R.Sutton的這本書： 《Reinforcement Learning: An Introduction, by Sutton, R.S. and Barto, A.G.》
DDPG的定義和應用場景
在RL領域，DDPG主要從：PG -> DPG -> DDPG發展而來。
先復述一下相關的基本概念：
-
：在t時刻，agent觀察到的環境狀態，比如觀察到的環境圖像，agent在環境中的位置、速度、機器人關節角度等； -
：在t時刻，agent選擇的行為（action），通過環境執行后，環境狀態由
轉換為
； -
函數：環境在狀態
執行行為
后，返回的單步獎勵值；上述關系可以用一個狀態轉換圖來表示：
-
：是從當前狀態直到將來某個狀態，期間所有行為所獲得獎勵值的加權總和，即discounted future reward:
其中γ叫做discounted rate, ∈[0,1] ,通常取0.99.
PG
R.Sutton 在2000年提出的Policy Gradient方法，是RL中，學習連續的行為控制策略的經典方法，其提出的解決方案是： 通過一個概率分布函數 
， 來表示每一步的最優策略， 在每一步根據該概率分布進行action采樣，獲得當前的最佳action取值；即：
生成action的過程，本質上是一個隨機過程；最后學習到的策略，也是一個隨機策略(stochastic policy).
DPG
Deepmind的D.Silver等在2014年提出DPG： Deterministic Policy Gradient， 即確定性的行為策略，每一步的行為通過函數
直接獲得確定的值：
這個函數
即最優行為策略，不再是一個需要采樣的隨機策略。
為何需要確定性的策略？簡單來說，PG方法有以下缺陷：
-
即使通過PG學習得到了隨機策略之后，在每一步行為時，我們還需要對得到的最優策略概率分布進行采樣，才能獲得action的具體值；而action通常是高維的向量，比如25維、50維，在高維的action空間的頻繁采樣，無疑是很耗費計算能力的；
-
在PG的學習過程中，每一步計算policy gradient都需要在整個action space進行積分:
(
,
參見下面DDPG部分的概念定義.)
這個積分我們一般通過Monte Carlo 采樣來進行估算，需要在高維的action空間進行采樣，耗費計算能力。如果采取簡單的Greedy策略，即每一步求解
也不可行，因為在連續的、高維度的action空間，如果每一步都求全局最優解，太耗費計算性能。在這之前，業界普遍認為，環境模型無關(model-free)的確定性策略是不存在的，在2014年的DPG論文中，D.Silver等通過嚴密的數學推導，證明了DPG的存在， 其數學表示參見DDPG算法部分給出的公式 (3)。
然后將DPG算法融合進actor-critic框架，結合Q-learning或者Gradient Q-learning這些傳統的Q函數學習方法，經過訓練得到一個確定性的最優行為策略函數。
DDPG
Deepmind在2016年提出DDPG，全稱是：Deep Deterministic Policy Gradient,是將深度學習神經網絡融合進DPG的策略學習方法。
相對於DPG的核心改進是： 采用卷積神經網絡作為策略函數μμ和QQ函數的模擬，即策略網絡和Q網絡；然后使用深度學習的方法來訓練上述神經網絡。
Q函數的實現和訓練方法，采用了Deepmind 2015年發表的DQN方法 ,即 Alpha Go使用的Q函數方法。
DDPG算法相關基本概念定義
我們以Open Gym 作為環境為例來講解。
先復述一下DDPG相關的概念定義：
-
確定性行為策略
: 定義為一個函數，每一步的行為可以通過 
計算獲得。 -
策略網絡：用一個卷積神經網絡對
函數進行模擬，這個網絡我們就叫做策略網絡，其參數為
; -
behavior policy
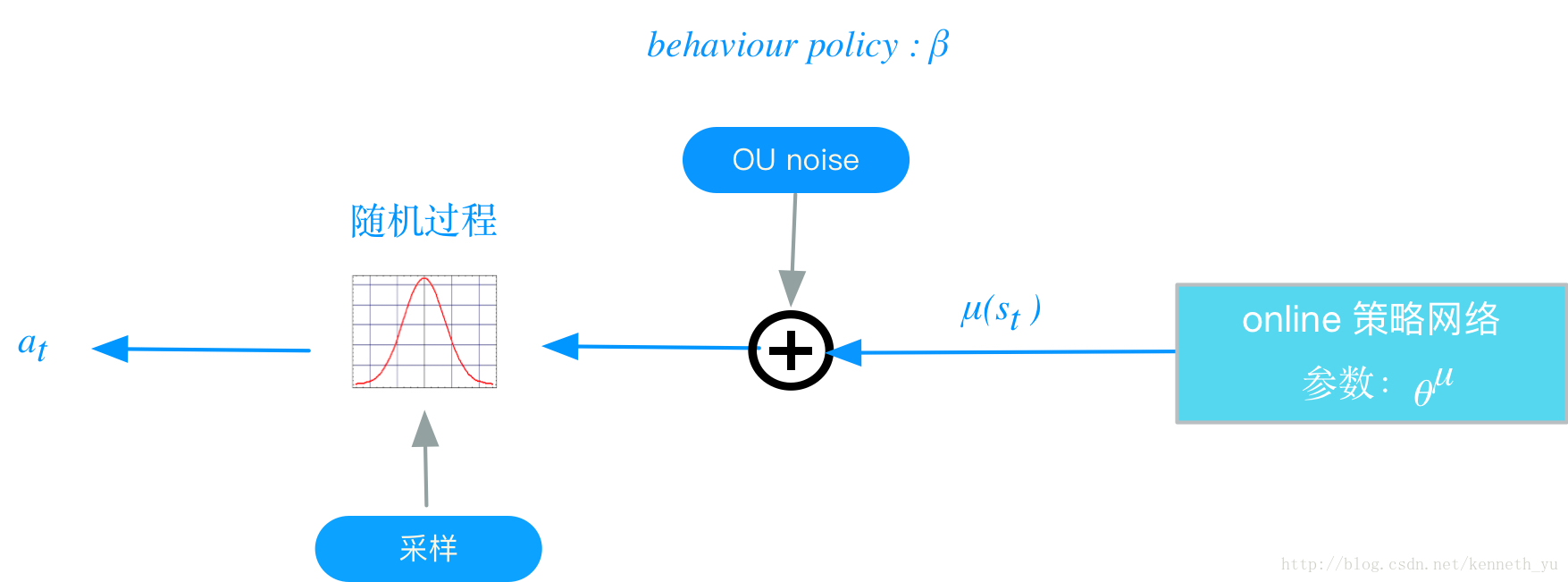
: 在RL訓練過程中，我們要兼顧2個e: exploration和exploit；exploration的目的是探索潛在的更優策略，所以訓練過程中，我們為action的決策機制引入隨機噪聲：將action的決策從確定性過程變為一個隨機過程， 再從這個隨機過程中采樣得到action，下達給環境執行.
過程如下圖所示：
上述這個策略叫做behavior策略，用
來表示, 這時RL的訓練方式叫做off-policy.這里與ϵ−greedy的思路是類似的。
DDPG中，使用Uhlenbeck-Ornstein隨機過程（下面簡稱UO過程），作為引入的隨機噪聲： UO過程在時序上具備很好的相關性，可以使agent很好的探索具備動量屬性的環境。
注意：
– 這個
不是我們想要得到的最優策略，僅僅在訓練過程中，生成下達給環境的action， 從而獲得我們想要的數據集，比如狀態轉換(transitions)、或者agent的行走路徑等，然后利用這個數據集去 訓練策略
，以獲得最優策略。
– 在test 和 evaluation時，使用
，不會再使用
。 -
函數: 即action-value 函數，定義在狀態
下，采取動作
后，且如果持續執行策略
的情況下， 所獲得的 
期望值, 用Bellman 等式來定義：
可以看到，
函數的定義是一個遞歸表達，在實際情況中，我們不可能每一步都遞歸計算Q的值， 可行的方案是通過一個函數對Bellman等式表達進行模擬。 -
網絡：DDPG中，我們用一個卷積神經網絡對
函數進行模擬，這個網絡我們就叫做
網絡， 其參數為
。采用了DQN相同的方法。 -
如何衡量一個策略
的表現：用一個函數
來衡量，我們叫做performance objective，針對off-policy學習的場景，定義如下：
其中：
-
是環境的狀態，這些狀態(或者說agent在環境中走過的狀態路徑)是基於agent的behavior策略產生的，它們的分布函數(pdf) 為
； -
是在每個狀態下，如果都按照
策略選擇acton時，能夠產生的Q值。
也即，
是在
根據
分布時，
的期望值。 -
訓練的目標： 最大化
，同時最小化
網絡的Loss(下面描述算法步驟時會給出)。 -
最優行為策略
的定義: 即最大化
的策略：
訓練
網絡的過程，就是尋找
網絡參數
的最優解的過程， 我們使用SGA(stochastic gradient ascent)的方法。
-
最優
網絡定義：具備最小化的
網絡Loss；訓練
網絡的過程，就是尋找
網絡參數
的最優解的過程，我們使用SGD的方法。
DDPG實現框架和算法
online 和 target 網絡
以往的實踐證明，如果只使用單個”Q神經網絡”的算法，學習過程很不穩定，因為Q網絡的參數在頻繁gradient update的同時，又用於計算Q網絡和策略網絡的gradient, 參見下面等式(8),(9),(10).
基於此，DDPG分別為策略網絡(8)、Q網絡(9)各創建兩個神經網絡拷貝，一個叫做online，一個叫做target：
在訓練完一個mini-batch的數據之后，通過SGA/SGD算法更新online網絡的參數，然后再通過soft update算法更新 target 網絡的參數。soft update是一種running average的算法：
- 優點：target網絡參數變化小，用於在訓練過程中計算online網絡的gradient，比較穩定，訓練易於收斂。
- 代價：參數變化小，學習過程變慢。
DDPG實現框架，如下圖所示：
DDPG算法流程如下：
初始化actor\critic的 online 神經網絡參數:
和
；
將online網絡的參數拷貝給對應的target網絡參數：
,
;
初始化replay memory buffer
;
for each episode:
初始化UO隨機過程；
for t = 1, T:
下面的步驟與DDPG實現框架圖中步驟編號對應：
actor 根據behavior策略選擇一個
, 下達給gym執行該
;
behavior策略是一個根據當前online策略和隨機UO噪聲生成的隨機過程, 從這個隨機過程采樣 獲得
的值。
gym執行
，返回reward
和新的狀態
;
actor將這個狀態轉換過程(transition):
存入replay memory buffer
中，作為訓練online網絡的數據集。
從replay memory buffer
中，隨機采樣
個 transition 數據，作為online策略網絡、 online Q網絡的一個mini-batch訓練數據。我們用表示
mini-batch中的單個transition數據。
計算online Q網絡的 gradient：
網絡的loss定義：使用類似於監督式學習的方法，定義loss為MSE: mean squared error：
其中，可以看作“標簽”：
基於標准的back-propagation方法，就可以求得針對
的gradient：
。
有兩點值得注意：
的計算，使用的是 target 策略網絡
和 target Q 網絡
, 這樣做是為了Q網絡參數的學習過程更加穩定，易於收斂。
- 這個標簽本身依賴於我們正在學習的target網絡，這是區別於監督式學習的地方。
update online Q： 采用Adam optimizer更新
;
計算策略網絡的policy gradient：
policy gradient的定義：表示performance objective的函數針對
的 gradient。 根據2015 D.Silver 的DPG 論文中的數學推導，在采用off-policy的訓練方法時，policy gradient算法如下：
也即，policy gradient是在根據
分布時，
的期望值。 我們用Monte-carlo方法來估算這個期望值：
在replay memory buffer中存儲的(transition):, 是基於agent的behavior策略
產生的，它們的分布函數(pdf)為
，所以當我們從replay memory buffer中隨機采樣獲得mini-batch數據時，根據Monte-carlo方法，使用mini-batch數據代入上述policy gradient公式，可以作為對上述期望值的一個無偏差估計 (un-biased estimate), 所以policy gradient 可以改寫為：
update online策略網絡：采用Adam optimizer更新
;
soft update target網絡
和 :
使用running average 的方法，將online網絡的參數，soft update給target網絡的參數：
end for time step
end for episode
總結一下：
actor-critic框架是一個在循環的episode和時間步驟條件下，通過環境、actor和critic三者交互，來迭代訓練策略網絡、Q網絡的過程。
DDPG對於DPG的關鍵改進
-
使用卷積神經網絡來模擬策略函數和Q函數，並用深度學習的方法來訓練，證明了在RL方法中，非線性模擬函數的准確性和高性能、可收斂；
而DPG中，可以看成使用線性回歸的機器學習方法：使用帶參數的線性函數來模擬策略函數和Q函數，然后使用線性回歸的方法進行訓練。
-
experience replay memory的使用：actor同環境交互時，產生的transition數據序列是在時間上高度關聯(correlated)的，如果這些數據序列直接用於訓練，會導致神經網絡的overfit，不易收斂。
DDPG的actor將transition數據先存入experience replay buffer, 然后在訓練時，從experience replay buffer中隨機采樣mini-batch數據，這樣采樣得到的數據可以認為是無關聯的。 -
target 網絡和online 網絡的使用， 使的學習過程更加穩定，收斂更有保障。