【論文筆記系列】自動搜索損失函數？AM-LFS：AutoML for Loss Function Search

目前AutoML技術非常火，尤其是NAS領域，之前有一篇文章已經對現有的AutoML技術做了總結，可閱讀【AutoML：Survey of the State-of-the-Art】。

論文：AM-LFS：AutoML for Loss Function Search

不過這篇文章將介紹一下如何使用AutoML技術來搜索損失函數。一般來說，損失函數都是需要我們手動設計的，以分類任務而言，我們通常會使用交叉熵。碰到數據集imbalanced的情況，可能會給每個類別加上一個權重。在RetinaNet論文里為目標檢測任務提出了FocalLoss。上述都是對交叉熵函數根據特定任務做了修改，可是這樣的修改通常需要我們能夠洞察到問題的本質，換句話說這需要專業的知識。那我們這種蔡文姬還有設計loss函數的機會嗎？商湯科技在這方面做了探索，下面將介紹論論文細節。

1. 論文貢獻

論文有兩大貢獻：

• 設計了損失函數搜索空間，該搜索空間能夠覆蓋常用的流行的損失函數設計，其采樣的候選損失函數可以調整不同難度級別樣本的梯度，並在訓練過程中平衡類內距離和類間距離的重要性。
• 提出了一個bilevel的優化框架：本文使用強化學習來優化損失函數，其中內層優化是最小化網絡參數的損失函數，外層優化是最大化reward。

2. 回顧之前的損失函數

• Softmax Loss

\[L=\frac{1}{N} \sum_{i} L_{i}=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{f_{y_{i}}}}{\sum_{j} e^{f_{j}}}\right) \tag{1} \]

\(N\)表示數據集大小，\(f\)是最后全連接層輸出的預測向量（還沒有做softmax運算），\(f_j\)表示向量\(f\)的第\(j\)位置上的值，因為真實值是one-hot的向量（即只有一個1，其余全是0），\(f_{y_i}\)中的\(y_i\)表示1的索引值。

因為\(f\)是最后全連接層的輸出，所以我們可以將它表示成

\[f_{j}=\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right) \tag{2} \]

其中\(\theta_{j}\left(0 \leq \theta_{j} \leq \pi\right)\)是矢量\(\|\boldsymbol{W}_{j}\|\)和\(x_i\)之間的夾角，所以上面公式(1)中的損失函數可以轉換成

\[L_{i}=-\log \left(\frac{e^{ \| \boldsymbol{W}_{y_{i}}\| \| \boldsymbol{x}_{i} \| \cos \left(\theta_{y_{i}}\right)}}{\sum_{j} e^{\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right)}}\right) \tag{3} \]

• Margin-based Softmax Loss

看到公式(3)可以很自然地想到能在\(\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\|\) 和 \(\cos \left(\theta_{y_{i}}\right)\)之間能夠插入一個可微變換函數\(t( \cdot )\)來調節角度，進而得到margin可變的softmax loss：

\[L_{i}^{t}=-\log \left(\frac{e^{\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| t\left(\cos \left(\theta_{y_{i}}\right)\right)}}{e^{\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| t\left(\cos \left(\theta_{y_{i}}\right)\right)}+\sum_{j \neq y_{i}} e^{\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right)}}\right)\tag{4} \]

不同的\(t(\cdot)\)可以得到不同的損失函數，原文中總結了如下幾種：

• Focal Loss

除了在概率上做變化外，Focal Loss對softmax loss做了如下變化：

\[\begin{array}{l} L_{i}^{t}=-\tau\left(\log \left(p_{y_{i}}\right)\right) \\ \tau(x)=x\left(1-e^{x}\right)^{\alpha} \tag{5} \end{array}\]

3. Loss函數分析

3.1 Focal Loss

focal loss的提出主要是為了解決imbalanced的問題。相對於原始的softmax loss，focal loss在求導之后等於原始的softmax loss求導結果再乘以\(\tau^{\prime}\left(\log \left(p_{y_{i}}\right)\right.\)，換言之\(\tau^{\prime}\)用來緩解imbalance的問題。

3.2 margin-based softmax loss

為方便說明，我們可以假設所有的矢量是單位矢量，即\(\left\|\boldsymbol{W}_{j}\right\|=\left\|\boldsymbol{x}_{i}\right\|=1\) 和 \(f_{j}=\cos \left(\theta_{j}\right)\)

我們使用公式(4)中的損失函數來分別對\(f_{y_i}\)（類內，intra-class）和\(f_j\)（類間，inter-class）求導，得到：

\[\left\|\frac{\partial L_{i}^{t}}{\partial f_{y_{i}}}\right\|=\left(1-p_{y_{i}}^{t}\right) t^{\prime}\left(f_{y_{i}}\right) \tag{6} \]

\[\left\|\frac{\partial L_{i}^{t}}{\partial f_{j}}\right\|=p_{j}^{t} \tag{7} \]

其中

\[p_{y_{i}}^{t}=\frac{e^{\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| t\left(\cos \left(\theta_{y_{i}}\right)\right)}}{e\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| t\left(\cos \left(\theta_{y_{i}}\right)\right)+\sum_{j \neq y_{i}} e^{\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right)}} \]

\[p_{j}^{t}=\frac{e^{\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right)}}{e\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| t\left(\cos \left(\theta_{y_{i}}\right)\right)+\sum_{j \neq y_{i}} e^{\left\|W_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right)}} \]

文中進一步將類內距離與類間距離的相對重要性定義為\(f_{y_i}\)和\(f_j\)的梯度范數相對於margin-based softmax loss的比率 （\(r_{i}^{t}\)中的\(t\)就是表示前面提到的t函數）:

\[r_{i}^{t}=\frac{\left\|\frac{\partial L_{i}^{t}}{\partial f_{y_{i}}}\right\|}{\left\|\frac{\partial L_{i}^{t}}{\partial f_{j}}\right\|}=\frac{\left(1-p_{y_{i}}^{t}\right)}{p_{j}^{t}} t^{\prime}\left(f_{y_{i}}\right) \tag{8} \]

同理相對於原始的softmax loss（公式1）的重要性比率是：

\[r_{i}^{o}=\frac{\left\|\frac{\partial L_{i}^{o}}{\partial f_{y_{i}}}\right\|}{\left\|\frac{\partial L_{i}^{o}}{\partial f_{j}}\right\|}=\frac{\left(1-p_{y_{i}}^{o}\right)}{p_{j}^{o}}\tag{9} \]

進一步可以求得：

\[\begin{array} \frac{r_{i}^{t}}{r_{i}^{o}}&=\frac{\frac{\left(1-p_{y_{i}}^{t}\right)}{p_{j}^{t}}}{\frac{\left(1-p_{y_{i}}^{o}\right)}{p_{j}^{o}}} t^{\prime}\left(f_{y_{i}}\right) = \frac{ \frac{\sum_{t \neq y_{i}} e^{\left\|\boldsymbol{W}_{t}\right\|\left\|x_{i}\right\| \cos \left(\theta_{t}\right)}}{e^{\left\|\boldsymbol{W}_{j}\right\|\left\|x_{i}\right\| \cos \left(\theta_{j}\right)}}}{\frac{\sum_{t \neq y_{i}} e^{\left\|W_{t}\right\|\left\|x_{i}\right\| \cos \left(\theta_{t}\right)}}{e^{\left\|W_{j}\right\|\left\|x_{i}\right\| \cos \left(\theta_{j}\right)}}}t^{\prime}\left(f_{y_{i}}\right)\\ &=t^{\prime}\left(f_{y_{i}}\right) \tag{10} \end{array} \]

由公式10可以知道定義的損失函數表達式（公式4）中的\(t(\cdot)\)的導函數實際上是具有控制類內距離對於類間距離顯著性的作用

4. 搜索空間

基於第3節的分析，我們可以知道可以在公式（3）作如下兩處的變換：

\[L_{i}^{\tau, t}=-\tau\left(\log \left(p_{y_{i}}^{t}\right)\right) \tag{11} \]

其中\(\tau\)和\(t\)是需要我們進行搜索的任意函數。另外上式中的\(\tau\)的定義域在\([-\infty，0]\)，為了使得其定義域在\([0,1]\)進而簡化搜索空間，將公式(11)作如下變化 （令公式(12)中的\(\tau_{2}(x)=e^{\tau_{1}(\log (x))}\)可以使得公式(11)和公式(12)等價）：

\[L_{i}^{\tau, t}=-\log \left(\tau\left(p_{y_{i}}^{t}\right)\right) \tag{12} \]

其中（注意看清楚\(t\)和\(\tau\)）

• \(t(\cdot)=a_{i}^{t} x+b_{i}^{t}, x \in\left[\zeta_{i}^{t}, \zeta_{i+1}^{t}\right]\)
  • \(\zeta^{t}=\left[\zeta_{0}, \ldots \zeta_{M}\right]\)
  • \(M\)表示間隔數，即\(\zeta_{i+1}^{t}-\zeta_{i}^{t}=\left(\zeta_{M}^{t}-\zeta_{0}^{t}\right) / M\)
  • 所以\(t(\cdot)\)函數由三個超參數組成\(a_{i}^{t}, b_{i}^{t}\) and \(\zeta_{i}^{t}\)
• \(\tau\)同理由三個超參數組成：\(a_{i}^{\tau}, b_{i}^{\tau}\) and \(\zeta_{i}^{\tau}\)

另外\(\zeta_{i}^{t}\)和\(\zeta_{i}^{\tau}\)需要實現設定好，那么最后搜索空間定義為

\[\boldsymbol{\theta}=\left[\boldsymbol{a}^{t^{T}}, \boldsymbol{b}^{t^{T}}, \boldsymbol{a}^{\tau T}, \boldsymbol{b}^{\tau T}\right]^{T} \tag{13} \]

5. 優化

雙層（Bilevel）優化定義如下：

\[\begin{array}{l} \max _{\boldsymbol{\theta}} R(\boldsymbol{\theta})=r\left(M_{\boldsymbol{\omega}^{*}}(\boldsymbol{\theta}), \mathcal{D}_{v}\right) \\ \text { s.t. } \boldsymbol{\omega}^{*}(\boldsymbol{\theta})=\arg \min _{\boldsymbol{\omega}} \sum_{(x, y) \in \mathcal{D}_{t}} L^{\boldsymbol{\theta}}\left(M_{\boldsymbol{\omega}}(x), y\right) \tag{14} \end{array}\]

可以看到

• 內層優化是在固定損失函數后，在訓練集上更新模型超參數使得損失函數值最小，得到當前最優的模型參數\(\omega^*(\theta)\)
• 外層優化則是去找到一組損失函數搜索空間超參數\(\theta\)使得最優的模型參數\(\omega^*(\theta)\)在驗證集上能取得最大的獎勵。

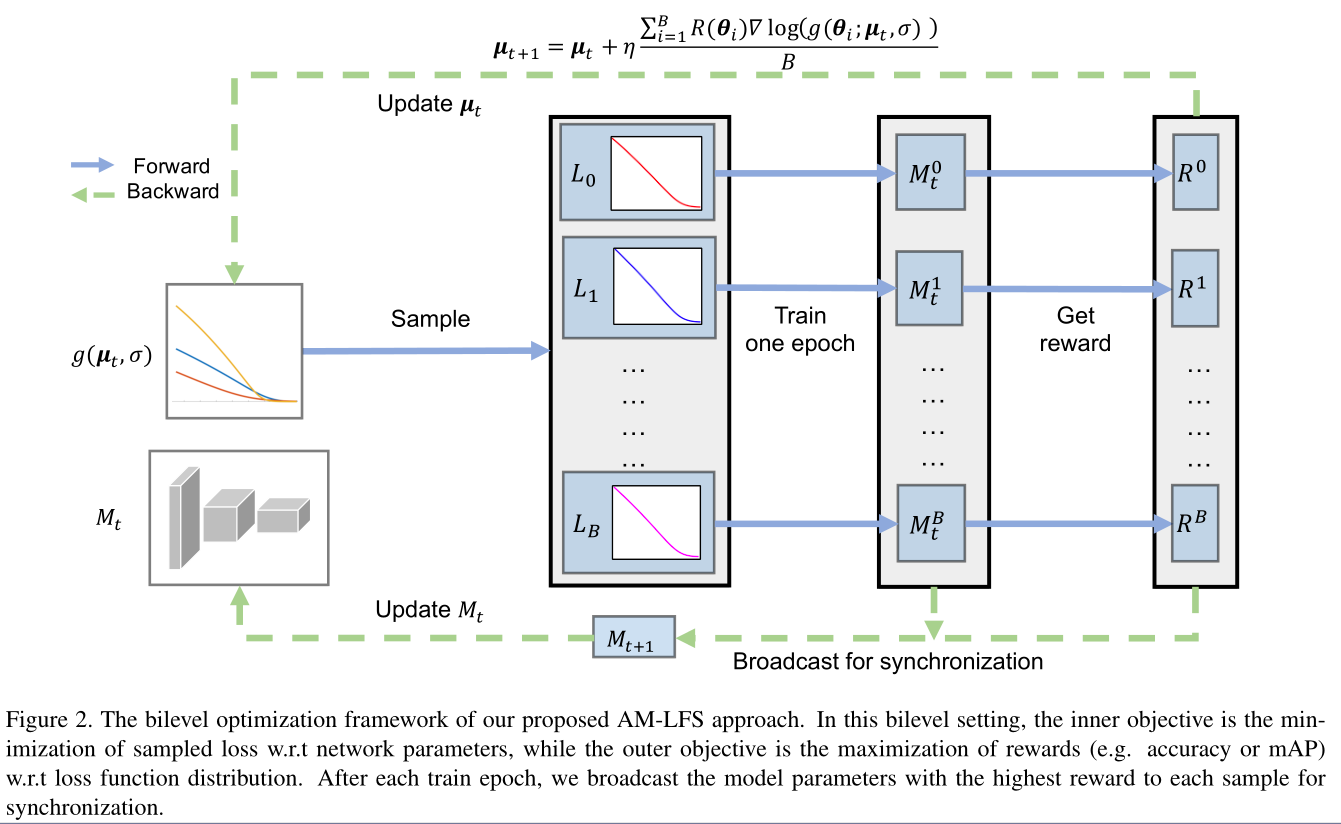
內層優化比較好理解，可是外層優化應該是固定的模型參數，那么最后無論損失函數是什么都不會影響模型輸出吧，那怎么最大化獎勵呢？文中的做法是這樣的（可結合下面的算法流程圖來理解）：

1. 在每個epoch采樣\(B\)組損失函數超參數\(\left\{\boldsymbol{\theta}_{1}, \ldots \boldsymbol{\theta}_{B}\right\}\)，其中超參數\(\theta\)服從獨立的高斯分布，即\(\boldsymbol{\theta} \sim \mathcal{N}(\boldsymbol{\mu}, \sigma I)\)。
2. 先后用\(B\)個損失函數來訓練當前的模型，得到\(\{M_t^0,...,M_t^B\}\)，計算每個模型在驗證集上的reward，即\(\{R^0,...,R^B\}\)。
3. 更新：
   • 更新模型權重\(\omega\)：選擇reward最大的模型權重作為下一個epoch模型
   • 更新搜索空間\(\theta\)：\(\mu_{t+1}=\mu_{t}+\eta \frac{1}{B} \sum_{i=1}^{B} R\left(\theta_{i}\right) \nabla_{\theta} \log \left(g\left(\theta_{i} ; \mu_{t}, \sigma\right)\right)\)，其中\(g(\boldsymbol{\theta} ; \boldsymbol{\mu}, \sigma)\)是高斯分布的PDF（概率密度函數），為了簡化難度，方差\(\sigma\)是固定的，因此只需要更新均值\(\mu\)。

6. 實驗結果

原論文給出了在多個不同類型的數據集的結果：

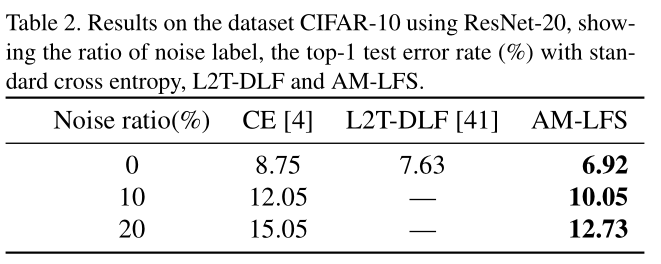
• Classification: Cifar10

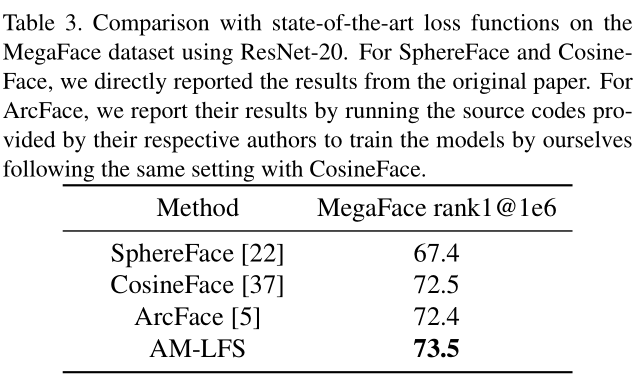
• Face Recognition：CASIA-Webface用作訓練集，MegaFace用做測試集

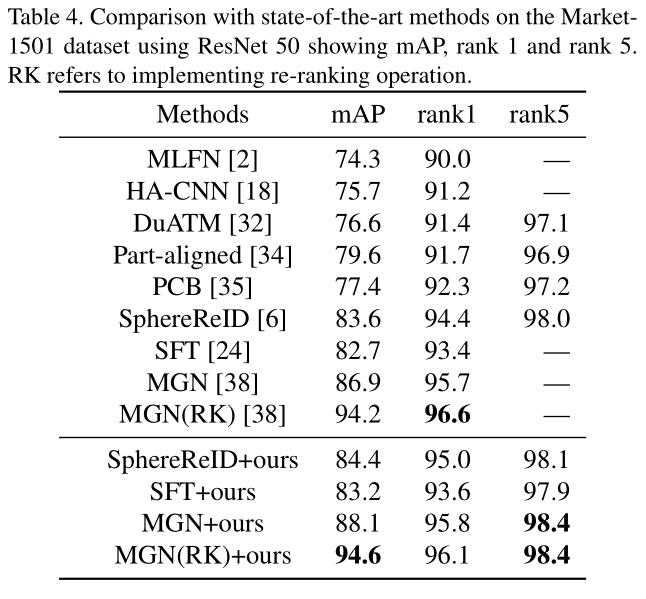
• Person ReID：Market-1501 and DukeMTMC-reID

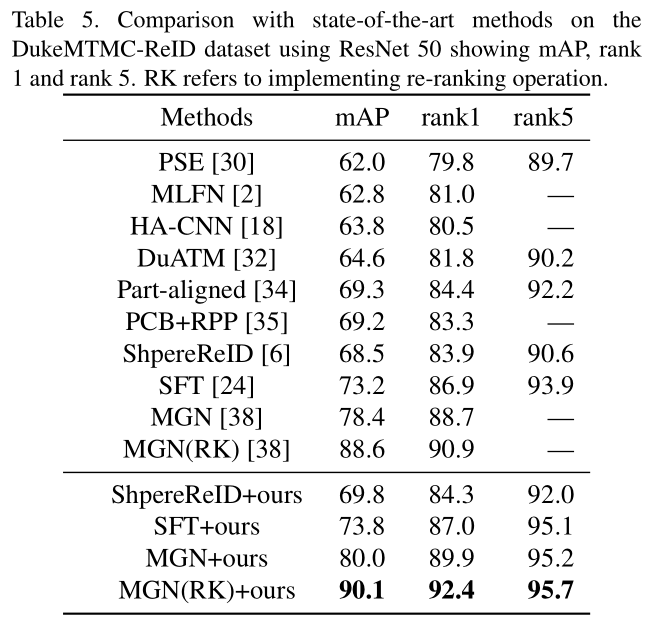7. 討論

本小節是我自己在讀完這篇論文后的一些存疑或者覺得需要討論的點：

• 文中搜索空間的構造引入了兩個需要手動設計的超參數（公式12和13），即\(\zeta_{i}^{t}\)和\(\zeta_{i}^{\tau}\)，這或多或少依賴於手動調參技巧。
• 文中的損失函數搜索只是局限在了對softmax loss函數的變體搜索，而且對於多loss組成的任務，論文僅僅對softmax loss部分做了替換，其余部分保持不變。
• 由算法流程圖可以看到，每個epoch都需要基於多個損失函數來訓練模型，然后再在驗證集上得到reward，這需要大量的計算資源，論文中說了，他們使用了64個GPU，這個emm。。。大力出奇跡，贊！

本篇文章是基於自己的理解寫的，所以可能會有不正確的地方，歡迎指正！

微信公眾號：AutoML機器學習
MARSGGBO♥原創
如有意合作或學術討論歡迎私戳聯系~
郵箱:[e-mail]
2020-08-11 17:30:58