一、簡單回顧DARTS
在介紹gumbel softmax之前,我們需要首先介紹一下什么是可微NAS。
可微NAS(Differentiable Neural Architecture Search, DNAS)是指以可微的方式搜索網絡結構,比較經典的算法是DARTS,其算法示意圖如下:
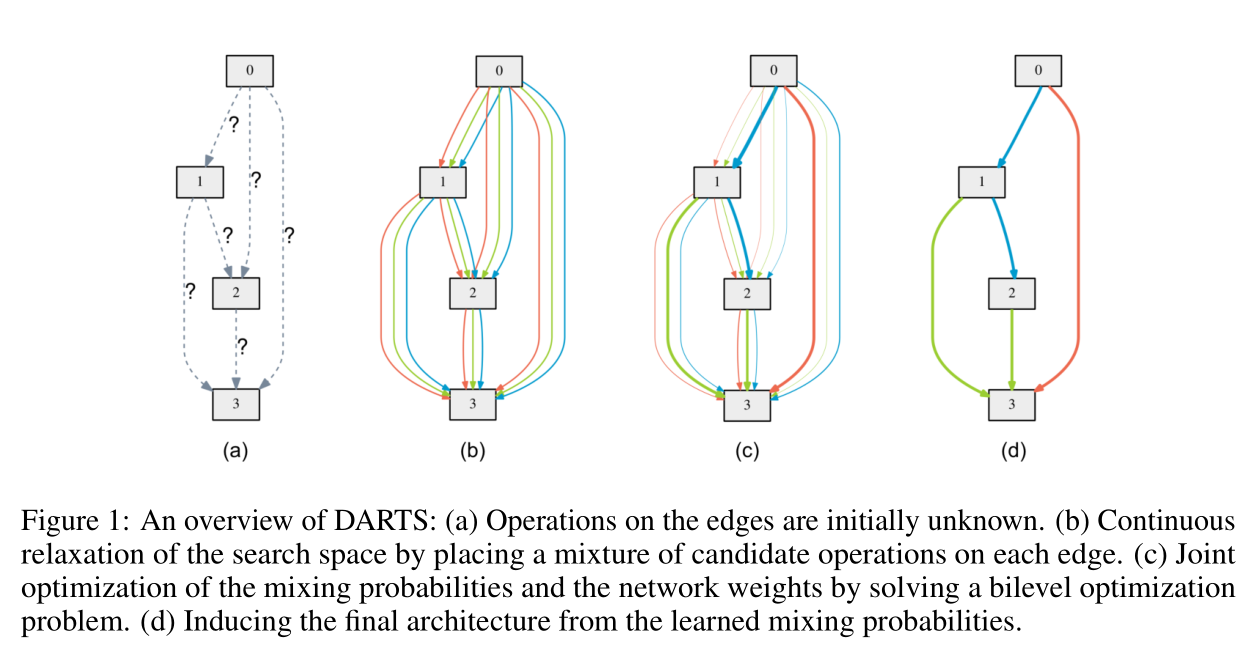
上圖表示的是一個cell的結構。一個cell由若干個節點(node)組成,每組節點之間通過若干條邊(edge)連接起來,每條edge表示不同的操作(用\(o\)表示),比如卷積或者池化操作等。DARTS的想法是每條edge都有一個權重(用\(\alpha\)表示),而且權重是可以通過梯度更新的,最后會根據權重來選擇節點之間的操作,計算公式如下:
乍看起來好像挺好的,但是有一個問題。為方便討論,我們僅討論兩個節點的情況,我們假設一共有3個候選操作,且三個操作的權重隨機初始化為[0.2,0.3,0.5]。在經過一波訓練后,權重得到了更新變成了[0.1,0.2,0.7],這表示第三個操作的可能效果更好,所以應該以更大的概率選擇第三個操作。
二、DARTS缺點
可是DARTS算法在更新權重的過程中是並不是根據概率選擇操作的,而是向上面的公式一樣把所有操作乘上對應的權重得到mixed的結果,在權重更新結束后會簡單地只保留每組節點之間權重最大的那個操作。這樣一來有兩個問題:
1)每次更新都是對所有操作進行更新,這導致內存消耗更大;
2)最后只是簡單地選擇權重最大的操作,那么[0.2,0.3,0.5]和[0.1,0.2,0.7]並沒有本質的區別了,而且這樣一來可能第一個和第二個操作根本就沒有機會得到更新,但是從概率上來說這兩個權重分布差別是巨大的。
所以一個很自然的想法就是我們希望以0.1的概率選擇第一個操作,0.2的概率選擇第二個操作,0.7的概率選擇第三個操作。實現起來其實也挺簡單的,直接用np.random.choice就可以按照一定概率隨機選取操作。可是這樣一來又產生了一個新的問題,即這種隨機采樣的方式沒法計算梯度。
為什么沒法計算梯度呢?我們考慮如下簡單情況寫一下表達式:
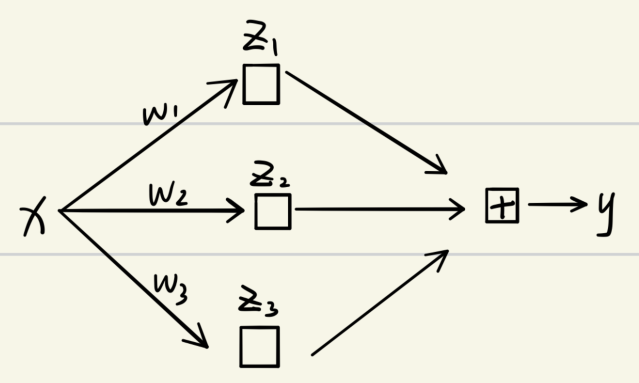
- DARTS的計算表達式,可以看到是可以順利求導的
- 以一定概率隨機采樣的表達式(右邊表示概率),可以看到這種隨機采樣無法求出概率。
三、Gumbel softmax登場
為了解決上面無法求導的問題,Gumbel softmax登場。它主要是使用了重參數技巧(Re-parameterization Trick)。
舉個簡單的栗子來幫助理解重參數技巧(gumbel softmax比這要稍微復雜一點,不過原理是一樣的):
假設現在求得的權重分布是\(W=[0.1,0.2,0.7]\)。
然后再假設我們可以根據某種分布對每個權重采樣一個隨機值,比如三個權重對應的采樣的隨機值分別是\(\epsilon=[0.5,0.6,0.05]\),我們把這些隨機值和權重相加之后得到\(\hat{W}=[0.1+0.5,0.2+0.6,0.7+0.05]=[0.6,0.8,0.75]\)。所以\(\hat{W}=W+\epsilon, \epsilon \thicksim P(某種分布)\),一般這個分布可以是0到1之間的均勻分布,即\(\epsilon \thicksim U(0,1)\)。
之后我們對采樣隨機值后的權重分布取\(argmax(\hat{W})\)的話應該是選擇第二個操作,當然這種概率是比較小的,這個也叫Gumbel-Max trick。可是argmax也有無法求導的問題,因此可以使用softmax來代替,也就是Gumbel-Softmax trick,那么有如下計算公式(\(\tau\)表示溫度系數,類似於知識蒸餾里的溫度系數,也是用來控制分布的平滑度)
我們現在再來看看使用gumbel softmax后的求導表達式:
所以gumbel softmax成功地引入了隨機性,使得每個操作都能以一定的概率被選中,不過貌似也並沒有減少內存的消耗,因為還是和DARTS一樣計算的mixed值。所以在GDAS這篇論文里作者在選擇操作的時候使用的是argmax,而在更新權重的時候采用的是softmax的梯度值,這個可以通過修改pytorch的backward部分代碼實現。
總結起來Gumbel-softmax在具體實踐上和上面的例子有一丟丟不一樣,總結起來步驟如下:
- 對於網絡輸出的一個n維向量\(v\),生成n個服從均勻分布\(U(0,1)\)的獨立樣本\(\epsilon_1,...,\epsilon_n\)
- 通過\(G_i=−log(−log(\epsilon_i))\)計算得到\(G_i\)
- 對應相加得到新的值向量\(v′=[v_1+G_1,v_2+G_2,...,v_n+G_n]\)
- 計算softmax函數
參考:
為什么gumbel-softmax技巧有效的證明可以參考如下文章
