概述
在學習法線貼圖的過程中,有幾個比較難以理解的概念,這里記錄一下。特別說一下,本文的法線貼圖是切線空間下的法線貼圖。
空間變換

如上圖所示,簡單表達了在使用法線貼圖的過程中,涉及到的幾個空間變換:
-
切線空間:從法線貼圖中采樣得到的法線,在切線空間中;
-
對象空間:物體的本地坐標空間,頂點的相關信息,在對象空間;
-
世界空間:光源位置、觀察者位置等,在世界空間中。
在空間變換的過程中,主要涉及到了兩個變換矩陣:
-
\(TBN\)矩陣:從切線空間變換到對象空間;
-
\(Model\)矩陣:從對象空間變換到世界空間。
對於上述概念,大部分都是比較熟悉的,只有法線貼圖、切線空間和\(TBN\)矩陣比較陌生。下面,將分別介紹一下。
法線貼圖
在3D計算機圖形學中,法線貼圖是一種用於偽造凹凸光照的技術,是凹凸貼圖的一種實現。它用於添加細節,而不使用更多的多邊形。這種技術的一個常見用途是,通過從高精度多邊形或高度圖生成法線貼圖,來極大地增強低精度多邊形的外觀和細節。下圖來自Paolo Cignoni,圖中對比了兩種方式:
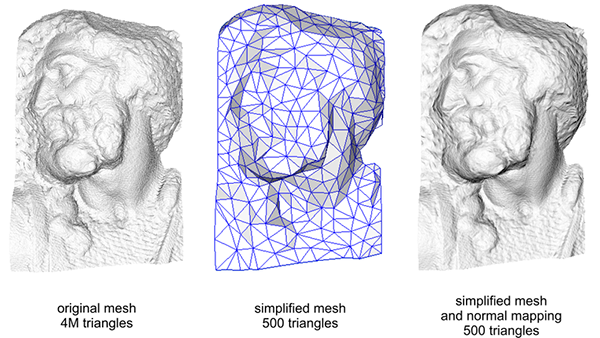
法線貼圖通常存儲為常規RGB圖像,其中RGB分量分別對應於表面法線的X,Y和Z坐標。
法線的每個分量的值的范圍是\([-1,1]\),而RGB分量的值的范圍是\([0,1]\)。所以,在將法線存儲為RGB圖像時,需要對每個分量做一個映射:
這里要注意,將法線存儲到法線貼圖的過程中,需要進行上述操作。當我們從法線貼圖中讀取到法線數據后,需要進行上述變換的逆變換,即從\([0,1]\)映射到\([-1,1]\)。
切線空間
那么,法線向量應該相對於哪個坐標系呢?我們可以選擇模型頂點的的坐標系,即對象空間;也可以選擇模型紋理所在的坐標系,即切線空間,也稱為紋理空間。
對象空間中,法線信息是相對於對象空間的朝向的,各個方向的法線向量都有,所有貼圖看起來色彩比較豐富;而在切線空間中,法線是相對於頂點的,大致指向頂點信息中的法線方向,即法線向量接近於\((0,0,1)\),映射到RGB是\((0.5,0.5,1)\),這是一種偏藍的顏色。下圖分別是對象空間和切線空間下的法線紋理。
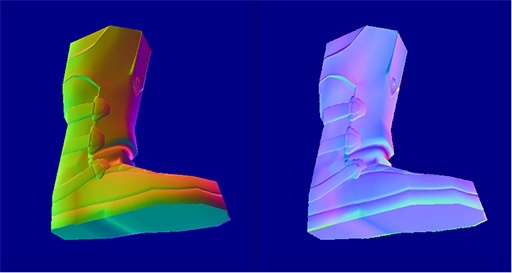
那么,怎么進行選擇呢?考慮一下二者的優缺點:
-
重用性:對於對象空間的法線貼圖,它是相對於特定對象的,假如應用到其他的對象上,可能效果就不正確了;而切線空間中的法線貼圖,記錄的是相對法線信息,所以可以把它應用到其他對象上,也能得到正確的結果。
-
可壓縮:考慮到法線向量是單位向量,而且Z分量總是正的,可以只存儲XY方向,而推導出Z方向。
綜上所述,我們一般選擇切線空間下的法線貼圖。
\(TBN\)矩陣
在光照的計算過程中,需要用到光線方向、視線方向和法線方向等,為了得到正確的結果,這些變量必須在同一坐標系下計算。參考一下本文開頭的“坐標變換示意圖”。
在紋理坐標系中,x和y分量與2D圖片的水平方向和垂直方向對齊,而z分量指向圖片外部的上方。如下圖所示:
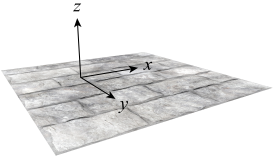
為了正確使用貼圖中的紋理信息,我們必須找到一種方法——從切線坐標空間變換到對象空間。這可以通過指定切線坐標系的坐標軸在對象空間中的方向來達到。
對一個單獨的三角形面片來說,我們可以認為紋理貼圖覆蓋在三角形的表面上,如下圖所示:

根據上圖,可以得出:三角面片和紋理貼圖是共面的。那么,根據平行四邊形法則,可以得出:
其中,\(E_{1}\)和\(E_{2}\)是兩個頂點之間的向量差,可以根據頂點的坐標計算出來;\(\Delta U_{1}\)、\(\Delta V_{1}\)、\(\Delta U_{2}\)和\(\Delta V_{2}\)分別是紋理坐標的水平和垂直方向的差,可以根據紋理坐標計算得到。\(U\)和\(V\)分別是紋理的水平和垂直坐標軸,是要計算的未知量。
寫成坐標表示:
上面的方程,也可以寫成矩陣乘法的形式:
兩邊同時乘以\(\Delta U \Delta V\)的逆矩陣,可得:
求逆矩陣不太方便,可以使用伴隨矩陣法:
至此,我們求出了\(U\)和\(V\)向量。但是我們需要的構成\(TBN\)空間的坐標軸是正交的,這里求出的\(U\)和\(V\)並不一定能滿足正交的條件。這里,頂點的法線\(N\)是已知的,我們可以根據\(U\)、\(V\)和\(N\),根據格拉姆-施密特正交化方法,求出與\(N\)正交的\(T\)和\(B\)(此處假設切線空間是右手坐標系):
這樣,我們獲得了坐標軸相互正交的\(TBN\)矩陣。
實際使用中的法線貼圖
看完上面計算切線空間的\(TBN\)矩陣的部分,估計也是頭大。不禁想到,每次使用法線貼圖的過程,真的如此麻煩嗎?
幸運的是,答案是否定的。
一般情況下,模型存儲的頂點信息中,都包含了頂點的法線和切線的數據,這樣,我們就不用進行上面的復雜計算了,直接使用法線和切線的叉乘,求出副切線,從而構成\(TBN\)矩陣。
