時間序列分析算法

簡介

在商業應用中，時間是最重要的因素，能夠提升成功率。然而絕大多數公司很難跟上時間的腳步。但是隨着技術的發展，出現了很多有效的方法，能夠讓我們預測未來。不要擔心，本文並不會討論時間機器，討論的都是很實用的東西。
本文將要討論關於預測的方法。有一種預測是跟時間相關的，而這種處理與時間相關數據的方法叫做時間序列模型。這個模型能夠在與時間相關的數據中，尋到一些隱藏的信息來輔助決策。
當我們處理時序序列數據的時候，時間序列模型是非常有用的模型。大多數公司都是基於時間序列數據來分析第二年的銷售量，網站流量，競爭地位和更多的東西。然而很多人並不了解的時間序列分析這個領域。
所以，如果你不了解時間序列模型。這篇文章將會想你介紹時間序列模型的處理步驟以及它的相關技術。
本文包含的內容如下所示：
目錄
* 1、時間序列模型介紹
* 2、使用R語言來探索時間序列數據
* 3、介紹ARMA時間序列模型
* 4、ARIMA時間序列模型的框架與應用

讓我們開始吧

1、時間序列模型介紹

Let’s begin。本節包括平穩序列，隨機游走,Rho系數,Dickey Fuller檢驗平穩性。如果這些知識你都不知道，不用擔心-接下來這些概念本節都會進行詳細的介紹，我敢打賭你很喜歡我的介紹的。

Return Top

平穩序列

判斷一個序列是不是平穩序列有三個評判標准：
1. 均值 ，是與時間t 無關的常數。下圖（左）滿足平穩序列的條件，下圖（右）很明顯具有時間依賴。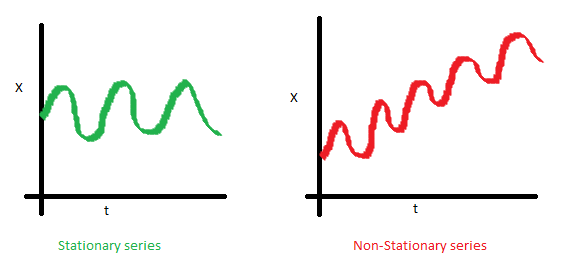

1. 方差 ，是與時間t 無關的常數。這個特性叫做方差齊性。下圖顯示了什么是方差對齊，什么不是方差對齊。（注意右手邊途中的不同分布。）
   

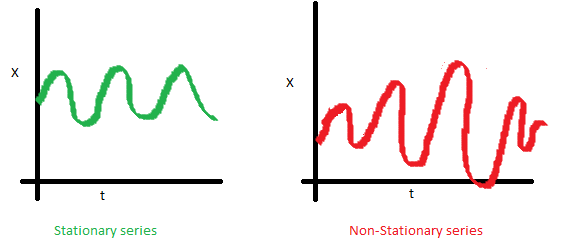
2. 協方差 ，只與時期間隔k有關，與時間t 無關的常數。如下圖（右），可以注意到隨着時間的增加，曲線變得越來越近。因此紅色序列的協方差並不是恆定的。
   

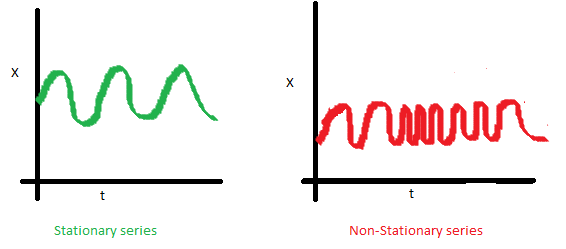
我們為什么要關心平穩時間序列呢？

除非你的時間序列是平穩的，否則不能建立一個時間序列模型。在很多案例中時間平穩條件常常是不滿足的，所以首先要做的就是讓時間序列變得平穩，然后嘗試使用隨機模型預測這個時間序列。有很多方法來平穩數據，比如消除長期趨勢，差分化。

Return Top

隨機游走

這是時間序列最基本的概念。你可能很了解這個概念。但是，很多工業界的人仍然將隨機游走看做一個平穩序列。在這一節中，我會使用一些數學工具，幫助理解這個概念。我們先看一個例子
例子：想想一個女孩隨機的在想象一個女孩在一個巨型棋盤上面隨意移動。這里，下一個位置只取決於上一個位置。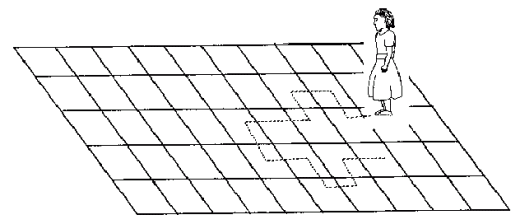

(來源:  http://scifun.chem.wisc.edu/WOP/RandomWalk.html )

現在想象一下，你在一個封閉的房間里，不能看見這個女孩。但是你想要預測不同時刻這個女孩的位置。怎么才能預測的准一點？當然隨着時間的推移你預測的越來越不准。在t=0時刻，你肯定知道這個女孩在哪里。下一個時刻女孩移動到附件8塊方格中的一塊，這個時候，你預測到的可能性已經降為1/8。繼續往下繼續預測，現在我們將這個序列公式化：

1 2	$X(t) = X(t-1) + Er(t)$ 這里的$Er_t$代表這這個時間點隨機干擾項。這個就是女孩在每一個時間點帶來的隨機性。

 

現在我們遞歸所有x時間點，最后我們將得到下面的等式：

1	$X(t) = X(0) + Sum(Er(1),Er(2),Er(3).....Er(t))$

 

現在，讓我們嘗試驗證一下隨機游走的平穩性假設：
1. 是否均值為常數？

1	E[X(t)] = E[X(0)] + Sum(E[Er(1)],E[Er(2)],E[Er(3)].....E[Er(t)])

 

我們知道由於隨機過程的隨機干擾項的期望值為0.到目前為止：E[X(t)] = E[X(0)] = 常數
2. 是否方差為常數？

1 2	Var[X(t)] = Var[X(0)] + Sum(Var[Er(1)],Var[Er(2)],Var[Er(3)].....Var[Er(t)]) Var[X(t)] = t * Var(Error) = 時間相關

 

因此，我們推斷，隨機游走不是一個平穩的過程，因為它有一個時變方差。此外，如果我們檢查的協方差，我們看到協方差依賴於時間。

我們看一個更有趣的東西

我們已經知道一個隨機游走是一個非平穩的過程。讓我們在方程中引入一個新的系數，看看我們是否能制定一個檢查平穩性的公式。
Rho系數

1	X(t) = Rho * X(t-1) + Er(t)

 

現在，我們將改變Rho看看我們可不可以讓這個序列變的平穩。這里我們只是看，並不進行平穩性檢驗。
讓我們從一個Rho=0的完全平穩序列開始。這里是時間序列的圖：

將Rho的值增加到0.5，我們將會得到如下圖：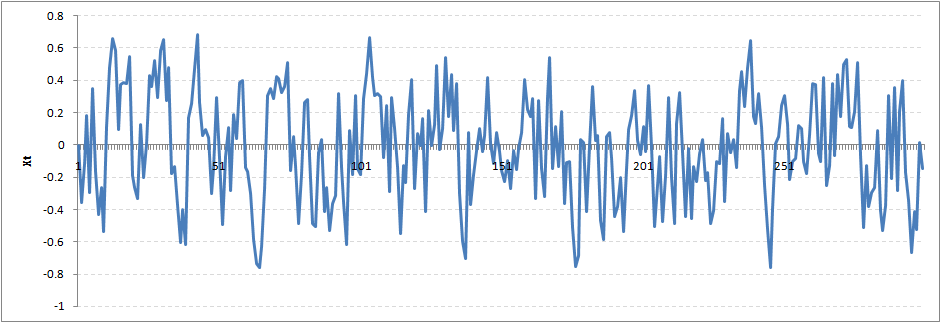

你可能會注意到，我們的周期變長了，但基本上似乎沒有一個嚴重的違反平穩性假設。現在讓我們采取更極端的情況下ρ= 0.9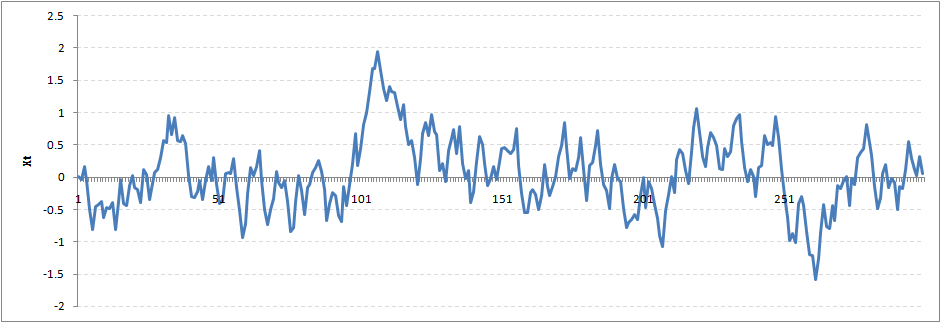

我們仍然看到，在一定的時間間隔后，從極端值返回到零。這一系列也不違反非平穩性明顯。現在，讓我們用ρ= 1隨機游走看看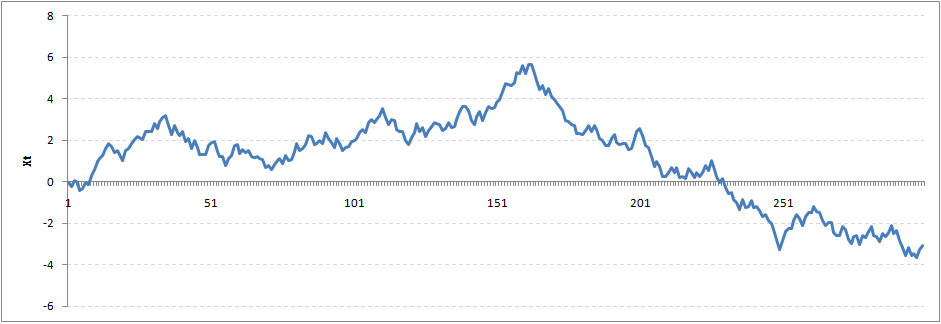

這顯然是違反固定條件。是什么使rho= 1變得這么特殊的呢？，這種情況並不滿足平穩性測試？我們來找找這個數學的原因
公式X(t) = Rho * X(t-1) + Er(t)的期望為：

1	E[X(t)] = Rho *E[ X(t-1)]

 

這個公式很有意義。下一個X(或者時間點t)被拉到Rho*上一個x的值。
例如，如果x（t–1）= 1，E[X（T）] = 0.5（Rho= 0.5）。現在，如果從零移動到任何方向下一步想要期望為0。唯一可以讓期望變得更大的就是錯誤率。當Rho變成1呢？下一步沒有任何可能下降。

Return Top

Dickey Fuller Test平穩性

這里學習的最后一個知識點是Dickey Fuller檢驗。。在統計學里，Dickey-Fuller檢驗是測試一個自回歸模型是否存在單位根。這里根據上面Rho系數有一個調整，將公式轉換為Dickey-Fuller檢驗

1 2	X(t) = Rho * X(t-1) + Er(t) =>  X(t) - X(t-1) = (Rho - 1) X(t - 1) + Er(t)

 

我們要測試如果Rho–1=0是否差異顯著。如果零假設不成立，我們將得到一個平穩時間序列。
平穩性測試和將一個序列轉換為平穩性序列是時間序列模型中最重要的部分。因此需要記住本節提到的所有概念方便進入下一節。
接下來就看看時間序列的例子。

2、使用R探索時間序列

本節我們將學習如何使用R處理時間序列。這里我們只是探索時間序列，並不會建立時間序列模型。
本節使用的數據是R中的內置數據：AirPassengers。這個數據集是1949-1960年每個月國際航空的乘客數量的數據。

Return Top

在入數據集

下面的代碼將幫助我們在入數據集並且能夠看到一些少量的數據集。

 1 > data(AirPassengers)#在入數據  2 > class(AirPassengers)  3 [1] "ts"  4 #查看AirPassengers數據類型，這里是時間序列數據  5 > start(AirPassengers)  6 [1] 1949 1  7 #這個是Airpassengers數據開始的時間  8 > end(AirPassengers)  9 [1] 1960 12 10 #這個是Airpassengers數據結束的時間 11 > frequency(AirPassengers) 12 [1] 12 13 #時間序列的頻率是一年12個月 14 > summary(AirPassengers) 15  Min. 1st Qu. Median Mean 3rd Qu. Max. 16 104.0 180.0 265.5 280.3 360.5 622.0

 

Return Top

矩陣中詳細數據

1 #The number of passengers are distributed across the spectrum 2 > plot(AirPassengers) 3 #繪制出時間序列 4 >abline(reg=lm(AirPassengers~time(AirPassengers))) 5 # 擬合一條直線

 

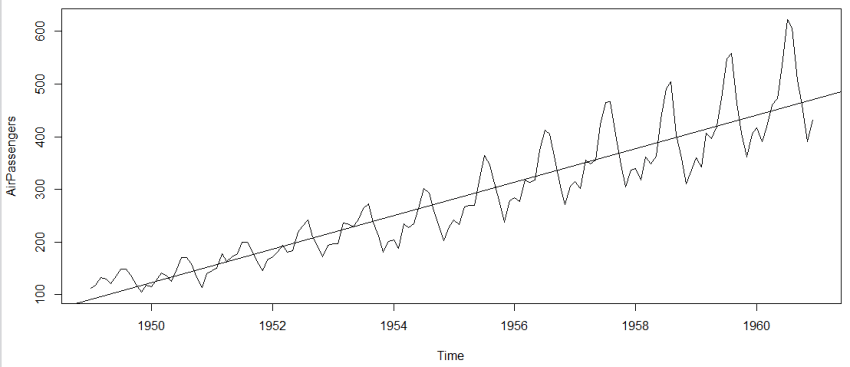
 1 > cycle(AirPassengers)  2  Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec  3 1949 1 2 3 4 5 6 7 8 9 10 11 12  4 1950 1 2 3 4 5 6 7 8 9 10 11 12  5 1951 1 2 3 4 5 6 7 8 9 10 11 12  6 1952 1 2 3 4 5 6 7 8 9 10 11 12  7 1953 1 2 3 4 5 6 7 8 9 10 11 12  8 1954 1 2 3 4 5 6 7 8 9 10 11 12  9 1955 1 2 3 4 5 6 7 8 9 10 11 12 10 1956 1 2 3 4 5 6 7 8 9 10 11 12 11 1957 1 2 3 4 5 6 7 8 9 10 11 12 12 1958 1 2 3 4 5 6 7 8 9 10 11 12 13 1959 1 2 3 4 5 6 7 8 9 10 11 12 14 1960 1 2 3 4 5 6 7 8 9 10 11 12 15 #打印每年的周期 16 > plot(aggregate(AirPassengers,FUN=mean)) 17 #繪制 18 > boxplot(AirPassengers~cycle(AirPassengers)) 19 #繪制盒圖

 

Return Top

重要推論

1. 每年的趨勢顯示旅客的數量每年都在增加
2. 七八月的均值和方差比其他月份要高很多
3. 每個月的平均值並不相同，但是方差差異很小。因此，可以看出具有很強的周期性。，一個周期為12個月或更少。

查看數據，試探數據是建立時間序列模型最重要的一部-如果沒有這一步，你將不知道這個序列是不是平穩序列。就像這個例子一樣，我們已經知道了很多關於這個模型的很多細節。
接下來我們會建立一些時間序列模型以及這些模型的特征，也會最一些預測。

3、ARMA時間序列模型

ARMA也叫自回歸移動平均混合模型。ARMA模型經常在時間序列中使用。在ARMA模型中，AR代表自回歸，MA代表移動平均。如果這些術語聽起來很復雜，不用擔心-下面將會用幾分鍾的時間簡單介紹這些概念。
我們現在就會領略這些模型的特點。在開始之前，你首先要記住，AR或者MA並不是應用在非平穩序列上的。
在實際應用中可能會得到一個非平穩序列，你首先要做的就是將這個序列變成平穩序列（通過差分化/轉換），然后選擇可以使用的時間序列模型。
首先，本文將介紹分開介紹兩個模型（AR&MA）。接下來我們看一看這些模型的特點。

Return Top

自回歸時間序列模型

讓我們從下面的例子理解AR模型：
現狀一個國家的GDP（x(t)）依賴與去年的GDP（x(t-1)).這個假設一個國家今年的GDP總值依賴與去年的GDP總值和今年的新開的工廠和服務。但是GDP的主要依賴與去年去年的GDP。
那么，GDP的公式為：

1	x(t) = alpha *  x(t – 1) + error (t)       （1）

 

這個等式就是AR公式。公式（1）表示下一個點完全依賴與前面一個點。alpha是一個系數，希望能夠找到alpha最小化錯誤率。x(t-1)同樣依賴x(t)。
例如，x(t)代表一個城市在某一天的果汁的銷售量。在冬天，極少的供應商進果汁。突然有一天，溫度上升了，果汁的需求猛增到1000.然而過了幾天，氣溫有下降了。但是眾所周知，人們在熱天會喝果汁，這些人會有50%在冷天仍然喝果汁。在接下來的幾天，這個比例降到了25%(50%的50%），然后幾天后逐漸降到一個很小的數。下圖解釋了AR序列的慣性：

Return Top

移動平均時間序列模型

接下來另一個關於移動平均的例子。
一個公司生成某種類型的包，這個很容易理解。作為一個競爭的市場，包的銷售量從零開始增加的。所以，有一天他做了一個實驗，設計並制作了不同的包，這種包並不會被隨時購買。因此，假設市場上總需求是1000個這種包。在某一天，這個包的需求特別高，很快庫存快要完了。這天結束了還有100個包沒賣掉。我們把這個誤差成為時間點誤差。接下來的幾天仍有幾個客戶購買這種包。下面通過一個簡單的公式來描述這個場景：

1	x(t) = beta *  error(t-1) + error (t)

 

嘗試把這個圖畫出來，就是這個樣子的：

注意到MA和AR模型的不同了沒？在MA模型中，噪聲/沖擊迅速小時。在AR模型中會受到長時間的影響。

Return Top

AR模型與MA模型的不同

AR與MA模型的主要不同在於時間序列對象在不同時間點的相關性。
MA模型用過去各個時期的隨機干擾或預測誤差的線性組合來表達當前預測值。當n>某一個值時，x(t)與x(t-n)的相關性總為0.AM模型僅通過時間序列變量的自身歷史觀測值來反映有關因素對預測目標的影響和作用，步驟模型變量相對獨立的假設條件約束，所構成的模型可以消除普通回退預測方法中由於自變量選擇、多重共線性等造成的困難。即AM模型中x(t)與x(t-1)的相關性隨着時間的推移變得越來越小。這個差別要好好利用起來。

Return Top

利用ACF和PACF繪圖

一旦我們得到一個平穩時間序列。我們必須要回答兩個最重要的問題；
Q1：這個是AR或者MA過程？
Q2：我們需要利用的AR或者MA過程的順序是什么？

解決這兩個問題我們要借助兩個系數：
時間序列x(t)滯后k階的樣本自相關系數（ACF）和滯后k期的情況下樣本偏自相關系數（PACF）。公式省略。
AR模型的ACF和PACF：
通過計算證明可知：
- AR的ACF為拖尾序列，即無論滯后期k取多大，ACF的計算值均與其1到p階滯后的自相關函數有關。
- AR的PACF為截尾序列，即當滯后期k>p時PACF=0的現象。

上圖藍線顯示值與0具有顯著的差異。很顯然上面PACF圖顯示截尾於第二個滯后，這意味這是一個AR（2）過程。
MA模型的ACF和PACF：
- MA的ACF為截尾序列，即當滯后期k>p時PACF=0的現象。
- AR的PACF為拖尾序列，即無論滯后期k取多大，ACF的計算值均與其1到p階滯后的自相關函數有關。

很顯然，上面ACF圖截尾於第二個滯后，這以為這是一個MA（2）過程。
目前，本文已經介紹了關於使用ACF&PACF圖識別平穩序列的類型。現在，我將介紹一個時間序列模型的整體框架。此外，還將討論時間序列模型的實際應用。

4、ARIMA時間序列模型的框架與應用

到此，本文快速介紹了時間序列模型的基礎概念、使用R探索時間序列和ARMA模型。現在我們將這些零散的東西組織起來，做一件很有趣的事情。

Return Top

框架

下圖的框架展示了如何一步一步的“做一個時間序列分析”

前三步我們在前文意見討論了。盡管如此，這里還是需要簡單說明一下：

第一步：時間序列可視化

在構建任何類型的時間序列模型之前，分析其趨勢是至關重要的。我們感興趣的細節包括序列中的各種趨勢、周期\季節性或者隨機行為。在本文的第二部分已經介紹了。

第二步：序列平穩

一旦我們知道了模式、趨勢、周期。我們就可以檢查序列是否平穩。Dicky-Fuller是一種很流行的檢驗方式。在第一部分意見介紹了這種檢驗方式。在這里還沒有結束！如果發現序列是非平穩序列怎么辦？
這里有三種比較常用的技術來讓一個時間序列平穩。
1 消除趨勢：這里我們簡單的刪除時間序列中的趨勢成分。例如，我的時間序列的方程是：

1	x(t) = (mean + trend * t) + error

 

這里我簡單的刪除上述公式中的trend*t部分，建立x(t)=mean+error模型
2 差分：這個技術常常用來消除非平穩性。這里我們是對序列的差分的結果建立模型而不是真正的序列。例如：

1	x(t) – x(t-1) = ARMA (p ,  q)

 

這個差分也是ARIMA的部分。現在我們有3個參數了：

1 2 3

p:AR d:I q:MA

 

3 季節性：季節性直接被納入ARIMA模型中。下面的應用部分我們再討論這個。

第三步：找到最優參數

參數p,q可以使用ACF和PACF圖發現。除了這種方法，如果相關系數ACF和偏相關系數PACF逐漸減小，這表明我們需要進行時間序列平穩並引入d參數。

第四步：簡歷ARIMA模型

找到了這些參數，我們現在就可以嘗試簡歷ARIMA模型了。從上一步找到的值可能只是一個近似估計的值，我們需要探索更多(p,d,q）的組合。最小的BIC和AIC的模型參數才是我們要的。我們也可以嘗試一些季節性成分。在這里，在ACF/PACF圖中我們會注意到一些季節性的東西。

第五步：預測

到這步，我們就有了ARIMA模型，我們現在就可以做預測了。我們也可以將這種趨勢可視化，進行交叉驗證。

Return Top

時間序列模型的應用。

這里我們用前面的例子。使用這個時間序列做預測。我們建議你在進行下一步之前，先觀察這個數據。

我們從哪里開始呢？

下圖是這些年的乘客數的圖。在往下看之前，觀察這個圖。

這里是我的觀察：
1. 乘客有着逐年增加的趨勢。
2. 這看起來有季節性，每一個周期不超過12個月。
3. 數據的方差逐年增加。
在我們進行平穩性測試之前我們需要解決兩個問題。第一，我們需要消除方差不齊。這里我們對這個序列做求對數。第二我們需要解決序列的趨勢性。我們通過對時序序列做差分。現在，我們來檢驗最終序列的平穩性。

1 adf.test(diff(log(AirPassengers)), alternative="stationary", k=0) 2 #這里可能會顯示沒有這個函數，需要安裝一下.install.packages("tseries") 3 #加在這個包,library(tseries 4  data: diff(log(AirPassengers)) 5 Dickey-Fuller = -9.6003, Lag order = 0, 6 p-value = 0.01 7 alternative hypothesis: stationary

 

我們可以看出這個序列是足夠平穩做任何時間序列模型。
下一步就是找到ARIMA模型的正確的參數。我們意見知道’d‘是1，因此我們需要做1差分讓序列平穩。這里我們繪制出相關圖。下面就是這個序列的ACF圖。

1 2	#ACF圖 acf(log(AirPassengers))

 

從上述表格可以看出什么？

很顯然ACF下降的十分的慢，這就意味着乘客的數量並不是平穩的。我們在前面已經討論了，我們現狀准備在序列去對數后的差分上做回歸，而不是直接在序列去對數后的數據熵差分。讓我們看一下差分后的ACF和PACF曲線吧。

1 2	> acf(diff(log(AirPassengers))) > pacf(diff(log(AirPassengers)))

 

顯然ACF截止與第一個滯后，因此我們知道p的值應該是0.而q的值應該是1或者2.幾次迭代以后，我們發現(p,d,q)取(0,1,1)時，AIC和BIC最小。

1 > fit <- arima(log(AirPassengers), c(0, 1, 1),seasonal = list(order = c(0, 1, 1), period = 12)) 2 > pred <- predict(fit, n.ahead = 10*12) 3 ts.plot(AirPassengers,2.718^pred$pred, log = "y", lty = c(1,3))