過擬合、欠擬合及其解決方案

1. 過擬合、欠擬合的概念
2. 權重衰減
3. 丟棄法

模型選擇、過擬合和欠擬合

訓練誤差和泛化誤差

在解釋上述現象之前，我們需要區分訓練誤差（training error）和泛化誤差（generalization error）。通俗來講，前者指模型在訓練數據集上表現出的誤差，后者指模型在任意一個測試數據樣本上表現出的誤差的期望，並常常通過測試數據集上的誤差來近似。計算訓練誤差和泛化誤差可以使用之前介紹過的損失函數，例如線性回歸用到的平方損失函數和softmax回歸用到的交叉熵損失函數。

機器學習模型應關注降低泛化誤差。

模型選擇

驗證數據集

從嚴格意義上講，測試集只能在所有超參數和模型參數選定后使用一次。不可以使用測試數據選擇模型，如調參。由於無法從訓練誤差估計泛化誤差，因此也不應只依賴訓練數據選擇模型。鑒於此，我們可以預留一部分在訓練數據集和測試數據集以外的數據來進行模型選擇。這部分數據被稱為驗證數據集，簡稱驗證集（validation set）。例如，我們可以從給定的訓練集中隨機選取一小部分作為驗證集，而將剩余部分作為真正的訓練集。

K折交叉驗證

由於驗證數據集不參與模型訓練，當訓練數據不夠用時，預留大量的驗證數據顯得太奢侈。一種改善的方法是K折交叉驗證（K-fold cross-validation）。在K折交叉驗證中，我們把原始訓練數據集分割成K個不重合的子數據集，然后我們做K次模型訓練和驗證。每一次，我們使用一個子數據集驗證模型，並使用其他K-1個子數據集來訓練模型。在這K次訓練和驗證中，每次用來驗證模型的子數據集都不同。最后，我們對這K次訓練誤差和驗證誤差分別求平均。

過擬合和欠擬合

接下來，我們將探究模型訓練中經常出現的兩類典型問題：

• 一類是模型無法得到較低的訓練誤差，我們將這一現象稱作欠擬合（underfitting）；
• 另一類是模型的訓練誤差遠小於它在測試數據集上的誤差，我們稱該現象為過擬合（overfitting）。
  在實踐中，我們要盡可能同時應對欠擬合和過擬合。雖然有很多因素可能導致這兩種擬合問題，在這里我們重點討論兩個因素：模型復雜度和訓練數據集大小。

模型復雜度

為了解釋模型復雜度，我們以多項式函數擬合為例。給定一個由標量數據特征\(x\)和對應的標量標簽\(y\)組成的訓練數據集，多項式函數擬合的目標是找一個\(K\)階多項式函數

\[ \hat{y} = b + \sum_{k=1}^K x^k w_k \]

來近似 \(y\)。在上式中，\(w_k\)是模型的權重參數，\(b\)是偏差參數。與線性回歸相同，多項式函數擬合也使用平方損失函數。特別地，一階多項式函數擬合又叫線性函數擬合。

給定訓練數據集，模型復雜度和誤差之間的關系：

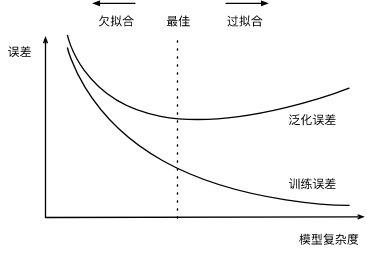
訓練數據集大小

影響欠擬合和過擬合的另一個重要因素是訓練數據集的大小。一般來說，如果訓練數據集中樣本數過少，特別是比模型參數數量（按元素計）更少時，過擬合更容易發生。此外，泛化誤差不會隨訓練數據集里樣本數量增加而增大。因此，在計算資源允許的范圍之內，我們通常希望訓練數據集大一些，特別是在模型復雜度較高時，例如層數較多的深度學習模型。

多項式函數擬合實驗

%matplotlib inline
import torch
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)

1.3.0

初始化模型參數

n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = torch.randn((n_train + n_test, 1))
poly_features = torch.cat((features, torch.pow(features, 2), torch.pow(features, 3)), 1) 
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
          + true_w[2] * poly_features[:, 2] + true_b)
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)

features[:2], poly_features[:2], labels[:2]

(tensor([[1.4491],
         [0.4249]]), tensor([[1.4491, 2.0999, 3.0430],
         [0.4249, 0.1805, 0.0767]]), tensor([16.6427,  5.3372]))

定義、訓練和測試模型

def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
             legend=None, figsize=(3.5, 2.5)):
    # d2l.set_figsize(figsize)
    d2l.plt.xlabel(x_label)
    d2l.plt.ylabel(y_label)
    d2l.plt.semilogy(x_vals, y_vals)
    if x2_vals and y2_vals:
        d2l.plt.semilogy(x2_vals, y2_vals, linestyle=':')
        d2l.plt.legend(legend)

num_epochs, loss = 100, torch.nn.MSELoss()

def fit_and_plot(train_features, test_features, train_labels, test_labels):
    # 初始化網絡模型
    net = torch.nn.Linear(train_features.shape[-1], 1)
    # 通過Linear文檔可知，pytorch已經將參數初始化了，所以我們這里就不手動初始化了
    
    # 設置批量大小
    batch_size = min(10, train_labels.shape[0])    
    dataset = torch.utils.data.TensorDataset(train_features, train_labels)      # 設置數據集
    train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True) # 設置獲取數據方式
    
    optimizer = torch.optim.SGD(net.parameters(), lr=0.01)                      # 設置優化函數，使用的是隨機梯度下降優化
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:                                                 # 取一個批量的數據
            l = loss(net(X), y.view(-1, 1))                                     # 輸入到網絡中計算輸出，並和標簽比較求得損失函數
            optimizer.zero_grad()                                               # 梯度清零，防止梯度累加干擾優化
            l.backward()                                                        # 求梯度
            optimizer.step()                                                    # 迭代優化函數，進行參數優化
        train_labels = train_labels.view(-1, 1)
        test_labels = test_labels.view(-1, 1)
        train_ls.append(loss(net(train_features), train_labels).item())         # 將訓練損失保存到train_ls中
        test_ls.append(loss(net(test_features), test_labels).item())            # 將測試損失保存到test_ls中
    print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])    
    semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
             range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('weight:', net.weight.data,
          '\nbias:', net.bias.data)

三階多項式函數擬合（正常）

fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :], labels[:n_train], labels[n_train:])

final epoch: train loss 9.372069325763732e-05 test loss 0.00013170466991141438
weight: tensor([[ 1.1970, -3.3981,  5.6008]]) 
bias: tensor([4.9985])

線性函數擬合（欠擬合）

fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train], labels[n_train:])

final epoch: train loss 217.625 test loss 1188.63232421875
weight: tensor([[16.4630]]) 
bias: tensor([1.7159])

訓練樣本不足（過擬合）

fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2], labels[n_train:])

final epoch: train loss 0.5842587351799011 test loss 873.285888671875
weight: tensor([[2.3961, 1.8384, 2.2060]]) 
bias: tensor([2.7476])

權重衰減

方法

權重衰減等價於 \(L_2\) 范數正則化（regularization）。正則化通過為模型損失函數添加懲罰項使學出的模型參數值較小，是應對過擬合的常用手段。

L2 范數正則化（regularization）

\(L_2\)范數正則化在模型原損失函數基礎上添加\(L_2\)范數懲罰項，從而得到訓練所需要最小化的函數。\(L_2\)范數懲罰項指的是模型權重參數每個元素的平方和與一個正的常數的乘積。以線性回歸中的線性回歸損失函數為例

\[ \ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2 \]

其中\(w_1, w_2\)是權重參數，\(b\)是偏差參數，樣本\(i\)的輸入為\(x_1^{(i)}, x_2^{(i)}\)，標簽為\(y^{(i)}\)，樣本數為\(n\)。將權重參數用向量\(\boldsymbol{w} = [w_1, w_2]\)表示，帶有\(L_2\)范數懲罰項的新損失函數為

\[\ell(w_1, w_2, b) + \frac{\lambda}{2n} |\boldsymbol{w}|^2, \]

其中超參數\(\lambda > 0\)。當權重參數均為0時，懲罰項最小。當\(\lambda\)較大時，懲罰項在損失函數中的比重較大，這通常會使學到的權重參數的元素較接近0。當\(\lambda\)設為0時，懲罰項完全不起作用。上式中\(L_2\)范數平方\(|\boldsymbol{w}|^2\)展開后得到\(w_1^2 + w_2^2\)。
有了\(L_2\)范數懲罰項后，在小批量隨機梯度下降中，我們將線性回歸一節中權重\(w_1\)和\(w_2\)的迭代方式更改為

\[ \begin{aligned} w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned} \]

可見，\(L_2\)范數正則化令權重\(w_1\)和\(w_2\)先自乘小於1的數，再減去不含懲罰項的梯度。因此，\(L_2\)范數正則化又叫權重衰減。權重衰減通過懲罰絕對值較大的模型參數為需要學習的模型增加了限制，這可能對過擬合有效。

高維線性回歸實驗從零開始的實現

下面，我們以高維線性回歸為例來引入一個過擬合問題，並使用權重衰減來應對過擬合。設數據樣本特征的維度為\(p\)。對於訓練數據集和測試數據集中特征為\(x_1, x_2, \ldots, x_p\)的任一樣本，我們使用如下的線性函數來生成該樣本的標簽：

\[ y = 0.05 + \sum_{i = 1}^p 0.01x_i + \epsilon \]

其中噪聲項\(\epsilon\)服從均值為0、標准差為0.01的正態分布。為了較容易地觀察過擬合，我們考慮高維線性回歸問題，如設維度\(p=200\)；同時，我們特意把訓練數據集的樣本數設低，如20。

%matplotlib inline
import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l

print(torch.__version__)

1.3.0

初始化模型參數

與前面觀察過擬合和欠擬合現象的時候相似，在這里不再解釋。

n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05

features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]

# 定義參數初始化函數，初始化模型參數並且附上梯度
def init_params():
    w = torch.randn((num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

定義L2范數懲罰項

def l2_penalty(w):
    return (w**2).sum() / 2

定義訓練和測試

batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss

dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)

def fit_and_plot(lambd):
    w, b = init_params()
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            # 添加了L2范數懲罰項
            l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
            l = l.sum()
            
            if w.grad is not None:
                w.grad.data.zero_()
                b.grad.data.zero_()
            l.backward()
            d2l.sgd([w, b], lr, batch_size)
        train_ls.append(loss(net(train_features, w, b), train_labels).mean().item())
        test_ls.append(loss(net(test_features, w, b), test_labels).mean().item())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', w.norm().item())

觀察過擬合

fit_and_plot(lambd=0)

L2 norm of w: 13.834592819213867

使用權重衰減

fit_and_plot(lambd=3)

L2 norm of w: 0.04155886918306351

簡潔實現

def fit_and_plot_pytorch(wd):
    # 對權重參數衰減。權重名稱一般是以weight結尾
    net = nn.Linear(num_inputs, 1)
    nn.init.normal_(net.weight, mean=0, std=1)
    nn.init.normal_(net.bias, mean=0, std=1)
    optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # 對權重參數衰減
    optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr)  # 不對偏差參數衰減
    
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            l = loss(net(X), y).mean()
            optimizer_w.zero_grad()
            optimizer_b.zero_grad()
            
            l.backward()
            
            # 對兩個optimizer實例分別調用step函數，從而分別更新權重和偏差
            optimizer_w.step()
            optimizer_b.step()
        train_ls.append(loss(net(train_features), train_labels).mean().item())
        test_ls.append(loss(net(test_features), test_labels).mean().item())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net.weight.data.norm().item())

fit_and_plot_pytorch(0)

L2 norm of w: 14.511220932006836

fit_and_plot_pytorch(3)

L2 norm of w: 0.06331753730773926

丟棄法

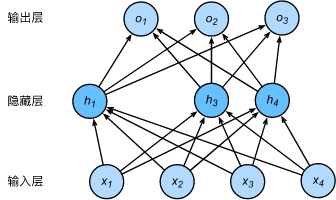
多層感知機中神經網絡圖描述了一個單隱藏層的多層感知機。其中輸入個數為4，隱藏單元個數為5，且隱藏單元\(h_i\)（\(i=1, \ldots, 5\)）的計算表達式為

\[ h_i = \phi\left(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_i\right) \]

這里\(\phi\)是激活函數，\(x_1, \ldots, x_4\)是輸入，隱藏單元\(i\)的權重參數為\(w_{1i}, \ldots, w_{4i}\)，偏差參數為\(b_i\)。當對該隱藏層使用丟棄法時，該層的隱藏單元將有一定概率被丟棄掉。設丟棄概率為\(p\)，那么有\(p\)的概率\(h_i\)會被清零，有\(1-p\)的概率\(h_i\)會除以\(1-p\)做拉伸。丟棄概率是丟棄法的超參數。具體來說，設隨機變量\(\xi_i\)為0和1的概率分別為\(p\)和\(1-p\)。使用丟棄法時我們計算新的隱藏單元\(h_i'\)

\[ h_i' = \frac{\xi_i}{1-p} h_i \]

由於\(E(\xi_i) = 1-p\)，因此

\[ E(h_i') = \frac{E(\xi_i)}{1-p}h_i = h_i \]

即丟棄法不改變其輸入的期望值。讓我們對之前多層感知機的神經網絡中的隱藏層使用丟棄法，一種可能的結果如圖所示，其中\(h_2\)和\(h_5\)被清零。這時輸出值的計算不再依賴\(h_2\)和\(h_5\)，在反向傳播時，與這兩個隱藏單元相關的權重的梯度均為0。由於在訓練中隱藏層神經元的丟棄是隨機的，即\(h_1, \ldots, h_5\)都有可能被清零，輸出層的計算無法過度依賴\(h_1, \ldots, h_5\)中的任一個，從而在訓練模型時起到正則化的作用，並可以用來應對過擬合。在測試模型時，我們為了拿到更加確定性的結果，一般不使用丟棄法

丟棄法從零開始的實現

%matplotlib inline
import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l

print(torch.__version__)

1.3.0

def dropout(X, drop_prob):
    X = X.float()
    assert 0 <= drop_prob <= 1
    keep_prob = 1 - drop_prob
    # 這種情況下把全部元素都丟棄
    if keep_prob == 0:
        return torch.zeros_like(X)
    mask = (torch.rand(X.shape) < keep_prob).float()
    
    return mask * X / keep_prob

X = torch.arange(16).view(2, 8)
dropout(X, 0)

tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])

dropout(X, 0.5)

tensor([[ 0.,  0.,  0.,  6.,  0., 10., 12.,  0.],
        [ 0.,  0., 20., 22.,  0.,  0.,  0.,  0.]])

dropout(X, 1.0)

tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

# 參數的初始化
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

W1 = torch.tensor(np.random.normal(0, 0.01, size=(num_inputs, num_hiddens1)), dtype=torch.float, requires_grad=True)
b1 = torch.zeros(num_hiddens1, requires_grad=True)
W2 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens1, num_hiddens2)), dtype=torch.float, requires_grad=True)
b2 = torch.zeros(num_hiddens2, requires_grad=True)
W3 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens2, num_outputs)), dtype=torch.float, requires_grad=True)
b3 = torch.zeros(num_outputs, requires_grad=True)

params = [W1, b1, W2, b2, W3, b3]

drop_prob1, drop_prob2 = 0.2, 0.5

def net(X, is_training=True):
    X = X.view(-1, num_inputs)
    H1 = (torch.matmul(X, W1) + b1).relu()
    if is_training:  # 只在訓練模型時使用丟棄法
        H1 = dropout(H1, drop_prob1)  # 在第一層全連接后添加丟棄層
    H2 = (torch.matmul(H1, W2) + b2).relu()
    if is_training:
        H2 = dropout(H2, drop_prob2)  # 在第二層全連接后添加丟棄層
    return torch.matmul(H2, W3) + b3

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        if isinstance(net, torch.nn.Module):
            net.eval() # 評估模式, 這會關閉dropout
            acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
            net.train() # 改回訓練模式
        else: # 自定義的模型
            if('is_training' in net.__code__.co_varnames): # 如果有is_training這個參數
                # 將is_training設置成False
                acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item() 
            else:
                acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() 
        n += y.shape[0]
    return acc_sum / n

num_epochs, lr, batch_size = 5, 100.0, 256  # 這里的學習率設置的很大，原因與之前相同。
loss = torch.nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root='/home/kesci/input/FashionMNIST2065')
d2l.train_ch3(
    net,
    train_iter,
    test_iter,
    loss,
    num_epochs,
    batch_size,
    params,
    lr)

epoch 1, loss 0.0044, train acc 0.564, test acc 0.738
epoch 2, loss 0.0023, train acc 0.790, test acc 0.763
epoch 3, loss 0.0019, train acc 0.821, test acc 0.825
epoch 4, loss 0.0017, train acc 0.841, test acc 0.787
epoch 5, loss 0.0016, train acc 0.850, test acc 0.836

簡潔實現

net = nn.Sequential(
        d2l.FlattenLayer(),
        nn.Linear(num_inputs, num_hiddens1),
        nn.ReLU(),
        nn.Dropout(drop_prob1),
        nn.Linear(num_hiddens1, num_hiddens2), 
        nn.ReLU(),
        nn.Dropout(drop_prob2),
        nn.Linear(num_hiddens2, 10)
        )

for param in net.parameters():
    nn.init.normal_(param, mean=0, std=0.01)

optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)

epoch 1, loss 0.0049, train acc 0.519, test acc 0.684
epoch 2, loss 0.0024, train acc 0.773, test acc 0.744
epoch 3, loss 0.0020, train acc 0.814, test acc 0.780
epoch 4, loss 0.0018, train acc 0.832, test acc 0.841
epoch 5, loss 0.0017, train acc 0.846, test acc 0.800

總結

• 欠擬合現象：模型無法達到一個較低的誤差

• 過擬合現象：訓練誤差較低但是泛化誤差依然較高，二者相差較大