Constraint Satisfaction Problem
在搜索算法中,我們關心的是從初始節點到目標節點的一條路徑;而在約束滿足問題中,我們沒有初始狀態,只關心 goal 而不在乎 path。
- Planning: sequences of actions
- Identification: assignments to variables
Constraint Satisfaction Problems (CSPs) are specialized for identification problems
我們可以把 CSP 看成是特殊的搜索問題。對於一般的搜索問題來說,State is atomic or indivisible, known as a “black box” without internal structure,而在 CSP 中 State is represented as a feature vector;在搜索問題中 Goal test can be any function over states,而CSP 中 Goal test is a set of constraints to identify the allowable feature vector。
我們來仔細看看 Feature Vector,它是由 A set of k variables (or features) 組成的,對於每個 feature 有值域 domain;而我們的目標就是找到滿足約束的一組賦值。方便起見我們定義 complete state 和 partial state,后者即對部分變量賦值滿足約束,其余部分待賦值。典型的問題有 Map Coloring 和 N-Queens 等。
Constraint Graphs
對於一個 CSP 問題,我們可以采用約束圖的方式進行表示:對於一個二元約束來說可將兩個 feature 連起來;所以,問題在於將 N-nary 轉化為 Binary constraints。我們假定 domain 都是有限的。
第一步,引入新的變量(約束)Z,例如對於加法的三元約束來說,我們引入變量,滿足
Domain is the set of all possible 3-tuples satisfying \(A+B=C\). \(\{(a_1 , b_1 , c _1 ), (a_ 2 , b _2 , c_ 2 ), …\}, s.t. a_ 1 + b_ 1 = c_ 1 …\)
第二步,建立新變量 Z 與 A、B、C 之間的約束,顯然可以是 A 與 Z 的 domain 中三元組的第一個元素相同。
Create new constraints between Z and three original variables respectively (the position in the tuple is linked to an original variable).
\[(Z,A)\in \{((a_1,b_1,c_1)a_1),...\}\tag{1}\\ (Z,B)\in \{((a_1,b_1,c_1)b_1),...\} \]
這樣,我們通過引入一個新的變量,和三個二元約束,就把該三元約束轉換好了;對於更多的約束,可以用相似的方法進行。
Note:這里可能一時沒法理解,我們要理解究竟什么是約束。先來看普通的二元約束,以地圖問題為例,假設每個國家的顏色均可為紅黃藍,約束的意義在於,若 A 填了紅色,那么相鄰的 B 就只能塗黃或藍——也就是說,一個變量的值確定后,另一個變量的值域也變化了——反過來想我們如何表示約束?可以采用集合的形式 \(\{(R,Y),(R,B)...\}\) 。我們重新來理解約束,就是 A 和 B 分別取值,構成一個二元組,要求這個二元組在約束集合中。(我在理解上的困惑實際上在於,沒有搞清楚約束的形式化表達。)這樣的話,我們來看加法約束,假設 A 已定,對於 A 和 Z 的約束來說,式(1)要求兩者構成的二元組要在約束集合中,這樣就縮減了 Z 的值域;若進一步定下了 B 的值,Z 的值域將進一步縮小,事實上這時僅可能剩下一個三元組 \((a,b,c=a+b)\) ,接下來可對 C 進行賦值或者檢測約束是否滿足。
Solving CSPs
我們可采用 Standard search formulation of CSPs,我們的初始狀態為一個 empty assignment,后繼函數為對任一未賦值變量進行賦值,而目標檢測則要求賦值為 complete state 且符合約束。顯然,1. 我們只檢查了葉節點而事實上在過程中就可以進行約束檢查;2. 如前所述,我們並不關心賦值的順序,只關心 goal。注意到無論是 BFS 還是 DFS 都是低效的,但是我們沒必要存儲中間節點,因此,要在 DFS 框架下進行改進。
Backtracking Search 算法針對了這兩個問題進行了改進
- Idea 1: One variable at a time in fixed ordering
- Idea 2: Check constraints as you go
簡言之:Backtracking = DFS + variable-ordering + fail-on-violation
兩個思路都是比較直觀的不多介紹。

現在的問題在於,如何 Improving Backtracking。
Ordering
顯見,不同的賦值順序會對效率產生影響,又可分為兩類:Which variable should be assigned next? In what order should its values be tried?
對於變量的順序來說,直觀來講,為了盡早避免可能的沖突,我們會選取那些約束比較多的變量(或者說,是 domain 比較小的,回憶一下約束的意義即在於,某一變量定值之后會縮減另外的變量的 domain)。例如,在地圖着色問題中,我們一般會從已着色的國家的相鄰國開始進行着色。定義:
Variable Ordering: Minimum remaining values (MRV)
Choose the variable with the fewest legal left values in its domain. Also called “most constrained variable”
“Fail-fast” ordering
對於賦值的順序來說,我們要盡早找到一組解(而不是回溯),那么我們肯定希望給剩余的變量更多的「可能性」,也就是說要避免其他變量的取值發生縮減;我們定義
Value Ordering: Least Constraining Value (LSV)
Given a choice of variable, choose the least constraining value. I.e., the one that rules out the fewest values in the remaining variables
Note that it may take some computation to determine this! (E.g., rerunning filtering)
注意,前者可以讓我們避免一些可能的錯誤(可以「剪枝」);而或者只是提高了找到解的可能性(但並非保障,只能說「更快找到」)。若我們想找到全部的解,那么前者可以幫助減少計算,但后者則並不會有什么助益。
Filtering: Can we detect inevitable failure early?
MRV 可以讓我們避免一些簡單的錯誤(如相鄰兩國填同樣的顏色),然而這里我們僅僅檢測了這樣一個簡單的約束;那么我們能否采取更多的計算來提前發現錯誤呢?這就是 Filtering 的思路。
我們先來看Forward Checking:Cross off values that violate a constraint when added to the existing assignment。我們在取定一個值(搜索)之后,對於相鄰邊的 domain 進行縮減(推理)。當然,這里我們只「向前看」了一步,事實上對於縮減了 domain 的變量我們可以繼續進行推理,也就是約束傳播 Constraint Propagation 。我們來給出定義:
Consistency of A Single Arc
An arc \(X \rightarrow Y\) is consistent iff for every \(x\) in the tail there is some \(y\) in the head which could be assigned without violating a constraint
Forward checking: Enforcing consistency of arcs pointing to each new assignment
注意定義,對於一條弧 \(X \rightarrow Y\) 來說,我們給定Y/減小了其值域之后,要進行縮減的是 X 的值域;如何縮減,就是要使得 X 的任一個取值,Y 中都至少有一個能滿足約束——對於那么不滿足的 X 的取值,我們進行縮減。注意其方向,按照這個定義,我們在做 Forward checking 的時候,給定了 A,那么就要對於所以包含指向 A 的弧(事實上都是無向邊)的變量進行值域縮減。下面給出具體的算法:
更宏觀的解釋:在 Filtering 中,我們交替進行搜索和推理,在為某一變量賦值之后做弧相容檢查。具體來說,當\(X_i\)賦值后,我們調用\(AC-3\),從\((X_j,X_i)\)中未賦值變量\(X_j\)開始,進行約束傳播;事實上我們維護了一個隊列,一旦某一個變量的值域發生了變化,就將其 neighbors 加入其中。
然而,弧相容仍不能保證不進行回溯。例如,對於一個三角形來說,若每個節點只能賦值為紅藍兩色那么顯然是無解的,但用弧相容找不錯錯誤來。若想直接得到解,我么引入k-相容 K-Consistency 的概念:
- 1-Consistency (Node Consistency): Each single node’s domain has a value which meets that node’s unary constraints
- 2-Consistency (Arc Consistency): For each pair of nodes, any consistent assignment to one can be extended to the other
- K-Consistency: For each k nodes, any consistent assignment to k-1 can be extended to the k th node.
並給出強 k-相容 Strong k-consistency: also k-1, k-2, … 1 consistent,以及結論,對於一個 n 變量的 CSP 來說,strong n-consistency means we can solve without backtracking。這是顯然的。
Structure: Can we exploit the problem structure?
這里問題的結果指的是約束圖的結構。考慮極端情況:所有節點結構獨立的,那么我們可以任意賦值;更為一般的,Independent sub-problems are identifiable as connected components of constraint graph。事實上,這樣可分割的情況是很少見的(如澳大利亞地圖着色),一個理想的可分問題能大大降低復雜度。注意到,我們可以用 Search 問題的通用復雜度來衡量 CSP,搜索樹的深度顯然是節點數,寬度為 domain 的大小;若一個 n 個節點的問題可分割成大小為 c 的若干子問題,則時間復雜度從 \(O(d^n)\) 降為 \(O({n \over c} d^c)\) ,變成了 n 的線性函數。
可分割為 sub-problems 的問題也是很少見的,一個更一般的情況是 Tree-Structured CSPs,對此我們有定理:
Theorem: if the constraint graph has no loops, the CSP can be solved in \(O(n d^2 )\) time
同樣變為了 n 的線性函數。如何做到呢?1. 對約束樹進行拓撲排序;2. 逆着拓撲排序,從孩子到父節點做弧相容檢查(即對於\((Parent(X_j),X_j)\)進行檢查);3. 然后順着拓撲排序,從根節點到到葉節點進行賦值。注意到,進行這樣一次弧相容檢查之后,我們保障了對於父節點的任意取值,子節點都至少有一個值滿足約束,也就保障了算法的正確性(解的存在性)。
樹結構也太少見了,一個拓展是 Nearly Tree-Structured CSPs 。對其的思路是,選定一組變量,使得刪去這些之后的節點構成一棵樹,這樣的話,我們只要遍歷這組節點的所有可能賦值情況即可。
Conditioning: instantiate a variable, prune its neighbors' domains
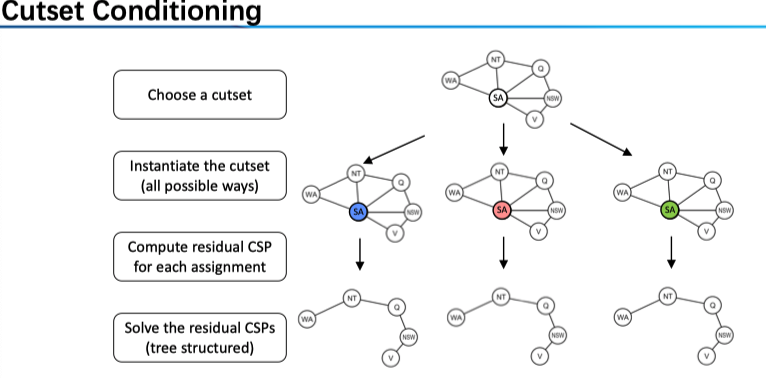
Cycle Cutset conditioning: instantiate (in all ways) a set of variables such that the remaining constraint graph is a tree.
所以我們的任務是找到這樣的 Cycle Cutset,若其大小為 c,則找到這個集合之后,搜索的時間復雜度為 \(O( (d^c ) (n-c) d^2)\)
Iterative Improvement
在上述 Backtracking 算法中,我們仍一個一個對變量進行賦值,但 CSP 只關心結果,因此一個自然的想法是直接從 complete state 出發,尋找解。Iterative Improvement 是一種 Local Search 方法。我們
- Take an assignment with unsatisfied constraints
- 然后 Operators reassign variable values。
具體來說,我們 1. Variable selection: randomly select any conflicted variable;2. Value selection: min-conflicts heuristic: Choose a value that violates the fewest constraints。這里第二步的變量選擇使得沖突最少的那一個,可以認為是一種 heuristic \(h(n)=\) #total number of violated constraints。
這里體現的是 Local Search versus Systematic Search,相較於 BFS, DFS, IDS, Best-First, A* 等系統搜索算法(Keeps some history of visited nodes)來說,后者的一大特點就是不保留 history,然而,這在減少了存儲負擔的情況帶來的問題則是失去了 complet 性質,容易陷入局部最優。
一些 Local Search 包括
- Hill climbing:在 neighbor 中找最優值,迭代,可能陷入局部最優
- Simulated annealing:結合了 random walk 和 hill climbing。在循環過程匯總,與 hill climbing 的不同在於,對於 next state 來說,若是較為「好的」則以概率 1 接受;若相較於前一個狀態變差了不是直接拒絕而是以一定的概率 \(P(T)\) 接受(random walk)。接受的概率隨着時間降低,也就是「模擬退火」的命名原因。具體的,接受概率為 T 的函數,如 \(\exp(\Delta E/T)\) 其中 \(\Delta E\) 可表為 next value - current value,而\(T\) 隨着時間而降低,即從 random walk 逐漸變為 hill climbing。
- Local beam search:並行 k 個 hill climbing——對於 Systematic search 來說保留所有的歷史,而前兩種僅保留一個,都太極端了,Local beam search 每次保留 k 個 complete state 而它們的 successor 中找最好的(加入了 randomness)的 k 個后代進行下一次模擬。
- Genetic algorithm
另,對於連續函數來說,則要采用梯度下降方法 Gradient decent。
進一步閱讀:《人工智能》chapter 4.1 – 4.2。
