極小連通子圖與極大連通子圖是在無向圖中進行討論的。
極大強連通子圖是在有向圖中進行討論的,不存在極小強連通子圖。
無向圖
連通圖:
在無向圖中,若從定點V1到V2有路徑,則稱頂點V1和V2是連通的。如果圖中任意一對頂點都是連通的,則稱此圖是連通圖。(連通的無向圖)
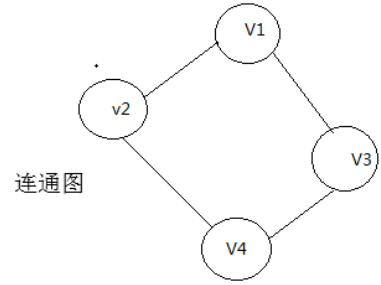
極大連通子圖:
1.連通圖只有一個極大連通子圖,就是它本身。(是唯一的)
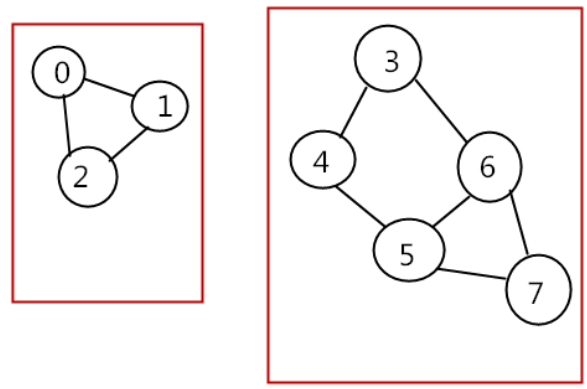
2.非連通圖有多個極大連通子圖。(非連通圖的極大連通子圖叫做連通分量,每個分量都是一個連通圖)
3.稱為極大是因為如果此時加入任何一個不在圖的點集中的點都會導致它不再連通。
下圖為非連通圖,圖中有兩個極大連通子圖(連通分量)。
極小連通子圖:
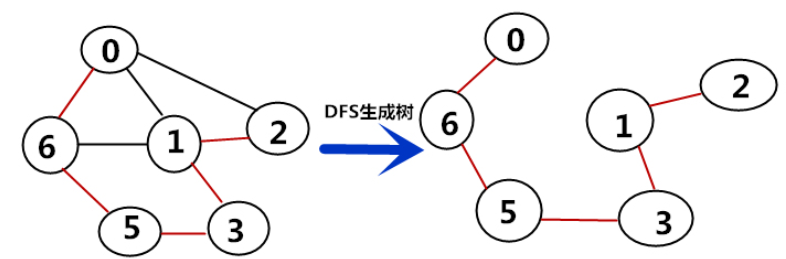
1.一個連通圖的生成樹是該連通圖的的極小連通子圖。(同一個連通圖可以有不同的生成樹,所以生成樹不是唯一的)
(極小連通子圖只存在於連通圖中)
2.用邊把極小連通子圖中所有節點給連起來,若有n個節點,則有n-1條邊。如下圖生成樹有6個節點,有5條邊。
3.之所以稱為極小是因為此時如果刪除一條邊,就無法構成生成樹,也就是說給極小連通子圖的每個邊都是不可少的。
4.如果在生成樹上添加一條邊,一定會構成一個環。
也就是說只要能連通圖的所有頂點而又不產生回路的任何子圖都是它的生成樹。
總結來說:極大連通子圖是討論連通分量的,極小連通子圖是討論生成樹的。
.
.
在這里順帶提一下強連通圖和極大強連通子圖。
強連通圖
強連通圖:
在有向圖中,若對於每一對頂點Vi和Vj,都存在一條從Vi到Vj和從Vj到Vi的路徑,則稱此圖為強連通圖。(連通的有向圖)
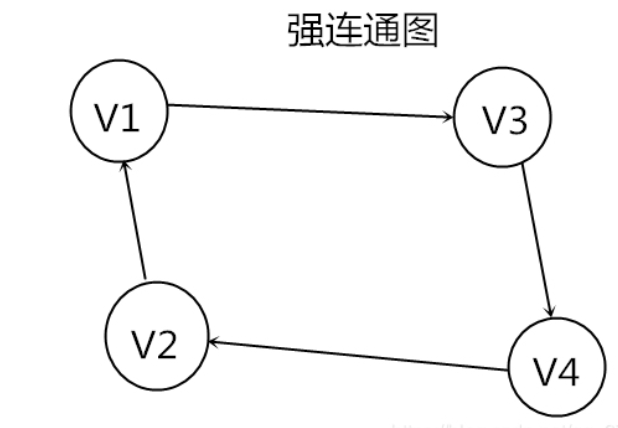
有n個頂點的強連通圖最多有n(n-1)條標,最少有n條邊。(4個頂點的強連通圖圖示如上圖和下圖)
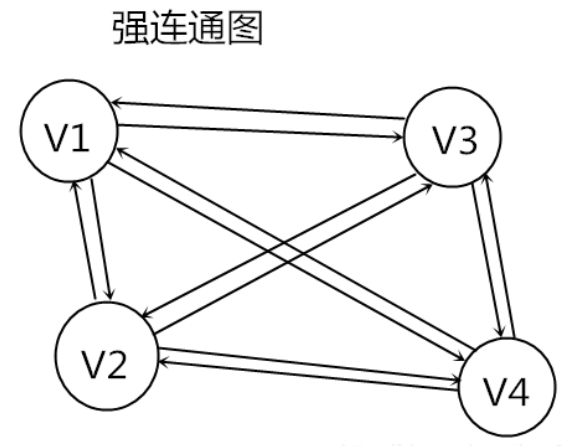
極大強連通子圖:
1.強連通圖的極大強連通子圖為其本身。(是唯一的)
2.非強連通圖有多個極大強連通子圖。(非強連通圖的極大強連通子圖叫做強連通分量)
極小強連通子圖:不存在這個概念
本文為CSDN博主「少博1557」的原創文章,遵循 CC 4.0 BY-SA 版權協議
