論文筆記（一）SecureML: A System for Scalable Privacy-Preserving Machine Learning

SecureML：A system for Scalable Privacy-Preserving Machine Learning

1 摘要及介紹

1.1　模型的大致架構

首先，主要模型中主要有客戶端和兩台服務器，假設這兩台服務器不會惡意合作。
　　整個訓練過程大致分為在線和離線兩個階段，在線階段的主要任務就是利用本文提出的安全算數技術在共享的十進制數上進行模型的更新，根據混淆電路的思想，除了最后能得到的模型，什么數據也不會暴露出來；離線階段的主要任務是服務於在線階段的乘法運算——利用線性同態加密或者不經意傳輸生成必要的三元組，因為這個開銷比較大，后期還提出了一種改進，用客戶端來輔助生成三元組；

1.２ 主要貢獻

• 為線性回歸、邏輯回歸、神經網絡這三種機器學習算法開發出了新型的隱私保護的深度學習協議
• 開發出了支持在共享的十進制數上的安全算數操作的技術
• 對於那些非線性激活函數，如sigmoid softmax，提出了一種支持安全多方計算的替代方案
• 以上提出的所有技術相較於目前的技術，在保證安全的前提下，速度上都有很大的提升

1.2.1 為三種機器學習算法開發出的隱私保護的協議

線性回歸、邏輯回歸和神經網絡這三種機器學習方案非常簡單但也非常常用，而且他們之間思想類似且一種遞進的趨勢。
所謂思想類似指的是他們都是有監督的機器學習算法，思路都是先前饋，算出交叉熵之后，在利用隨機梯度下降，再后饋更新模型。
所謂遞進指的是，線性回歸只涉及到了簡單的加乘操作，本質上講不考慮效率的情況下，只要能夠實現隱私保護的線性操作即可實現線性回歸，最簡單的混淆電路即可實現，但本文考慮了效率，所以提出了一種更快的在共享的十進制數上的安全算法操作技術。而邏輯回歸相較於線性回歸，只是多了激活函數，所以作者提出了一種替代的解決方案。而神經網絡在算法設計上雖然與邏輯回歸不同，但是其“組件”上依然是線性操作＋激活函數。

1.2.2. 更快的安全兩方乘法——在共享的十進制數上的算數操作

前人主要的性能瓶頸是在安全兩方計算，比如姚氏混淆電路中，計算定點乘法操作開銷非常大。

本文提出的方案：將這兩個共享的十進制數表示成有限域上的整數，使用離線生成的三元組在共享的整數上執行乘法操作，每一方都截斷它所擁有的積的那部分，因而固定數量的比特即可表示小數部分。經過驗證，即使是用截斷之后的share恢復出來的乘積，相較於定點乘法差距不大，誤差幾乎可以忽略不計。

1.2.3支持安全多方計算的激活函數

邏輯回歸和神經網絡必須使用sigmoid和softmax，但現在使用的用多項式去模擬激活函數的方式是低效。

本文提出了一種新的激活函數，類似於兩個RELU函數之和並用小型混淆電路求和，來替代sigmoid，並用到了在算數分享和姚氏分享之間的切換。與之類似，為了替代softmax，提出了一種結合了RELU、加法和除法結合的激活函數。

1.2.4 其他提高效率的方法——向量化與客戶端輔助生成三元組

​ 為了提高系統的整體效率，還提出了提高整體性能的方法，如向量化，提取數量數據的時候按batch來提取。離線階段，提出一種更快的、每個客戶幫助產生三元組的離線階段。但是比起標准設定，安全性保證不夠好，因為它需要客戶端和服務器不會同流合污。

2 基礎知識

2.1 機器學習

因為本文的重點在於隱私保護，所以涉及到的機器學習三個算法都是非常基礎的，是機器學習中的"hello world"級的線性回歸、邏輯回歸和神經網絡這三個算法。而且整體思路也幾乎相同——先前饋，求出交叉熵，然后使用隨機梯度下降再后饋來更新模型。以下是對於他們的簡單回顧：

2.1.1　線性回歸

線性回歸是根據現有點，擬合出一個n元一次函數，所謂的模型就是系數向量w，把數據向量化表示之后，更新模型最核心的公式是：
$$
w:=w-{1\over |B|}\alpha X^T_B×(X_B×w-Y_B)
$$
其中，w為系數矩陣，也就是所謂的“模型”，每次訓練時選出的那組數據叫做一個batch，|B|就是batch中數據的個數，(XB,YB)就是一個batch中所有的數據組成的向量組，物理意義其實就是函數圖像上的很多點。

2.1.2　邏輯回歸

邏輯回歸在二分類問題上很常用，它一般得到的是一個介於0~1之間的數。邏輯回歸和線性回歸很類似，但是多了一個激活函數，就是這個激活函數使整個算法從線性飛躍到了非線性，把數據向量化之后，更新模型的公式和線性回歸也很像，就是多了激活函數f：
$$
w:=w-{1\over {|B|}}\alpha X^T_B×(f(X_B×w)-Y_B)
$$
各個符號的意義和線性回歸的幾乎一樣，激活函數f一般要么是logistic（這篇文章里叫logistic，但我看一般的機器學習資料里管他叫sigmoid）：
$$
y={1\over {1+e^{-x}}}
$$
或者是softmax:
$$
y = {e^{-x_i} \over \sum e^{-x_i}}
$$
這都是很常見的激活函數了。

2.1.3　神經網絡

這里提出的神經網絡也是最常見的BP神經網絡，整個過程和線性回歸和邏輯回歸大同小異。從本質上來說，線性回歸只涉及到了線性的加乘操作，邏輯回歸多了激活函數，神經網絡相較於前兩種算法在這個方面並沒有什么本質上的突破，所以只要解決了線性和激活函數的隱私計算問題，這三種機器學習算法的運算問題都得到了解決。

作為深度學習的“hello world”任務，MNIST是所有新手的第一關，任務也非常簡單，就是分類任務，不過是多分類。思路也類似，所謂的“模型”就是每一層神經網絡之間的系數矩陣，先前饋，求出交叉熵，然后隨機梯度下降，再后饋調整系數矩陣，最終達到一個比較理想的結果：
$$
W_i := W_i - {\alpha\over|B|}×f(X_{i-1}×W_i)×Y_i
$$

2.2 安全計算

2.2.1 不經意傳輸

​ 不經意傳輸是安全多方計算常用的技術：有一個發送者S,他有兩個輸入x0和x1，又有一個接收者R,它有一個選擇比特b，得到xb（b∈{0,1}），但是S不知道b究竟是什么，而R也不可能知道除xb之外的另一個輸入是什么。符號描述起來是：(null, xb) <- OT(x0,x1;xb)，偽代碼描述起來是這樣：

Parameter: Sender S and Receiver R

Main: On input (SELECT, sid, d) from R and (SEND, sid, x0, x1) from S, return (RECV, sid, xb) to R.

（：P8不經意傳輸的算法描述

我們在兩個地方使用使用不經意傳輸：1、離線階段產生三元組 2、計算激活函數

傳統的不經意傳輸效率較低，這里使用了一種擴展的不經意傳輸correlated OT擴展，記作COT，能夠允許接收和發送者執行m個OTs以n(n，一個安全參數)基、帶有公鑰操作的OTs和O(m)快速對稱密鑰操作的代價。在這里，兩個輸入是不獨立的，s0是一個隨機數，而s1=f(s0)，f是用戶選定的一個系數矩陣。一個l-bit消息的COT，記作COTL，是n+l比特，計算由三個哈希組成。

2.2.2 混淆電路兩方安全計算

混淆電路的目的是為了根據兩方的輸入x,y計算出f(x,y)的結果，但是參與運算的彼此不可能知道對方的輸入，一套混淆方案大致由一下幾部分組成：

	參數１	參數2	輸出１	輸出２
混淆算法	隨機種子$	函數f	混淆電路F	解碼表dec
解碼表dec	隨機種子$	x	混淆輸入x^
評價(evaluation)算法	混淆輸入x^	混淆電路FZ[i] = UBi* V[i]	混淆輸出z^
解碼算法	混淆輸出z^	解碼表dec	f(x)

給定上述方案，則可以設計出一套安全兩方計算協議，在一般的類似協議中，alice叫做generator，bob叫做evaluator。generator負責自己設計密鑰，把整個真值表加密、混淆，然后和evluator利用不經意傳輸協議，evaluator做出選擇之后，將選中的label和他的密鑰還給evalator，兩方再分別解密。一個例子如下:

1. alice運行混淆算法：根據隨機種子和函數f,生成混淆電路GC和解碼表dec

2. alice將x放入解碼表dec編碼之后得到混淆輸入x^

3. alice將混淆電路GC和混淆輸入x^發送給bob

4. bob通過不經意傳輸，得到了自己的混淆輸入y^

5. bob接着在GC上執行評價算法——通過x^ y^{和混淆電路GC得到混淆輸出z}

6. 雙方通過解碼算法得到最終結果f(x)

   以上算法被記作：(za,zb) <- GarbledCircut(x;y,f)

2.2.3　秘密分享和三元組

​ 在我們的協議中，所有的中間結果都被兩個服務器所秘密分享的。這里實現了三種不同的分享方案：加法、布爾和乘法分享。

一、加法分享

　　所謂將a加法分享，就是將a拆成兩個數字，這兩個數字之和是a，這兩個數字由兩方分別保存。記作(ShrA(.))。為了加法分享一個l-bit的值a，記作<.>，以alice和bob為例：

1. alice隨機產生一個2^l范圍內的整數a0 (a0記作<a>A0 )

2. alice計算出a1 = a - a0 mod 2^l

3. alice將a1發送給bob (a1記作<a>A1)

   為了恢復RecA(.,.)已經被加法分享的值a，Pi將<a>i發送給P1-i，雙方分別計算<a>0+<a>1

二、乘法分享

​ 所謂將c乘法分享，就是將c拆成兩個數字，而這兩個數字之積是c，這兩個數字由兩方分別保存。記作(MulA(.,.))。現在c已經被分享成了<a>和<b>，我們假設雙方已經共享了<u> <v> <z>，其中：

• u和v都是2^l整數域內的隨機值

• z = u*v mod 2^l

  乘法分享流程如下：

1. Pi本地計算<e>i = <a>i - <u>i
2. Pi本地計算<f>i = <b>i - <v>i
3. Pi運行Rec(<e>0, <e>1)
4. Pi運行Rec(<f>0, <f>1)
5. Pi計算

$$
c_i = -i * e * f + f * _i + e * _i + _i
$$

三、布爾分享

布爾分享可以被視作在{0,1}整數域內的加法分享，其中異或被加法替代，邏輯與被乘法替代。
　　關於布爾分享和姚氏分享：此協議中不顯式使用姚氏分享，因為它會被隱藏在混淆方案中，但是Y2B轉換會被使用來將混淆輸出變成布爾分享
　　可以把混淆電路協議視作操作姚氏分享的輸入來產生姚氏分享的輸出。特別地，在所有混淆方案中，generator為每個wire w產生兩個隨機字符串kw0,kw1。當使用點＆排序技術時，generator也產生隨機排序比特rw，使Kw0 = kw0||rw，Kw1 = kw1 || (1-rw)。被排成串的比特流一會被用來排序每個被混淆真值表的行
　　比如，數字a的姚氏分享是<a>Y0 = Kw0, Kw1 & <a>Y1 = Kwa。為了恢復被分享的值，參與者交換他們的shares，異或或者邏輯與會被執行來評價相關的邏輯門。
　　從姚氏分享切換到布爾分享的操作記作Y2B(.,.)，其中，姚氏分享<a>Y0 = Kw0, Kw1 & <a>Y1 = Kwa，布爾分享則變成了P0擁有<a>B0＝Kw0[0]，P1擁有<a>B1= <a>Y1[0]=Kwa[0]換句話說，混淆方案中用來排序的比特可以被無縫切換到布爾分享。

3 隱私保護的機器學習

3.1　隱私保護的線性回歸

​ 基於算數秘密分享和三元組的隱私保護的線性回歸

訓練數據被秘密分享於兩個服務器S0 S1上，我們將其分別記為(<X>0, <Y>0) (<X>1, <Y>1)。s0可以使用它的公鑰來加密第一個share，然后將加密后的結果和明文share上傳S1上，S1把被加密的share傳給S0來解密。

數據被秘密分享，模型也被秘密分享——系數矩陣w也被秘密分享於兩個服務器上，初始階段都是隨機值，在兩個服務器之間沒有任何通信。每一輪GSD之后，它被更新但仍然保持秘密分享，直到訓練的最后才會恢復。

在線階段，我們進行線性回歸的更新，公式是：
$$
w_j := w_j - \alpha(\sum^d_{k=1}x_{ik}w_k-y_i)x_{ij}
$$
因為沒有向量化，所以這是一個個的數字，根據之前所述，這些數字都是被秘密分享在兩個服務器上的，又因為只有加法和乘法，因此我們使用相應的、被分享值的加法和乘法算法給來更新系數：
$$
<w_j>　:= <w_j> - \alpha Mul^A(\sumd_{k=1}Mul ^A(<x_{ik}>,<w_k>)-<y_i>,<x_{ij}>)
$$
也就是說每個服務器用這個公式來分別更新自己本地的相應的值。

3.1.1　向量化

上面那個只是針對一個訓練數據，舉個例子，比如d=3，有這樣一個訓練數據([x1 x2 x3], y[1])，更新時就是i=1,j從1到3.

我們想要同時訓練一個batch的數據，這樣可以提高效率，所以可以使用向量化技術。所以我們將共享值上的線性操作推廣到了共享矩陣上的線性操作。其實非常類似，就是把所有的值都換成了矩陣即可，矩陣中的每個元素視作共享值即可。如果mini-batch有B條數據，那么在線階段的更新公式就是變成了：
$$
<\bold w> := <\bold w> - {1\over|\bold B| } \alpha Mul^A(<\bold X^T_B>,MulA(<\bold X_B>,<\bold w>)-<\bold Y_B>)
$$
一個樣本在不同的輪次上會被使用很多次，它滿足用同樣的隨機三元組來掩蓋它。因此離線階段，一個共享的n*d隨機矩陣<U>被用來生成掩蓋數據樣本<X>。

在線階段的起始階段，<E>i = <X>i - <Y>i被計算並被交換來重構E。此后，EB被選擇而且被使用在乘法協議中，不帶有任何更多的計算和交流。特別的，在離線階段，一系列下標B1,B2...Bt在兩個服務器間得到公認。僅僅需要n,d,t的知識或者一個上標而不需要真實數據。然后三元組<U>,<V>,<Z>,<V'>,<Z'>被提前計算：

	維度	作用	備注
U	n×d	mask data X
V	d×t	每一列用來mask w	forward propagation
Z	|B|×t	中間結果	Z[i] = UBi* V[i]
V'	|B|×t	每一列用來mask Y* - Y	backward propagation
Z'	d×t	中間結果	Z'[i] = UTBi* V'[i]

將數據用矩陣形式表示，將大大降低交流和通信的效率.

3.1.2　被分享的十進制數上的算數操作

正如之前討論的，前人工作的不高效主要來源於在共享/加密的十進制數上的計算，之前的解決方案主要有兩種：
1、把共享的十進制數看成整數，做乘法后在很大的有限域上完全保留下所有的精度。缺點是只能支持一定數量的乘法，因為結果的范圍會隨着乘法的數量指數級增長。
２、在十進制數上利用安全兩方計算的布爾電路來做定點或者浮點乘法。這帶來了大量的負載，因為計算兩個l-比特長的數的乘法就需要O(l^2)個門，在2PC（例如姚氏混淆電路中），這樣的電路需要為每個乘法進都算一次。

本文提出了一種簡單但有效的支持有限域上的十進制數的解決方案。考慮對兩個小數部分最多有lD比特的兩個十進制數x y的定點乘法，首先把通過x' = 2^lD×x,y' = 2^lD×y，把數字轉化成整數，然后把他們相乘得到z = x'×y'，注意到z最多有2lD表示積的小數部分，所以我們簡單粗暴地將最后z的最后lD比特砍掉，這樣它最多有lD比特來表示小數部分。
z也可以被秘密分享，可以證明，兩個服務器分別砍去自己的最后lD位比特，和想要的z其實最多相差一個最不重要的比特位，這對最后結果的影響可以說是微乎其微。換句話說，相較於標准的定點乘，我們只是缺少了小數部分最不重要的一個比特位。

隱私保護的線性回歸的在線部分的協議如圖所示：

協議假定了數據無關的共享矩陣<U><V><Z><V'><Z'>已經在離線階段產生，除了共享十進制數的加乘，協議還需要將系數向量和學習率相乘，為了讓乘法更有效率，將{\alpha \over |B|}變成2的冪次，比如{\alpha \over |B|} = 2^{-k}

3.2　離線階段——產生三元組子

說到底我還是不理解，在線和離線階段都分別用來干什么？我的理解是，所謂模型更新，所需要的不過是一次線性混淆計算，簡單來講，就是雙方共同計算一個a*b即可，然后各自可以得到計算結果。這么講吧，你自己也發現了，你自己其實可能根本不需要online就能做很多事情，你所需要online做的只是一小部分，很多事情沒必要online做了，所以分成了online和offline。

那我們這里線下做了些什么呢？就是generate 三元組。對啊，我就是想問，為什么offline的一定是generate 三元組？而不是其他的工作？

回憶一下，給定共享隨機矩陣（這里所謂的共享是什么意思？是兩方擁有一樣的矩陣？還是說這個矩陣被秘密分享，即可以用兩個數字相加恢復出來？）<U>，<V>關鍵步驟是從<U>中選擇一個|B|×d的子矩陣，和從<V>選擇一個列並計算他們積的shares，這被重復t次來計算出<Z>,<Z'>被這樣計算以相反的維度。

因此，簡化起見，我們關於於基礎步驟，給定|B|×d的矩陣<A>的shares，和一個d×1的矩陣<B>的shares，我們想要計算|B|×1的矩陣<C>的shares。我們利用接下來的關系：C = <A>0 ×<B>0 + <A>0 ×<B>1 +<A>1 ×<B>0 +<A>1 ×<B>1。<<A>0 ×<B>1> <<A>1 ×<B>0>可以合作計算，而 <A>0 ×<B>0 <A>1 ×<B>1即可在本地計算。

接下來就是如何合作計算<<A>0 ×<B>1> 、<<A>1 ×<B>0>>這兩個式子的問題

3.2.1　基於同態加密的生成

為了計算<A>0 ×<B>1的shares，S1使用LHE加密<B>1的每個元素，並將它發送給S0。S0然后在密文上執行矩陣乘法，其中加法被乘法替代，乘法被冪運算取代。最后，S0將得到的密文用隨機值掩蓋，發送給S1解密。最終的結果就是S0和S1分別得到了<<A>0 ×<B>1>0和<<A>0 ×<B>1>1這兩個shares。對於計算<<A>1 ×<B>0>>，方法是一樣的。再用上可以本地計算的兩個式子，C即可算出出來。說白了，線下階段就是在計算無法本地計算的三元組子嘛？

我大概懂了什么叫generate 三元組，說白了就是根據本地存儲的<A>和<B>計算出<C>，上面的分析是將求出<C>拆成四個式子的運算，一半可以offline做，一半需要交流。需要交流的那個兩個式子的求解過程只需要傳送一下兩個被加密/混淆過的矩陣即可，通信開銷小。計算開銷通過分析是可以接受的.

3.2.2　基於不經意傳輸的生成

上面的問題——計算<<A>0 ×<B>1>的shares也可以用不經意傳輸來解決，步驟如下：

1. S1使用bj個比特來選擇從2個使用COT從aij中計算出來的值選一個出來（明明就是一個aij，為什么要變成兩個，而且怎么變成兩個的？？？）
2. 對於k=1~l，S0設置COT的系數函數為fk(x)=aij*2^k+x mod 2^l
3. S0執行COT(rk,fk(xj); bj[k])
4. S1執行COT(rk, fk(x); bj[k])
   • 如果bj[k] = 0，S1得到　rk
   • 如果bj[k] = 1，S1得到　aij*2^k+x mod 2^l
   • 也可以寫成bj[k] * aij * 2^k + rk mod 2^l

$$
<a_{ij},b_j>_0 = \sum _{k=1}^l*(-r_k) (mod 2^l)
$$

$$
<a_{ij},b_j> 1= \sum {k=1}^{l(b_j[k]*aij*2}k+r_k)= a{ij}*b_j+\sum{k=1}^lr_k (mod 2^l)
$$

3.3　隱私保護的邏輯回歸

相較於線性回歸，邏輯回歸需要在共享數字上計算激活函數：
$$
f(u)={1\over 1+e^{-u}}
$$
這其中有除法有冪運算，很難用算數或布爾電路來進行安全兩方計算。之前使用的用多項式去近似的方法雖然可以行但是效率太低而無法使用。

3.3.1　安全計算友好型激活函數

所以作者提出用這樣一種激活函數來作為替代方案：

$$
f(x)=\begin{cases}0,&if \quad x<-{1\over 2}\cr x+{1\over 2},&if \quad -{1\over 2} \leq x \leq {1\over 2}\cr1,&if\quad x> {1\over 2} \end{cases}
$$

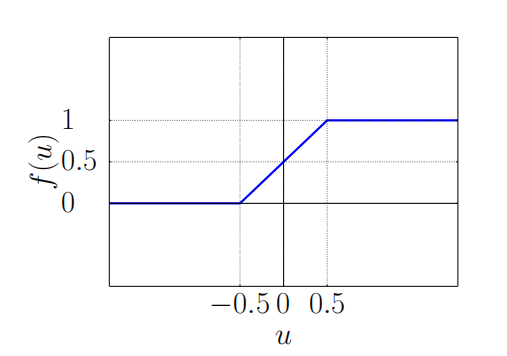
之所以使用這個函數，一來是因為它在邊界很容易收斂到0或1，而且和RELU函數很像。

一旦我們使用新的激活函數，在計算后饋階段時，我們使用相同的更新函數作為邏輯函數，即繼續使用邏輯函數計算偏導數，這種方法經過實驗證明效率很好。作者頁建議探索更多安全多方計算友好型可以被簡單的布爾和算數電路計算的激活函數。

3.3.2　隱私保護協議

新的激活函數是電路友好型。它僅僅包含了測試輸入是否在[-1/2,1/2]這個區間。但是，僅僅把姚氏混淆電路協議整個的直接用到激活函數中是不高效的。相反，我們利用在算數分享和姚氏分享之間切換的技術。邏輯回歸和線性回歸隨機梯度下降的唯一不同就是邏輯回歸在每個前饋過程都多了一個額外的激活函數。因此，首先我們和計算線性回歸一樣，先計算除了數據和系數矩陣的內積，然后將算數分享切換到姚氏分享並計算激活函數的值使用混淆電路。然后在切換回算數分享來繼續后饋過程。具體訓練過程如下：

3.4　隱私保護的神經網絡訓練

在隱私保護的線性回歸和邏輯回歸都可以被很順暢地擴展來支持隱私保護的神經網絡的訓練，我可以使用RELU函數作為每個神經元的激活函數，交叉熵作為損失函數。每個神經元的系數的更新函數都可以像表達成像2.1中討論的那種封閉模式。除了激活函數的求值和偏導函數外，前饋和后饋階段的所有函數都是簡單的線性操作。為了給RELU函數求和和求導，我們像給邏輯函數那樣轉換到姚氏分享即可，混淆電路僅僅將兩個shares相加並輸出最重要的比特，比我們在邏輯函數中使用的電路還要簡單。RELU的求值和求導函數可以在一輪之內一起求出來，求導的結果用在后饋階段。
　　我們也提出了安全多方計算友好型的softmax的替代方案。然后我們將RELU所有的輸出加起來求和，使用出發電路，將每個輸出除以總和。這樣，輸出可以保證是概率分布。
　　根據實驗中的觀察，花在RELU混淆電路上的時間占了大量的在線訓練時間。因此，我們也考慮將激活函數替換成平方函數。這樣調整之后，我們達到了93.1%的准確率。現在，一個計算RELU函數的混淆電路被在共享值上的三元組子所替代，在線階段的性能大大提高。但是，這種方法花費了更多的三元組也提高了在線階段的開銷。

3.4.1　效率討論

在線階段，計算復雜度是　使用矩陣算數操作的明文訓練加上RELU求值和使用混淆電路和不經意傳輸的　兩倍。
離線階段，三元組的總數相較於增長了O(\sum^m_{i=1}d_m)相較於回歸，這其實是神經元的總數。一些三元組子可以為在線矩陣乘法以矩陣形式產生

3.5.1　隱私保護預測

我們迭代我們可以隱藏輸入數據、模型、預測結果和他們的任意組合，因為在我們的協議中他們可以秘密分享。如果要么輸入數據、要么模型可以被揭露出來，效率可以進一步提升，例如，如果模型是明文，帶有矩陣的輸入數據的乘法可以被直接計算在shares，不需要直接計算的三元組

4 客戶端輔助的離線協議

主要的性能瓶頸是離線階段，它包含大量的密碼學操作例如OT或者LHE，，當然會比在線階段的在有限域上的簡單的加乘操作慢。這刺激我們去尋找另外一種產生三元組的替代方案。尤其，我們讓客戶端產生三元組。既然客戶端首先需要秘密分享他們的數據，進一步讓他們秘密分享一些額外的三元組也是自然而然的事情。現在，一些三元組可以在沒有任何秘密學操作、以可信任的方式產生。這大大提高了效率，盡管他有好處，也改變了安全模型。

4.1　客戶端輔助的三元組

簡單起見，注意到在整個訓練過程中，每個數據樣本中的特征在兩個三元組子中用到了——一次是在前饋階段，一次是在后饋階段。因此，它suffices for客戶端持有這個值來產生2E三元組。尤其，對於每個樣本中的每個特征，客戶端處理數據來產生隨機值u來掩蓋數據，產生隨機值vk，vk'　for k = 1~E並計算zk=u*vk，zk'=u* vk'　最后，客戶端將<u>, <vk>, <vk'>, <zk>, <zk'>的shares分布在兩個服務器上。這次操作我肯定在哪里見過，如果是服務器做，該怎么做呢？服

我們不假定客戶端在產生三元組的時候知道數據是如何partitioning的，這意味着我們無法從在線階段的向量化中獲益。舉個例子，在線性回歸的前饋階段，我們使用之前計算的和在線階段具有一樣的維度的矩陣三元組U×V=Z。現在，當三元組被客戶端產生時，在mini-batch Xb中的數據或許屬於不同的，且不知道他們擁有相同的訓練batch的客戶端，因此不同共認一個共同的隨機矩陣V來計算Z
相反的，如果不進行向量化，即對於在XB中的每個數據樣本x,雙方使用獨立產生的三元組計算<y*>=MulA(<x,w))。因此，在線階段的通信、計算開銷和兩台服務器的存儲負載都提高了。
客戶端輔助三元組產生因為沒有密碼學操作參與其中，雖然提高了離線階段的效率，但是因為矩陣三元組被向量的內積所替代，它將負載引入了在線階段。所要執行的乘法的總數是相同的，總體上，矩陣相乘算法比使用編程語言中的矩陣庫要快。這是最大的被客戶端輔助產生三元組引入的負載。
通信的開銷也同樣上升了，以前系數矩陣被一個隨機矩陣所掩蓋來計算一個矩陣乘法，現在每計算一個內積就要被很多不同的隨機矩陣來掩蓋。被掩蓋的值要用安全計算協議在兩方之間傳輸。
　　最后，存儲開銷也提升了。先前，矩陣V和矩陣Z比數據大小要遠遠地小，矩陣U和數據一樣的大小。現在，因為三元組子被獨立產生，V的大小變成了|B|*d*t=n*d*E，比數據的大小要多出一個E。U的大小仍然一樣，因為每個數據仍然被一個隨機值所掩蓋，Z的大小仍然相同因為一旦服務器從所有的客戶端那里收到了shares，值將會被聚合。
　　盡管有這樣負載，因為離線階段被大大提升，在線階段仍然是有效率的，所以整體的性能被大大提升。這種客戶端輔助產生三元組的架構也是是現在最有前景的一種架構。

4.2　新的安全模型

安全模型也隨之發生改變，僅僅記下改變的那一部分。先前，用戶只負責上傳數據，因此服務器當然無法知道任何信息當它和一小部分客戶端同流合污時。現在，因為客戶端也產生三元組，如果一小部分客戶端和服務器聯合起來時，他們或許可以恢復出系數矩陣，這損害了誠實客戶端的利益。因此在這個安全模型中不允許服務器和客戶端同流合污。