學號 2019-2020-20182321 《數據結構與面向對象程序設計》第八周學習總結
教材學習內容總結
- 樹與前面的棧、隊列還有鏈表不同,樹是一個非線性集合。
- 樹的構成元素有邊和節點,節點里儲存着樹的內容,邊是各個節點之間的連接,可以讓我們從樹的一個節點訪問到另一個節點。
- 樹(英語:tree)是一種抽象數據類型或是實現這種抽象數據類型的數據結構,用來模擬具有樹狀結構性質的數據集合。它是由n(n>0)個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的
- 樹有以下的特點:
①每個節點有零個或多個子節點;
②沒有父節點的節點稱為根節點;
③每一個非根節點有且只有一個父節點;
④除了根節點外,每個子節點可以分為多個不相交的子樹;
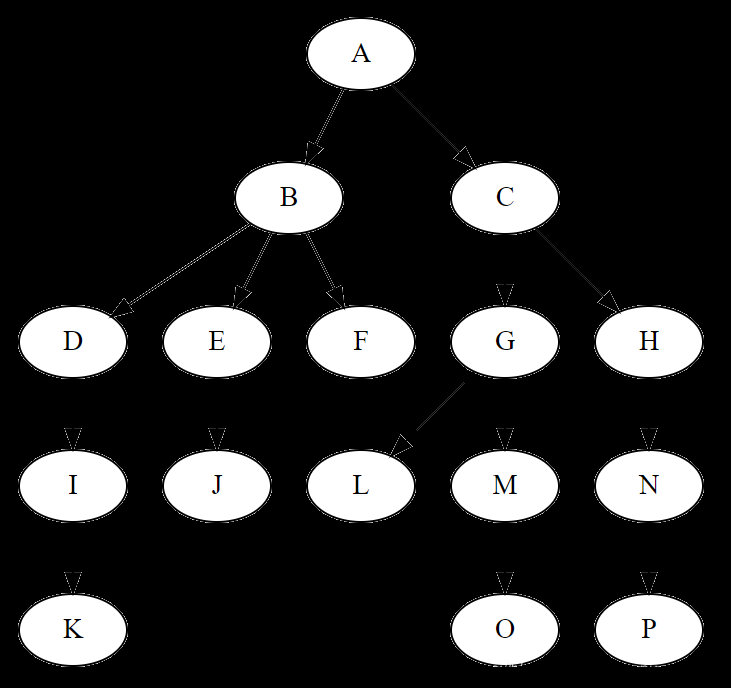
- 實現樹的方法有數組和鏈表兩個方法,數組是運用了父親節點和其子節點之間的序號關系來進行構建數,而鏈表方法其實只是在一個節點中增加多個引用,使其可以擴展、分支。
- 數的遍歷方法有中序遍歷、前序遍歷、后序遍歷三種
- 運用二叉樹表示決策樹,其實只是在每個二叉樹的節點里存儲一個字符換元素,然后根據決策者的Yes或者no來進行決策。
- 二叉查找樹的一個特性是,比其節點小的數會再節點的左子樹處,比節點大的數 會在節點的右子數處
- 樹的基本術語:
節點的度:節點擁有的子樹的數目。
葉子:度為零的節點。
分支節點:度不為零的節點。
樹的度:樹中節點的最大的度。
層次:根節點的層次為1,其余節點的層次等於該節點的雙親的層次加1。
樹的高度:樹中節點的最大層次。
無序樹:如果樹中節點的各子樹之間的次序是不重要的,可以交換位置。
有序樹:如果樹中節點的各子樹之間的次序是重要的,不可以交換位置。
森林:0個或多個不相交的樹組成。對森林加上一個根,森林就成了樹。刪去根,樹就成了森林。
- 除了二叉查找樹還有滿二叉樹以及完全二叉樹
- 平衡二叉搜索樹(英語:Balanced Binary Tree)是一種結構平衡的二叉搜索樹,即葉節點高度差的絕對值不超過1,並且左右兩個子樹都是一棵平衡二叉樹
-二叉查找樹還有可以左旋轉和右-左旋轉、左-右旋轉、右旋轉。 具體如下圖




教材中遇到的問題和解決過程
- 問題1:什么是前序遍歷、中序遍歷、后序遍歷
- 問題1解決方法:
1.前序遍歷首先訪問根結點然后遍歷左子樹,最后遍歷右子樹。在遍歷左、右子樹時,仍然先訪問根結點,然后遍歷左子樹,最后遍歷右子樹。
若二叉樹為空則結束返回,否則:
(1)訪問根結點。
(2)前序遍歷左子樹。
(3)前序遍歷右子樹 。前序遍歷前序遍歷
需要注意的是:遍歷左右子樹時仍然采用前序遍歷方法。
如下圖

前序遍歷結果:ABDECF(我們在知道后序遍歷和中序遍歷的結果時也可以知道前序遍歷)
2.中序遍歷(LDR)是二叉樹遍歷的一種,也叫做中根遍歷、中序周游。在二叉樹中,先左后根再右。巧記:左根右。
中序遍歷首先遍歷左子樹,然后訪問根結點,最后遍歷右子樹若二叉樹為空則結束返回,
否則:
(1)中序遍歷左子樹
(2)訪問根結點
(3)中序遍歷右子樹
如下圖

中序遍歷結果:DBEAFC
3.后序遍歷(LRD)是二叉樹遍歷的一種,也叫做后根遍歷、后序周游,可記做左右根。后序遍歷有遞歸算法和非遞歸算法兩種。在二叉樹中,先左后右再根。巧記:左右根。
后序遍歷首先遍歷左子樹,然后遍歷右子樹,最后訪問根結點,在遍歷左、右子樹時,仍然先遍歷左子樹,然后遍歷右子樹,最后遍歷根結點。即:
若二叉樹為空則結束返回,
否則:
(1)后序遍歷左子樹
(2)后序遍歷右子樹
(3)訪問根結點
如下圖

后序遍歷結果:DEBFCA(已知前序遍歷和中序遍歷,就能確定后序遍歷。)
- 問題2:滿二叉樹和完全二叉樹的區別
- 問題2解決方法:
1.滿二叉樹定義:高度為h,並且有2^h-1個節點的二叉樹,叫做滿二叉樹。

2.完全二叉樹定義:二叉樹中,只有最下面兩層節點的度可以小於2,並且最下一層的葉節點集中在靠左的若干位置上,這樣的二叉樹稱之為完全二叉樹。
二叉樹中,只有最下面兩層節點的度可以小於2,並且最下一層的葉節點集中在靠左的若干位置上,這樣的二叉樹稱之為完全二叉樹。

通過上面我們可以觀察到,兩個二叉樹不同點就是在最后一行的節點處不同,滿二叉樹是每個節點都滿的,而完全二叉樹不一定。
- 問題3:何為決策樹?
- 問題3解決方法:決策樹(Decision Tree)是在已知各種情況發生概率的基礎上,通過構成決策樹來求取凈現值的期望值大於等於零的概率,評價項目風險,判斷其可行性的決策分析方法,是直觀運用概率分析的一種圖解法。由於這種決策分支畫成圖形很像一棵樹的枝干,故稱決策樹。
如下圖(摘自教材)

代碼調試中的問題和解決過程
- 問題1:如何用代碼實現前序遍歷、中序遍歷、后序遍歷
- 問題1解決方法:根據上面給我們的偽代碼思路,我們可以打出下面的前中后序遍歷方法代碼
前序遍歷
public static node creat(node node,String[] s1){
String temp = s1[i++];
if(temp.equals("#")){
return null;
}else{
node = new node(temp);
node.leftchild = creat(node.leftchild,s1);
node.rightchild = creat(node.rightchild,s1);
}
return node;
}
public static void first(node biTree)
{
Stack<node> stack = new Stack<node>();
while(biTree != null || !stack.isEmpty())
{
while(biTree != null)
{
System.out.println(biTree.data+" (前序非遞歸實現)");
stack.push(biTree);
biTree = biTree.leftchild;
}
if(!stack.isEmpty())
{
biTree = stack.pop();
biTree = biTree.rightchild;
}
}
運行結果為

中序遍歷
public static node creat(node node,String[] s1){
String temp = s1[i++];
if(temp.equals("#")){
return null;
}else{
node = new node(temp);
node.leftchild = creat(node.leftchild,s1);
node.rightchild = creat(node.rightchild,s1);
}
return node;
}
public static void midRe(node biTree)
{
if(biTree == null)
return;
else
{
midRe(biTree.leftchild);
System.out.println(biTree.data+" (中序遞歸)");
midRe(biTree.rightchild);
}
}

后序遍歷
public static node creat(node node,String[] s1){
String temp = s1[i++];
if(temp.equals("#")){
return null;
}else{
node = new node(temp);
node.leftchild = creat(node.leftchild,s1);
node.rightchild = creat(node.rightchild,s1);
}
return node;
}
public static void back(node biTree)
{
if(biTree == null)
return;
else
{
back(biTree.leftchild);
back(biTree.rightchild);
System.out.println(biTree.data+" (后序遍歷)");
}
}
運行結果

- 問題2:如何層序遍歷輸出二叉樹
- 問題2解決方法:
這里我想到的是利用數組來將二叉樹層序輸出。
如下圖

按照二叉樹的節點序號的規律,將二叉樹節點內的值賦值給數組,一個節點的左子樹是它的序號2i+1,它的右子樹是它的2i+2,賦值好了以后再一次性將其全部輸出就行了。下面是我的一部分代碼
String s = "A B # C D # # # E # F # #";
String[] a =s.split("\\s");
node root = new node();
root = creat(root,a);
node[] tree = new node[15];
tree[0] = root;
for(int i=1;i<tree.length;i++)
{
tree[i] = new node("#");
}
for(int i =0;i<15;i++)
{
if(i<15&&tree[i].leftchild!=null)
tree[i*2+1]=tree[i].leftchild;
if(i<15&&tree[i].rightchild!=null)
tree[i*2+2]=tree[i].rightchild;
}
代碼托管

(statistics.sh腳本的運行結果截圖)
上周考試錯題總結
- 錯題:In removing an element from a binary search tree, another node must be ___________ to replace the node being removed.
A.duplicated
B.demoted
C.promoted
D.None of the above
解析:覆蓋刪除節點的節點必須是前驅節點,這里是我的疏忽大意。正確選C。
2. 錯題:A binary search tree is a binary tree with the added property that the left child is greater than the parent, which is less than or equal to the right child.
A.True
B.Flase
解析:右邊的子樹一定要小於右邊的子樹,這題是看錯了
3. In removing an element from a binary search tree, another node must be demoted to replace the node being removed.
A.True
B.Flase
解析:不一定,刪除的情況有三種,所以這句話是錯的。
- To maintain the completeness of the tree, there is only one valid element to replace the root, and that is the element stored in the first leaf in the tree.
A.True
B.Flase
解析:不一定是樹的第一個葉子中的元素,應該是其前驅節點。
- 上周博客互評情況
- 20182334
- 結對照片

其他(感悟、思考等,可選)
其實我也不知道這周為什么我的代碼會突然激增那么多........但是學習二叉樹屬實讓我費力了不少,還會經常出現節點的左右樹枝被砍斷的情況,只能一步一步的debug來調整。
| 代碼行數(新增/累積) | 博客量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 623/1000 | 3/7 | 22/60 | |
| 第四周 | 600/1600 | 2/9 | 22/82 | |
| 第五周 | 1552/2987 | 2/11 | 22/94 | |
| 第六周 | 892/3879 | 2/11 | 22/114 | |
| 第七周 | 2284/6163 | 2/13 | 22/134 | |
| 第八周 | 2284/6163 | 2/13 | 22/134 | |
| 第九周 | 24118/30281 | 3/16 | 40/174 |
-
計划學習時間:10小時
-
實際學習時間:40小時
-
改進情況:
(有空多看看現代軟件工程 課件
軟件工程師能力自我評價表)
