最近在做一個深度學習分類項目,想看看訓練集數據的分布情況,但由於數據本身維度接近100,不能直觀的可視化展示,所以就對降維可視化做了一些粗略的了解以便能在低維空間中近似展示高維數據的分布情況,以下內容不會很深入細節,但足以讓你快速使用這門技術。
什么是降維可視化?
簡而言之,降維是在2維或3維中展現更高維數據(具有多個特征的數據,且彼此具有相關性)的技術。
降維思想主要有兩種:
- 僅保留原始數據集中最相關的變量(特征選擇)。
- 尋找一組較小的新變量,其中每個變量都是輸入變量的組合,包含與輸入變量基本相同的信息(降維)。
什么時候需要用到降維可視化?
如果你的數據集有數十個或者數百個特征,而你想直觀的看出數據集樣本之間的分布情況,那么降到2維或3維來展示這種分布是一個不錯的選擇。
有哪些主流的降維可視化方法?
降維可視化方法其實還挺多的,但是最常見的是以下三種:
- t-SNE
t-分布式隨機鄰域嵌入是一種用於挖掘高維數據的非線性降維算法。 它將多維數據映射到適合於人類觀察的兩個或多個維度。sklearn中已有相應的實現,用起來很方便。 - PCA
主成分分析,是一種線性降維方法,雖然快,但相比非線性降維丟失的信息更多。 - LargeVis
一種在t-SNE之上提出的更快的,效果和t-SNE差不多的降維算法,項目地址:https://github.com/lferry007/LargeVis
t-SNE的原理?
我們知道,數據降維后,數據中的信息是有一定的損失量的,這個損失量在t-SNE方法中,是采用K-L散度來計算的。
K-L散度計算的是“用一個分布q來近似另一個分布p時的信息損失量”,其公式如下:
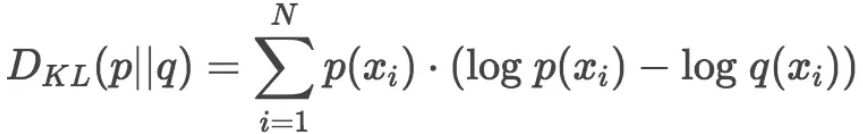
我們知道,對於一組離散型隨機變量{x1,x2,...,xn},其期望值=x1* x1的概率+x2 * x2的概率+xn * xn的概率,所以上式可以用期望值表達成分布p和分布q之間的對數差值的期望,這里對數差值對應之前說的一組隨機變量:
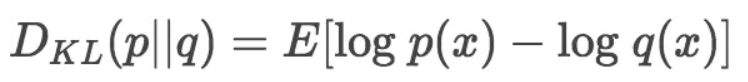
更一般的寫法如下,根據log a - log b = log (a/b):

K-L散度越小,表示信息損失越小,兩個分布越相近。
現在回到t-SNE,我們使用t-SNE是為了將高維數據用低維數據來表達,以便能夠可視化。那么這里就涉及到2種分布,一個是高維數據的分布p,一個是低維數據的分布q,想讓低維數據能夠最好的表達高維的情況,就可以將K-L散度公式做為損失函數,通過最小化散度來學習出q分布下的各樣本點。
目標函數:
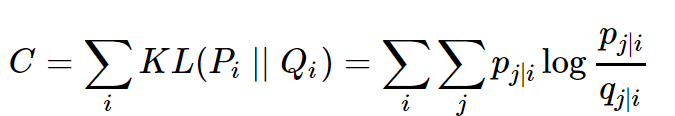
其中:
p分布是基於高斯分布來構建的,表達了兩點之間的相似度,對比高斯公式可以看到,這里用xi表示了總體均值μ,所以這里說的相似度是通過以樣本點i為均值時,樣本點i與其相差幾個標准差來表達的:

q分布也是基於高斯分布來構建的,但是指定了標准差σ=1/√2(即我們規定用這樣的分布來近似高維的分布),所以相比上面少了σ的參數項。

上面說的其實是SNE方法,t-SNE相對SNE的區別如下:
- 使用聯合概率(xi和xj同時出現的概率)代替條件概率(xi出現的條件下xj出現的概率、xj出現的條件下,xi出現的概率),調整后的公式如下:
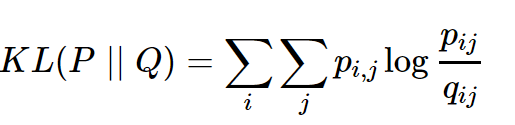
- 低維空間下,使用t分布代替高斯分布表達兩點之間的相似度,調整后的q分布和梯度如下:
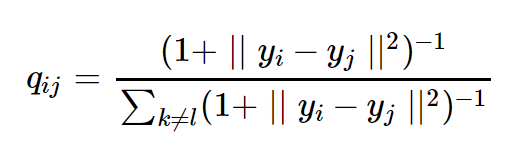
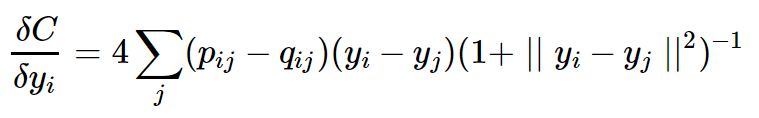
這樣調整后,梯度計算會更加簡潔,並且在這樣得梯度公式下,當遇到高維空間中距離不相近,但是低維空間中距離相近的樣本點,也會產生較大的梯度,讓模型學習到這些點在低維空間中並不靠的近,也就是說這樣會使得高維空間相似的樣本在低維空間靠的更近,高維空間不相似的點在低維空間分的更開,避免SNE經常出現的擁擠(各個簇聚在一起無法區分)問題。
如何使用t-SNE?
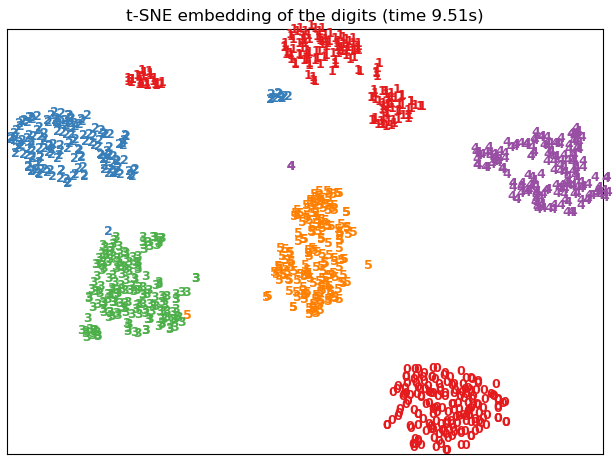
看一個對手寫數字圖片進行二維可視化的例子,效果如下:
代碼如下:
"""
t-SNE對手寫數字進行可視化
"""
from time import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.manifold import TSNE
def get_data():
digits = datasets.load_digits(n_class=6) # 取數字0-5
data = digits.data
label = digits.target
n_samples, n_features = data.shape
return data, label, n_samples, n_features
def plot_embedding(data, label, title):
x_min, x_max = np.min(data, 0), np.max(data, 0)
data = (data - x_min) / (x_max - x_min)
fig = plt.figure()
ax = plt.subplot(111)
for i in range(data.shape[0]):
plt.text(data[i, 0], data[i, 1], str(label[i]),
color=plt.cm.Set1(label[i] / 10.),
fontdict={'weight': 'bold', 'size': 9})
plt.xticks([])
plt.yticks([])
plt.title(title)
return fig
def main():
data, label, n_samples, n_features = get_data()
print('Computing t-SNE embedding')
# 降到2維
tsne = TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
result = tsne.fit_transform(data)
plot_embedding(result, label,
't-SNE embedding of the digits (time %.2fs)'
% (time() - t0))
plt.show()
if __name__ == '__main__':
main()
參考資料:
http://www.datakit.cn/blog/2017/02/05/t_sne_full.html#25-不足
ok,本篇就這么多內容啦~,感謝閱讀O(∩_∩)O。