機器學習-正則化（嶺回歸、lasso）和前向逐步回歸

觀看本文之前，您也許可以先看一下后來寫的一篇補充：https://www.cnblogs.com/jiading/p/12104854.html

本文代碼均來自於《機器學習實戰》

這三種要處理的是同樣的問題，也就是數據的特征數量大於樣本數量的情況。這個時候會出現矩陣不可逆的情況，為什么呢？

矩陣可逆的條件是：1. 方陣 2. 滿秩

X.t*X必然是方陣（nxmxmxn=nxn,最終行列數是原來的X矩陣的列數，也就是特征數),但是要滿秩的話，由於線性代數的一個結論，X.t*X的秩不會比X大，而X的秩是樣本數和特征數中較小的那一個，所以，如果樣本數小於特征數的話，X.t*X就不會是可逆的。

遇到這種情況，我們可以采用正則化的方式或者剔除多余特征，這里我們介紹一些正則化的方式，例如嶺回歸、lasso，以及另外的一種方法：前向逐步回歸

lasso方法效果很好但是計算復雜，前向逐步回歸可以得到和lasso差不多的效果，但是實現起來更加容易

---當然來自於《機器學習實戰》

正則化

先解釋一下這個詞吧，畢竟這個詞，每次聽都感覺很玄妙的樣子，但是也說不清到底哪里玄妙了。

在數學，統計學和計算機科學中，尤其是在機器學習和逆問題中，正則化是添加信息以解決不適定問題或防止過度擬合的過程。 正則化適用於不適定的優化問題中的目標函數。。

來源：https://en.wikipedia.org/wiki/Regularization_(mathematics)

唔，這里知乎有個答主寫的很靠譜，把正則化的概念從頭到尾擼了一遍。這里搬運一下：

先po一下題主題的問題：

機器學習中常常提到的正則化到底是什么意思？

舉個例子 這是個基於多核的支持向量機的目標函數 d是多核函數的參數 它說r(d)是正則項。為什么要令r(d)為正則項，有什么目的？

來源：https://www.zhihu.com/question/20924039，陶輕松的回答

作者：陶輕松

我盡量用通俗一點的話來解答一下樓主的問題，

r(d)可以理解為有d的參數進行約束，或者 D 向量有d個維度。
咱們將樓主的給的凸優化結構細化一點，別搞得那么抽象，不好解釋；

, 其中，
咱們可以令: f() = .

ok，這個先介紹到這里，至於f(x)為什么用多項式的方式去模擬？相信也是很多人的疑問，很簡單，大家看看高等數學當中的泰勒展開式就行了，任何函數都可以用多項式的方式去趨近，log x,lnx,等等都可以去趨近，而不同的函數曲線其實就是這些基礎函數的組合，理所當然也可以用多項式去趨近，好了，這個就先解釋到這里了。

接下來咱們看一下擬合的基礎概念。
首先，用一個例子來理解什么是過擬合，假設我們要根據特征分類{男人X，女人O}。
請看下面三幅圖，x1、x2、x3；

這三幅圖很容易理解：1、 圖x1明顯分類的有點欠缺，有很多的“男人”被分類成了“女人”。2、 圖x2雖然有兩個點分類錯誤，但是能夠理解，畢竟現實世界有噪音干擾，比如有些人男人留長發、化妝、人妖等等。3、 圖x3分類全部是正確的，但是看着這副圖片，明顯覺得過了，連人妖都區分的出來，可想而知，學習的時候需要更多的參數項，甚至將生殖器官的形狀、喉結的大小、有沒有胡須特征等都作為特征取用了，總而言之f(x)多項式的N特別的大，因為需要提供的特征多，或者提供的測試用例中我們使用到的特征非常多(一般而言，機器學習的過程中，很多特征是可以被丟棄掉的)。

好了，總結一下三幅圖：
x1我們稱之為【欠擬合】
x2我們稱之為【分類正擬合】，隨便取的名字，反正就是容錯情況下剛好的意思。
x3我們稱之為【過擬合】，這種情況是我們不希望出現的狀況，為什么呢？很簡單，它的分類只是適合於自己這個測試用例，對需要分類的真實樣本而言，實用性可想而知的低。

恩，知道了過擬合是怎么回事之后，我們來看一下如何去規避這種風險。先不管什么書上說的、老師講的、經驗之說之類的文言文。咱們就站在第一次去接觸這種分類模型的角度去看待這個問題，發散一下思維，我們應該如何去防止過擬合？
顯而易見，我們應該從【過擬合】出現的特征去判別，才能規避吧？
顯而易見，我們應該、而且只能去看【過擬合】的f(x)形式吧？
顯而易見，我們從【過擬合】的圖形可以看出f(x)的涉及到的特征項一定很多吧，即等等很多吧？
顯而易見，N很大的時候，是等數量增長的吧？
顯而易見，w系數都是學習來的吧？

So，現在知道這些信息之后，如何去防止過擬合，我們首先想到的就是控制N的數量吧，即讓N最小化吧，而讓N最小化，其實就是讓W向量中項的個數最小化吧？
其中，W=()

PS: 可能有人會問，為什么是考慮W，而不是考慮X?很簡單，你不知道下一個樣本想x輸入的是什么，所以你怎么知道如何去考慮x呢？相對而言，在下一次輸入,即第k個樣本之前，我們已經根據次測試樣本的輸入，計算(學習)出了W.就是這么個道理，很簡單。

ok,any way.回到上面的思維導圖的位置，我們再來思考，如何求解“讓W向量中項的個數最小化”這個問題，學過數學的人是不是看到這個問題有點感覺？對，沒錯，這就是0范數的概念！什么是范數，我在這里只是給出個0-2范數定義，不做深究，以后有時間在給大家寫點文章去分析范數的有趣玩法；
0范數，向量中非零元素的個數。
1范數，為絕對值之和。
2范數，就是通常意義上的模。

PS，貌似有人又會問，上面不是說求解“讓W向量中項的個數最小化”嗎？怎么與0范數的定義有點不一樣，一句話，向量中0元素，對應的x樣本中的項我們是不需要考慮的，可以砍掉。因為沒有啥意義，說明項沒有任何權重。so，一個意思啦。

ok，現在來回答樓主的問題，r(d) = “讓W向量中項的個數最小化” =

**所以為了防止過擬合，咱們除了需要前面的相加項最小，即樓主公式當中的
= 最小，我們還需要讓r(d)=最小，所以，為了同時滿足兩項都最小化，咱們可以求解讓和r(d)之和最小，這樣不就同時滿足兩者了嗎？如果r(d) 過大，再小也沒用；相反r(d)再小，太大也失去了問題的意義。
說到這里我覺得樓主的問題我已經回答了，那就是為什么需要有個r(d)項，為什么r(d)能夠防止過擬合原因了。

**
根據《男人幫》電影大結局的劇情：本來故事已經完成了，為了讓大家不至於厭惡課本的正規理論，我們在加上一集內容，用以表達我對機器學習出書者的尊重；

書本中，或者很多機器學習的資料中，為了讓全球的機器學習人員有個通用的術語，同時讓大家便於死記硬本，給我上一段黑體字的部分的內容加上了一坨定義，例如：
我們管叫做經驗風險，管上面我們思維導圖的過程叫做正則化，所以順其自然的管r(d)叫做正則化項，然后管+r(d) 叫做結構風險，所以順其自然的正則化就是我們將結構風險最小化的過程，它們是等價的。
By the way，各位計算機界的叔叔、阿姨、伯伯、嬸嬸，經過不懈的努力，發現了這個公式很多有意思的地方，它們發現0范數比較惡心，很難求，求解的難度是個NP完全問題。然后很多腦袋瓜子聰明的叔叔、阿姨、伯伯、嬸嬸就想啊，0范數難求，咱們就求1范數唄，然后就研究出了下面的等式：

一定的條件我就不解釋了，這里有一堆算法，例如主成分KPCA等等，例子我就不在舉了，還是原話，以后我會盡量多寫點這些算法生動點的推到過程，很簡單，注重過程，不要死記硬背書本上的結果就好。上面概括而言就是一句話總結：1范數和0范數可以實現稀疏，1因具有比L0更好的優化求解特性而被廣泛應用。然后L2范數，是下面這么理解的，我就直接查別人給的解釋好了，反正簡單，就不自己動腦子解釋了： L2范數是指向量各元素的平方和然后求平方根。我們讓L2范數的正則項||W||2最小，可以使得W的每個元素都很小，都接近於0，但與L1范數不同，它不會讓它等於0，而是接近於0，這里是有很大的區別的哦；所以大家比起1范數，更鍾愛2范數。所以我們就看到書籍中，一來就是，r(d)= 這種結構了，然后在機器學習當中還能看到下面的結構：min{ } ，>=0都是這么來的啦，萬變不離其中。

講一點自己機器學習過程的體驗，大家都覺得機器學習入門難，絕大部分人反應知其然不知其所以然，這個原因很多時候在於中國教育工作者的教學、科研氛圍，尤其是中文書籍出書者自己都不去搞懂原理，一個勁的為了利益而出書、翻譯書，純粹利益驅動。再加之機器學習起源於國外，很多經典的、有趣的歷史沒有被人翻譯、或者歸類整理，直接被舍棄掉了。個人感覺這是中國教育的缺失導致的。希望更多的人真的愛好計算機，愛好機器學習以及算法這些知識。喜歡就是喜歡。希望國內機器學習的愛好者慢慢的齊心合力去多多引薦這些高級計算機知識的基礎。教育也不是由於利益而跟風，AI熱出版社就翻譯AI，機器學習熱就翻譯機器學習，知識層面不斷架空，必然導致大家學習熱情的不斷衰減！願共勉之。

所以從定義上來看，原本用來進行正則化的是0范數，但是由於計算困難，大家才轉而使用2范數的。

嶺回歸

先貼一張《機器學習實戰》的圖哈

加入偏差：犧牲無偏性

加一點百度百科的數學性解釋（感覺又回到了那個被數值分析支配的學期。。。）

來源：https://baike.baidu.com/item/%E5%B2%AD%E5%9B%9E%E5%BD%92

對於有些矩陣，矩陣中某個元素的一個很小的變動，會引起最后計算結果誤差很大，這種矩陣稱為“病態矩陣”。有些時候不正確的計算方法也會使一個正常的矩陣在運算中表現出病態。

當X不是列滿秩時，或者某些列之間的線性相關性比較大時，的行列式接近於0，即 時誤差會很大，傳統的最小二乘法缺乏穩定性與可靠性。

為了解決上述問題，我們需要將不適定問題轉化為適定問題：我們為上述損失函數加上一個正則化項，變為

其中，我們定義，於是：

上式中，是單位矩陣。

隨着的增大，的絕對值均趨於不斷變小，它們相對於正確值 趨於無窮大時， 趨於0。其中，隨的改變而變化的軌跡，就稱為嶺跡。實際計算中可選非常多的 值，做出一個嶺跡圖，看看這個圖在取哪個值的時候變穩定了，那就確定 值了。

嶺回歸是對最小二乘回歸的一種補充，它損失了無偏性（就是計算沒有偏差的意思），來換取高的數值穩定性，從而得到較高的計算精度。

知乎上有位答主說的很透，這里轉一下:

來源：https://www.zhihu.com/question/28221429，某知乎用戶的回答

所以具體實施其實挺簡單的。但是注意，“為了使用嶺回歸和縮減技術，首先要對特征做標准化處理，使得每個維度的特征具有相同的重要性”,注意這里的“標准化”指的其實是Standardization，是改變了原有分布、變成均值為0方差為1的。具體可以看這篇博文：https://www.cnblogs.com/jiading/p/11575038.html

為什么要標准化，因為很明顯，由文章最上面的議論我們可以看出來，在損失函數中加入二范數懲罰項是為了能將一些不必要的w設置為0，這才是嶺回歸的真正目的，而不僅僅是為X.t/*X“撐場子”保證其可逆。所以，我們可以想象，如果不標准化的話，一些y_i會變的非常大，那么通過公式，我們就很難將這些項對應的w設置為0，而它們卻是有可能是不相關的。所以，我們必須讓每一項都有一樣的“重要性”。使用Standardization之后，連每個特征的樣本分布都給你整一樣的了，這才是真正的“泯然眾人矣”。

特征的值的大小不重要，我們看的關鍵是它是否和我們要回歸的量相關

嶺回歸的代碼其實比較簡單：

#嶺回歸
def ridgeRegres(xMat,yMat,lam=0.2):
    xTx = xMat.T*xMat
    denom = xTx + eye(shape(xMat)[1])*lam
    if linalg.det(denom) == 0.0:
        print ("This matrix is singular, cannot do inverse")
        return
    ws = denom.I * (xMat.T*yMat)
    return ws
#嶺回歸的測試函數    
def ridgeTest(xArr,yArr):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    #數據必須先標准化，才能進行正則化
    yMat = yMat - yMean     #to eliminate X0 take mean off of Y
    #regularize X's
    xMeans = mean(xMat,0)   #calc mean then subtract it off
    xVar = var(xMat,0)      #calc variance of Xi then divide by it
    xMat = (xMat - xMeans)/xVar
    numTestPts = 30 
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        #讓λ以指數級變換，只是為了看λ很小和很大的時候對結果的影響 
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat 

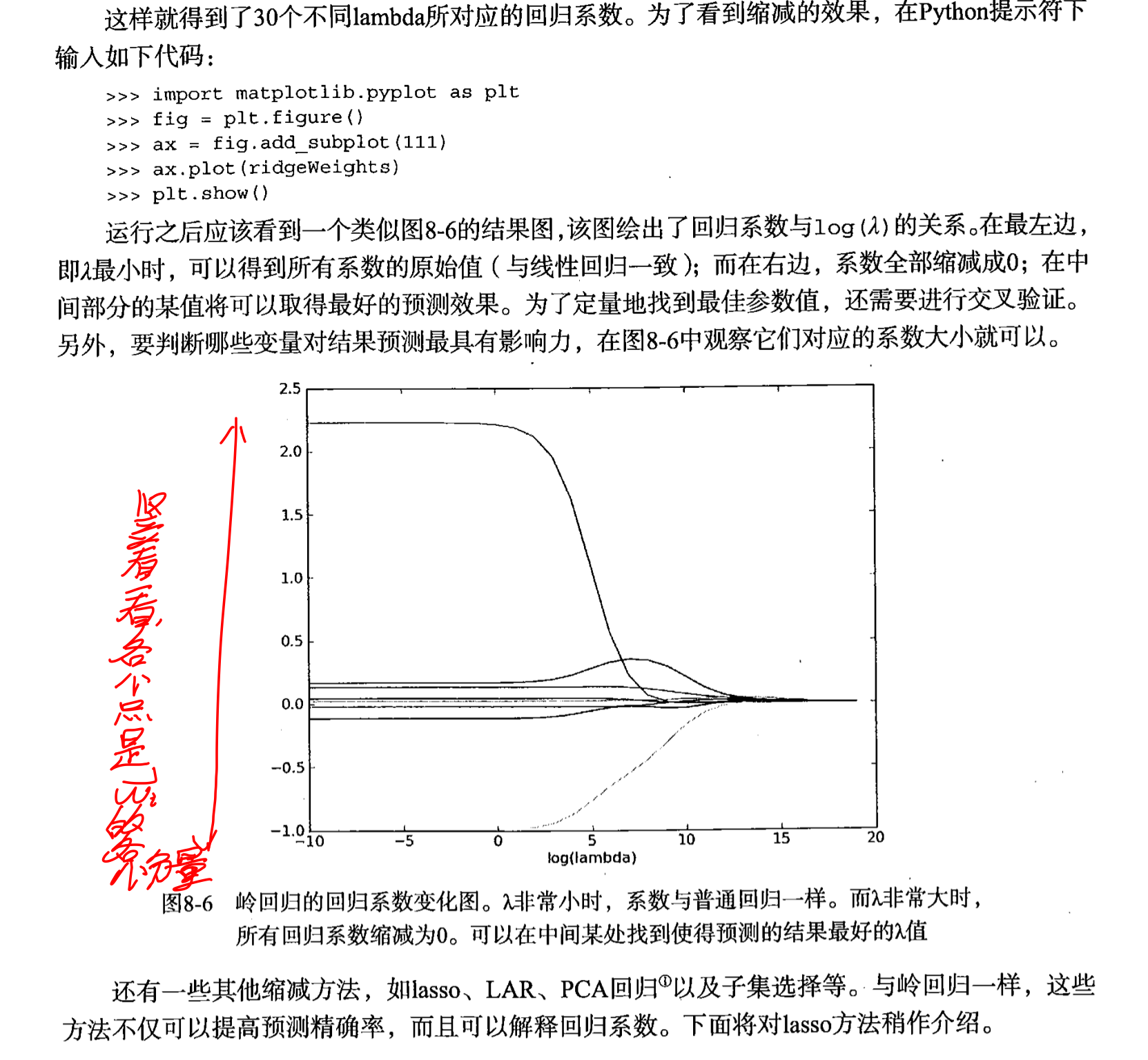
這張圖非常好！它直觀地體現了上面說的正則化對w的懲罰作用：當λ設置較大的時候，幾乎所有的參數都被懲罰到了接近0的地步，注意是接近0但不是0！

為什么不是0，這一點留到下面講lasso的時候對比着說比較清楚

lasso

lasso和嶺回歸的唯一區別就是將使用的二范數換成了一范數。但是再引出lasso的公式之前，我們需要先把嶺回歸的公式修改一下：

這里借用了知乎少整醬的回答中的公式（https://zhuanlan.zhihu.com/p/30535220）

cost function的形式就為:

通過加入此懲罰項進行優化后，限制了回歸系數wiwi的絕對值，數學上可以證明上式的等價形式如下:

其中t為某個閾值。

同學們，這里用到的是什么啊？用到的就是拉格朗日乘子法和KKT條件啊，下面的就是不等式約束，把t往左邊一挪，就是熟悉的不等式約束的形式了。只不過那個t我們沒有在代價函數里面體現，但是這也沒什么影響，因為代價函數一求偏導數這些常數就都沒有了。

那么類似的，lasso方法只是將上面的公式修改為了：

也就是用了一范數，但就是這一個范數的差別就造成了很大的不同：

L2范數是指向量各元素的平方和然后求平方根。我們讓L2范數的正則項||W||2最小，可以使得W的每個元素都很小，都接近於0，但與L1范數不同，它不會讓它等於0，而是接近於0

而對於lasso方法，則是會讓一些系數真的為0.這一點從幾何上比較好解釋，這里再借用一下知乎少整醬的回答：

嶺回歸的幾何意義

以兩個變量為例, 殘差平方和可以表示為 的一個二次函數，是一個在三維空間中的拋物面，可以用等值線來表示。而限制條件 ， 相當於在二維平面的一個圓。這個時候等值線與圓相切的點便是在約束條件下的最優點，如下圖所示，

LASSO的幾何解釋

同樣以兩個變量為例，標准線性回歸的cost function還是可以用二維平面的等值線表示，而約束條件則與嶺回歸的圓不同，LASSO的約束條件可以用方形表示，如下圖:

相比圓，方形的頂點更容易與拋物面相交，頂點就意味着對應的很多系數為0，而嶺回歸中的圓上的任意一點都很容易與拋物面相交很難得到正好等於0的系數。這也就意味着，lasso起到了很好的篩選變量的作用。.

是不是說的特別清楚！

雖然懲罰函數只是做了細微的變化，但是相比嶺回歸可以直接通過矩陣運算得到回歸系數相比，LASSO的計算變得相對復雜。由於懲罰項中含有絕對值，此函數的導數是連續不光滑的，所以無法進行求導並使用梯度下降優化。本部分使用坐標下降發對LASSO回歸系數進行計算。

看到這里，同學可能有疑問了：那不能用梯度下降法，為什么不用正規方程法呢？因為正規方程法也是基於求導的呀，忘了的同學看下圖（來源：https://blog.csdn.net/qq_36523839/article/details/82931559）

所以只能用坐標下降法。

https://zhuanlan.zhihu.com/p/30535220上有具體的坐標下降法的方法和python實現，我就不轉了，主要是我也懶得學了2333，（據說）比它更方便的前向逐步回歸可以得到和它類似的效果，那這個就不看了。

前向逐步回歸

這個算法聽着挺玄乎，其實看代碼就知道，是屬於比較無腦和暴力的方法，效率不會太高。當然實現起來是真的簡單。

代碼：

'''
Created on Jan 8, 2011

@author: Peter
'''
from numpy import *
#加載數據
def loadDataSet(fileName):      #general function to parse tab -delimited floats
    #attribute的個數
    numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields 
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        #dataMat是一個二維矩陣，labelMat是一維的
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat
def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
    return ((yArr-yHatArr)**2).sum()
def regularize(xMat):#regularize by columns
    inMat = xMat.copy()
    inMeans = mean(inMat,0)   #calc mean then subtract it off
    inVar = var(inMat,0)      #calc variance of Xi then divide by it
    inMat = (inMat - inMeans)/inVar
    return inMat
#前向逐步線性回歸，目的是輸出線性回歸的weight
def stageWise(xArr,yArr,eps=0.01,numIt=100):
    #eps是每次迭代的步長，numIt是迭代的次數
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    #標准化,x的標准化使用的是Z-score Normalization，其實是Standardization，改變了原有分布的
    yMat = yMat - yMean     #can also regularize ys but will get smaller coef
    xMat = regularize(xMat)
    #m是樣本個數，n是特征數
    m,n=shape(xMat)
    #保存每次迭代之后的結果，測試時候顯示迭代過程用的，真正使用的時候只要最后一次就好了
    returnMat = zeros((numIt,n)) #testing code remove
    #初始的時候所有的weights置為0
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
    for i in range(numIt):
        print (ws.T)#輸出現在的weight
        lowestError = inf; 
        #對每個變量的系數進行嘗試
        for j in range(n):
            #注意這里不是在-1到1的范圍內遍歷，而是遍歷數組，這個數組中有-1和1兩個元素
            for sign in [-1,1]:
                wsTest = ws.copy()
                #改變一個變量的值，或者加上一個步長，或者減去一個步長
                wsTest[j] += eps*sign
                yTest = xMat*wsTest
                #計算誤差
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    #如果誤差比最小誤差小，這個weight的“配方”就留下了
                    lowestError = rssE
                    wsMax = wsTest
        #最后留下那個最大的weight的配方
        ws = wsMax.copy()
        returnMat[i,:]=ws.T
    return returnMat