吉哈地址:
>>>https://github.com/DreamFeather/031702113<<<
更新記錄
2019/9/30:程序運行時發現不可重現Bug,有幾率導致程序停止運行。錯誤源自Koe::~Koe()中刪除block指針時,錯判用已經刪除的number。已更正。

2019/9/30:博客內容刪改:調整字體大小;PSP表格修改;添加流程圖;添加拓展思考;重新進行代碼分析;完善實例測試;
### PSP表格:
| PSP2.1 | Personal Software Process Stages | 預估耗時(分鍾) | 實際耗時(分鍾) |
|---|---|---|---|
| Planning | 計划 | 15 | 15 |
| Estimate | 估計這個任務需要多少時間 | 15 | 15 |
| Development | 開發 | 320 | 660 |
| Analysis | 需求分析 (包括學習新技術) | 20 | 120 |
| Design Spec | 生成設計文檔 | 0 | 0 |
| Design Review | 設計復審 | 30 | 0 |
| Coding Standard | 代碼規范 (為目前的開發制定合適的規范) | 0 | 0 |
| Design | 具體設計 | 20 | 120 |
| Coding | 具體編碼 | 120 | 150 |
| Code Review | 代碼復審 | 10 | 30 |
| Test | 測試(自我測試,修改代碼,提交修改) | 120 | 240 |
| **Reporting ** | 報告 | 160 | 320 |
| Test Report | 測試報告 | 20 | 120 |
| Size Measurement | 計算工作量 | 20 | 20 |
| Postmortem & Process Improvement Plan | 事后總結, 並提出過程改進計划 | 120 | 180 |
| 合計 | 495 | 995 |
解題思路
看到題目是數獨的時候,我大腦里第一反應是,游戲,數學家沒事時玩的,一張報紙大的紙,一支鉛筆,擦擦寫寫。好吧,這個游戲我聽說過,但是從來沒玩過,所以做的第一件事,在手機上裝個數獨游戲玩玩。這里我推薦“數獨專業版”app,沒有廣告,界面簡潔,小米商店評分4.9,下載來體驗一把做數學家的驚險與刺激,簡直是不二選擇。邊玩邊思考,玩了兩盤,靈感就來了。
首先,解一個數獨題,其實就三步走:
第一,是最基本的,要知道哪些格子里有數,哪些格子沒數。
第二,是最關鍵的,沒數的格子里可以填哪些數。
第三,是最重要的,如何把格子填滿。
第一步,用一個很簡單的if語句就可以判斷出哪些格子有沒有數,沒有數的要記錄下來。我把它們放到一個隊列里,排隊等候填數
for (int i = 0; i != max; ++i)
{
number[i] = new int[max];
for (int j = 0; j != max; ++j)
{
number[i][j] = array[i][j]; //這里其實是Koe(宮格)類的初始化過程
if (number[i][j] == 0)space_x.push(i), space_y.push(j); //順便找一下待處理的格子,將其坐標存入隊列space
else if (divided)block[int(i*div_x)][int(j*div_y)][number[i][j]] = 1;//划分塊,沒宮的用不着
}
}
第二步,如果一個格子沒數,如何得到它能填的數呢?從游戲規則上來講是橫豎不重復,分塊內不重復。那就得從已存在的數入手
void Koe::available(int i, int j, queue<int> &rest) //找尋i行j列元素可用數,存放在rest隊列
{
int m = 0, max_ = max + 1;
int *exist = new int[max_]; //因為要以存在數的值作為下標,所以得多開一點空間
while (m != max_)exist[m++] = 0;
for (m = 0; m != max; ++m)
{
exist[number[i][m]] = 1; //橫豎同時判斷,一個循環搞定
exist[number[m][j]] = 1; //不用跳過自己,反正必定有number[i][j]=0,再加判斷只是空耗開銷
}
if (divided) //從分塊里再看
{
int x = int(i *div_x), y = int(j *div_y); //用i,j乘以分塊划分比,即可得出i,j所在分塊下標
for (int z = 1; z != max_; ++z)
{
if (block[x][y][z] == 1)exist[z] = 1; //block[x][y][z]=1的意思是,分塊[x][y]中存在數字z
}
}
m = 1; //從1開始記錄
while (m != max_)
{
if (exist[m] == 0)rest.push(m); //不存在的放入可用隊列rest
++m;
}
delete []exist; //new出來的數組可以刪了
exist=NULL;
}
第三步,怎么把格子填滿?我用的是遞歸的方法,逐個處理在Koe初始化的時候,我已經把空位存入了隊列space,所以我只要一個一個取出來填就行了,填什么?上面的的available方法已經給了答案(以下源碼經過簡化)
int Koe::deduce(queue<int>s_x,queue<int>s_y)
{
int x = s_x.front(), y = s_y.front();
queue<int> rest;
available(x, y, rest); //就當前位置找可用數字
s_x.pop(), s_y.pop();
int blk_x = int(x *div_x), blk_y = int(y * div_y);
int record = number[x][y]; //記錄當前數字,保存現場。很沒必要,我知道它一定是0
int answer = 0;
while (!rest.empty()) //可用數字不為空,就一直找下去
{
number[x][y] = rest.front(); //填一個數字
rest.pop();
if (divided)block[blk_x][blk_y][number[x][y]] = 1; //填好數字后相應的分塊里要置1,表示占用
if (!s_x.empty())answer += deduce(s_x, s_y); //進入下一階填空
......
if (divided)block[blk_x][blk_y][number[x][y]] = 0; //分塊內數字取消占用
}
if (s_x.empty()) //空填完了,即找到了答案
{
......
}
number[x][y] = record; //恢復數字,等於0即可
return answer;
}
整個項目,主角就是Koe一個類,里面裝的有點多,結構如下  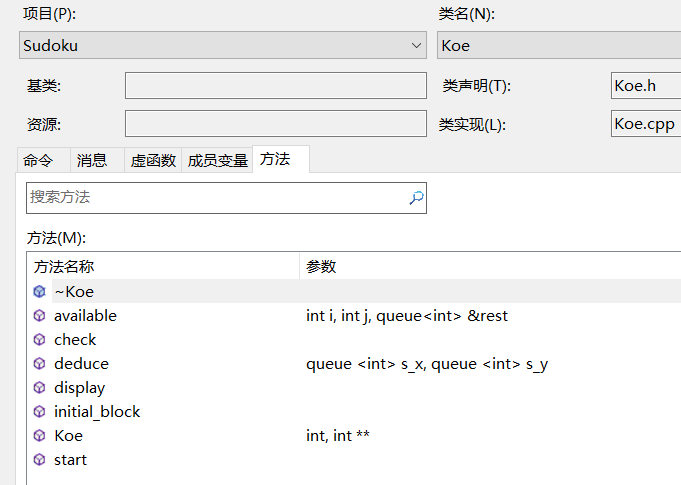
Sudoku里的main處理流程 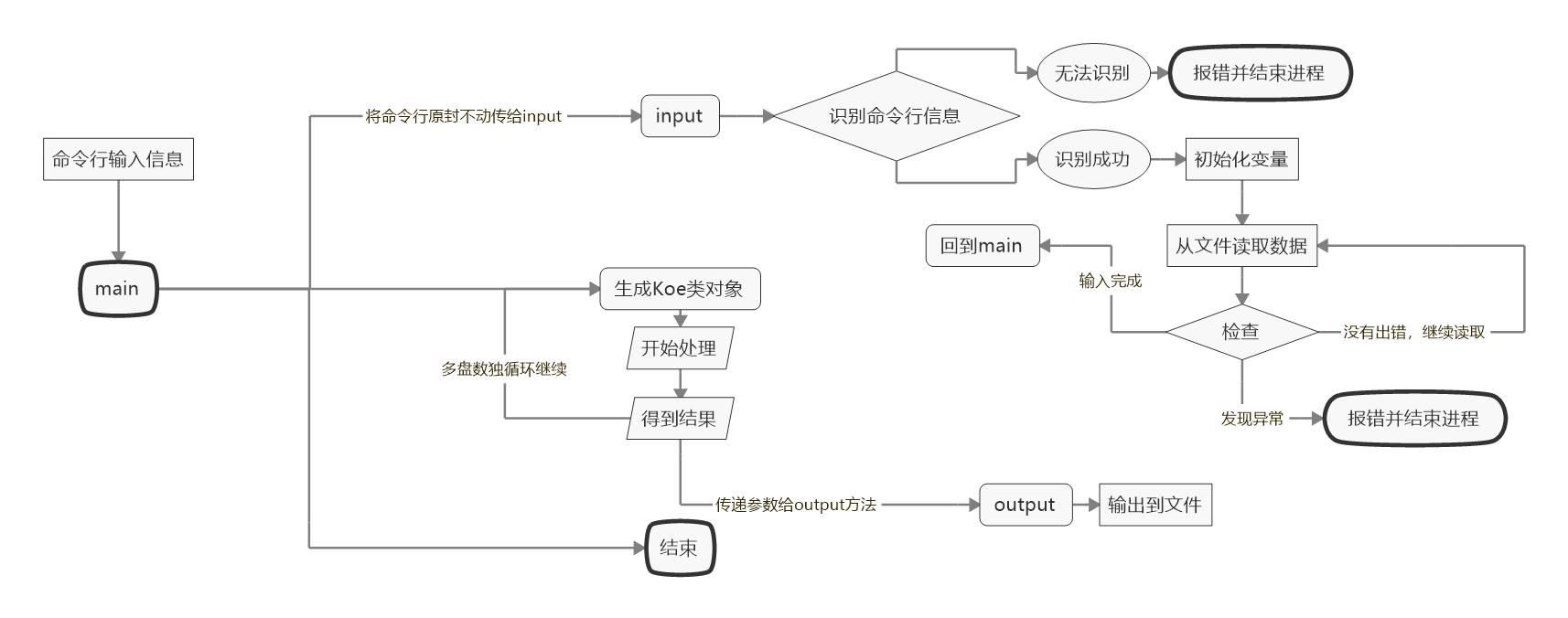
Koe類里的處理流程(略微簡化) 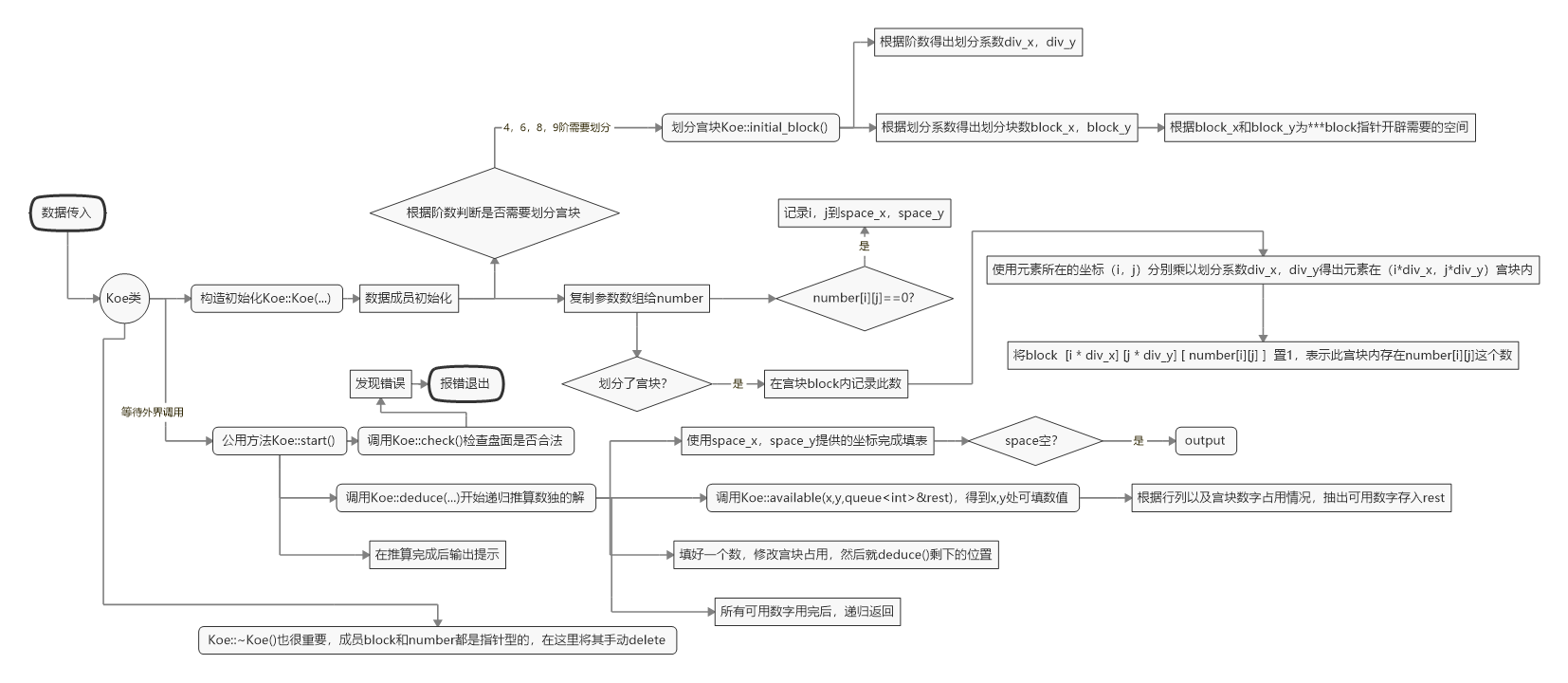
很多人會這覺得,解出數獨即是完成了這次作業。解數獨確實是這個項目的主要需求,也是整個項目構建起手之處,當然不排除有些人先構建IO啦。我是從解數獨Koe類開始的,但是從新建一個項目到屏幕上可以正確輸出只過了40分鍾,准確地說43分鍾,比我預想的要快得多。我想了想,我做完了嗎?沒有。停下來思考一下,總體完成度大概在66%左右,IO我還沒處理呢。
這次作業還有一個關鍵點在於——對命令行的輸入處理
並且,在作業要求里也有明確提到,對於錯誤的處理。我想了想,對於錯誤處理,在內部數據結構正確的情況下,出錯基本是因為對輸入處理得不夠嚴謹,用正確的算法處理錯誤的數據,當然不會得到正確得結果。
我的目標是:對於任何輸入,我的程序都能夠有相應的反應。
- 只要命令參數里敘述的信息邏輯正確,符合規定,我就一定能提取出正確有效的信息。比如規定-m后是數獨階數,那么-m 3,3在-m后面,我就知道了,3帶代表求解的數獨階數。
- 只要從命令行里能得到足夠的、有效的輸入信息,我的程序就一定能輸出正確結果。
- 得不到足夠的、有效的信息,或者無法識別輸入信息,一定要有相應的錯誤提示,告訴用戶有錯誤,可能錯在哪里。
錯誤處理考慮:
-
命令行參數個數,最基本是要考慮到是有9個參數,Sudoku.exe -m 宮格階數 -n 數獨盤數 -i 輸入文件 -o 輸出文件,不是你期望的個數肯定就錯了。我的為了實現多點的功能,參數有9,10,11三種可能。
-
命令行參數順序,作業要求的原話是:“從-m之后獲取盤面階數,-n之后獲取盤面數量,-i之后獲取輸入文件名,-o之后獲取輸出文件名。”輸入順序我不知道,我只知道從某個命令后獲取到的數據代表什么,只要信息邏輯表達正確,我就能獲取到正確有效的信息。
-
參數讀到程序里來了,雖然正確有效符合邏輯,但還得確認它在我程序能處理的范圍內。宮格階數,整數范圍[3,9];數獨盤數,整數大於0就好;輸入文件,首先能打開就好;輸出文件的話,要求不高,不要和我的命令(-m,-n,-i,-o等)重名,(輸出文件路徑的問題有待考慮)。
-
命令行的參數考慮到這里。另一個輸入是在文件里,首先,我已經找到了,但是里面的數據不對,我肯定也處理不了。所以,先判斷,文件有沒有足夠的內容,在讀的過程中,要檢查是否讀到文檔末尾了,我沒讀完就沒了,那肯定不對,要報錯,不是階數錯了就是文件錯了。
-
文件內容人眼看上去是夠的,5X5矩陣,9X9矩陣,非常整齊。但是萬一其中插入了非數字字符呢?我測試過,fstream對象輸入字符數據到int類型,程序可以是直接掛的,當場閃退。用戶一臉黑人問號:閃一下就沒了???辣雞軟件!!!用戶肯定不會想到是自己的輸入文件有問題,尤其還是那種喜歡把測試用例文件改來改去的(比如我室友 (눈_눈!) ),打上了一個字符也毫不知情,后面測試兩小時你其實能想到我們在干嘛了,簡直害skr人。好吧,在文件里檢測到字符了或者其他非數字的輸入,報錯,精准到幾行幾列,檢查盤數的時候輸出現在是檢查第幾盤,所以報錯后我們能迅速找到錯誤。
-
對於輸入的處理我還不敢保證絕對完美,畢竟我個人的精力和腦回路是有限的,我暫時已經想不出還會有其他我沒考慮到情況了。實際上我可能已經過度考慮了:雖然atoi函數只能返回int型,但要是階數盤數輸入出現小數我也會輸出警告。此時,雖然程序已經獲得到了可用有效的信息,但是我還是遺憾地選擇終止進程,因為輸入不符合規范,規范是整數。比如-m 3.8,我用atoi轉換一下只能得到3,但是在*argv[]里我仍然能找到一個'.',基於人性化考慮我可以讓它以3接着運行下去;基於嚴謹性我認為我獲得了一個有效信息3,可是這個有效信息3和用戶輸入的原始信息3.8所表達的信息有出入。我該如何在這兩者之間選擇或者權衡?我最終還是選擇了嚴謹。
錯誤處理相關輸出

再到頭來看,可能會有人覺得可笑了,因為用戶輸入小數的可能性很小啊,用戶自己是想輸入整數的,他也清楚自己要是輸入小數那絕對也不對,總之輸入的可能性超級小,而且還有atoi替我處理......好吧,不討論這個了,越討論越覺得這個處理沒必要。
拓展思考
數獨的無解,可以分為兩種:一階無解和高階(潛在)無解(我說的)。
一階無解:是指初始數字分布很不巧,使得有些空格無數可填。就像這個:

一眼看過去就能看出(1,1)無數可填。一個空位被其他位置制約我把它叫做一階無解。
高階(潛在)無解:是指初始時,每個空位都有可用的數字,但實際上這些空位的可用數字又有一些制約關系(即游戲規則),就是:你用了3,我就不能用3,我還有5可以用,那他也就不能用5了,要用其他的數字。而有的時候這些制約恰好使得這些空位可用數字不夠用,而出現無解,就像6個空位,單獨看,每個空位都可以填一個或者幾個數,但又因為他們之間的制約關系,加起來不重復的可用數字卻只有5個,6個空,5個數不重復當然填不了。但是通常情況下,我們都會去找這些數字的排列組合,以為換一個方式就有解了,其實不然,本身就無解。

讓我們再用一下這個詞 “一眼看過去”,覺得沒什么大問題。如果再一算,發現,確實出現了三個空只能用兩個數的情況。無解吧,但是一般的遞歸非常的不甘心,都找到最后一個空了,前面填過的空換個數再試試,也只是徒勞而空耗性能資源。仔細一看,你就會發現,最后那個宮塊,填不了3,被行列占用了。細看宮格規則發現,規則里規定,每個數字在每個宮格內必須出現並僅出現一次,所以這個是因為宮格的存在而多出來的一條規則、一個制約關系。
猜想:
制約規則多,制約關系太強,所以導致高階無解出現。那么制約關系弱一點的3、5、7階宮格又會怎樣呢?我很快就大膽地斷言:3、5、7階宮格,因為制約關系較弱,所以要無解只會出現一階無解,不會出現高階無解的情況。我馬上又回想到我的算法又可以優化了,3、5、7階只需判斷一階無解就可知道有無解,判定一階有解后,在推算解的過程中我就可以避開繁瑣的有無解處理。腦細胞過度活躍的我發出了曾小賢的經典笑聲,當時甚至還覺得3階太簡單可直接跳到5階,並試圖證明,沒有宮格,就不會出現高階無解。我馬上開始繪圖,以填圖的形式來證明並理清證明思路。哪有啊,就是瞎想幾個例子,嘗試找到制約因素過多會直接出現一階無解而中間不會高階無解的例子。繪圖過程中我逐漸恢復了理智,定了一個模型:陸續添加數字,讓5階數獨(1,1)處出現在不出現一階無解的情況下出現高階無解。
第一步,在第一列加上2,3,4。使得(1,1)處只能用1和5(如果第一列填4個數的話,容易出現一階無解)

第二步,在第二列填上3,2,4,1。使得(1,2)處必定占用第一行的5

第三步,在第三列填上5,4,3,2。使得(1,3)處必定占用第一行的1

第四步,哎?(1,1)處好像已經出現了高階無解???那我已經證明成功了,我成功證明了5階數獨可以有高階無解。興奮透頂的我又發出了曾小賢的經典笑聲。
等我冷靜下來才發現!我要證明的是:3、5、7階數獨不存在高階無解......(笑容逐漸消失)
同樣的我馬上又發現了3階的高階無解,哦豁,7階我想就不用證了吧。
這就是不動腦筋空動手的后果,白高興一場。
好吧,其實我也並不是一無所獲,至少我證明了3、5、7階是存在高階無解的,嘻嘻嘻。

可改進的地方
在寫博客的過程中,我能想到很多在之前沒有想到的事。
- 我覺得寫代碼的同時加上注釋是一個十分重要的規范。在這里我把它當作規范而不是說好習慣,因為習慣看個人,規范看集體。我之前就把寫注釋當作習慣來看待,好壞與否我不是特別在乎。但是現在,我必須得注意了,除了有時候我自己看糊塗外,也是為了別人能更快地理解並讀懂。寫博客,大大地增加了我們代碼的曝光度,寫好注釋,很重要。
- 代碼結構還有需要改進的地方,首先是數獨找0處理,還有優化的地方。我現在的處理方式是,從(0,0)掃瞄到(m,m)處,那么找出來的0的坐標在space隊列里也是沿從坐到右,從上到下排列下來的,之后我直接就用這個順序來執行遞歸搜索了,這種算法缺點就是沒有優先度,若是碰到像上面那個6階高階無解,那一定會把所有排列組合找完才罷休。除了高階無解,也許還會出現...額再造一個概念——假性高階無解?,實際上是有解的,只要返回去改幾個數就可以了。我想到的更優的算法是,將space隊列里的坐標以該處可用數字個數從少到多進行一次排序,也就是可用數字更少的優先填,不然其他的地方先占用了,遞歸就要逐級返回搜索,直到將占用的地方改掉,才能繼續往下走。如果真的無解,那么也能很快就發現,可用數字少的地方都填不下去了,就是無解的標志。再者畢竟題目要求只要一個解,最好的情況就是一路填下去填到最后一個space,把可用數字少的地方先填了,大概率實現所謂的一次找到,就算沒有找到,遞歸返回的次數也會更少,這樣遞歸深搜性能能得到極大優化。
- 我還是有點糾結那個命令行輸入的操作,小數就不討論了,我覺得能優化的地方是對於輸出文件怎么決定,因為對於目前來說我在-o后面隨便打什么(除了命令),它都能接受,比如-w,甚至亂碼,dgh1214,它打不開它也能新建一個,而且文件用txt格式打開后也一字不差,這樣太隨意了。我目前能想到的就是判斷輸出文件路徑最后四個字符是不是.txt,不是就不行。或者我可以人性化一點給它加上后綴?但是軟工老師在課上說過這么一句話:“不是用戶提出來的要求不要去做,做了白費精力。”所以嘞,考慮到嚴謹性我還是稍微做一下規范,僅輸出一句提醒,不終止進程,僅此而已。
代碼分析
以下,多圖警告!(→ܫ→)
這是用m6n5的例子的性能分析。

cpu占用最高達到40%,當然不夠准確,應該是VS性能工具啟動造成的。這種控制台窗口程序一般只會跑一個核,而我的電腦是四核,理論占用不超過25%,以我以往的經歷,其實實際最高可以達到34%(死循環跑法)。並且我有留意,長時間耗cpu的程序,依系統調度會將其占用平均值控制在25%左右。比如這張圖,5階數獨求10000解用了10分鍾多(性能檢測嚴重影響程序運行速度,實際只需40s),其占用就穩定在25%以下,單核並未跑滿。(8分20秒之后我在使用電腦,導致占用偏高)

下面這張圖展現的是sudoku.exe的調用樹,一眼看過去,一個叫_stdio_common_vfprintf的函數獨占時間最高,是關於輸出的函數。我的窗口程序是有一些文字輸出的,不過這個占用比例比我想象的要高得多,性能瓶頸在這,需要減少控制台輸出來獲得更快的運行速度。不過對比於之前,我已經優化過了,刪掉了不必要的輸出。


我依然好奇的是,我覺得最耗時的函數竟然沒有上榜。
Koe::check()是用來檢查數獨盤面是否符合規范的,兩層循環O(m^2),內層宮格空處調用Koe::available()尋找可用數字,復雜度O(2m);檢測行列沖突,O(m);划分宮塊內沖突兩層循環,O((m * div_x * m * div_y)。所以Koe::check()總復雜度為O(m^2 * (m+2m+(m^2)))=O(g(m) * m4+3m3)(令g(m)為階數m的划分系數div積,取值1/9,1/8,1/6,1/4,1),6階就是1/6 * 6^4+3 * 6^3=4 * 6^3,不低了。
Koe::deduce()遞歸推算,令有k個0,每次都調用Koe::available(),復雜度O(k*m)不高於O(m^2),理想情況下確實不高。
Error是不能有的,Warning也不行。以至於double強轉int我都顯示轉換了

實例測試
基本測試:
九階

八階


七階

六階


五階

四階

三階

拓展測試:
命令提示

文檔輸入檢測

多解模式(求40個)

小小的錯誤提示

全解模式的話,可能要等一會了

16W+個,真實!

