一篇文章就搞懂啦,這個必須收藏!
我們以圖片分類來舉例,當然換成文本、語音等也是一樣的。
-
Positive
正樣本。比如你要識別一組圖片是不是貓,那么你預測某張圖片是貓,這張圖片就被預測成了正樣本。 -
Negative
負樣本。比如你要識別一組圖片是不是貓,那么你預測某張圖片不是貓,這張圖片就被預測成了負樣本。 -
TP
一組預測為正樣本的圖片中,真的是正樣本的圖片數。 -
TN:
一組預測為負樣本的圖片中,真的是負樣本的圖片數。 -
FP:
一組預測為正樣本的圖片中,其實是負樣本的圖片數。又稱“誤檢” -
FN:
一組預測為負樣本的圖片中,其實是正樣本的圖片數。又稱“漏檢”。 -
精度(accuracy)
分類正確的樣本數占總樣本數的比例。
acc = (TP+TN)/ 總樣本數 -
查准率/准確率 precision
一組預測為正樣本的圖片中,真的是正樣本的圖片所占的比例。
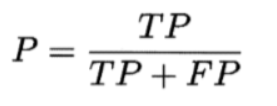
為什么有了Accuracy還要提出Precision的概念呢?因為前者在測試樣本集的正負樣本數不均衡的時候,比如正樣本數為1,負樣本數為99時,模型只要每次都將給定的樣本預測成負樣本,那么Accuracy = (0+99)/100 = 0.99,精度依然可以很高,但這毫無意義。但是同樣的樣本集,同樣的方法運用到查准率公式上,就不可能得到一個很高的值了。
-
查全率/召回率 recall
所有真的是正樣本的圖片中,被成功預測出來的圖片所占的比例。
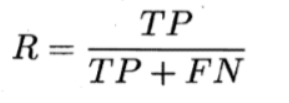
-
查准率和查全率的關系
一般來說,想查的准,那么往往查不全(想想寧缺毋濫);想查的全,又往往會不准(想想寧抓錯不放過)。所以P和R是兩個矛盾的量。 -
P-R曲線 (查准率-查全率曲線)
該曲線是通過取不同的閾值下的P和R,繪制出來。這里的閾值就是指模型預測樣本為正樣本的概率。比如閾值取0.6,則所有被預測出的概率大於該閾值的樣本,都認為是被預測成了正樣本,這些被預測成正樣本的樣本中,實際是由TP(真的是正樣本)和FP(並不是正樣本)組成的。所以取一個閾值,就能計算出一組P-R,那么取多個閾值后,P-R曲線就繪制出來了。
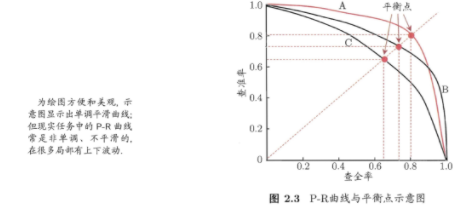
從上圖中可以看到,P-R曲線是采用平衡點(P=R的點)來判斷哪個學習器更好(圖中有A、B、C三個學習器),A好於B好於C。
- F1分數和Fβ分數
然而,上面的度量方法只能通過看圖來理解,但是我們希望能更直接的通過一個分數來判定模型的好壞。所以更常用來度量的方法是取相同閾值下各模型的F1分數或Fβ分數(以下截圖來自周志華老師的西瓜書[1]):
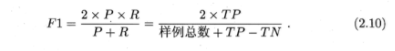
F1分數的公式是怎么來的呢?看下圖:2.10的公式,其實是由下面的調和平均公式推導出來的。

所謂調和平均數就是:所有數字的倒數求算術平均后,再取倒數。該值平均考慮了P和R的表現。
為什么β>1時查全率有更大影響,而β<1時查准率有更大影響呢?看下圖:2.11的公式,其實是由下面的加權調和平均公式推導出來的。

β的平方相當於1/R的權重,當β大於1,相當於提高1/R的重要度,當β小於1,相當於降低了1/R的重要度,而R正是查全率。
所以,當我們更傾向於查准率R的表現(即想查的更全,寧抓錯不放過)時,可以將β設置為一個大於1的數字,具體設置多少,就要看傾向程度了,然后進行Fβ分數的比較。
- ROC曲線
ROC的全稱是Receiver operating characteristic,翻譯為受試者工作特征。先不用管這個名字有多難理解。我們先弄清楚ROC曲線是什么。ROC曲線如下圖[2]:
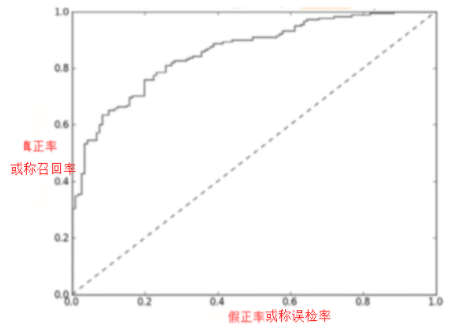
縱坐標是真正率(其實就是召回率/查全率)=TP/(TP+FN),橫坐標是假正率(誤檢率FPR)=FP/(FP+TN)。
該曲線是模型在不同閾值(與PR曲線中提到的閾值意思一樣)下的查全率和誤檢率的表現。當閾值設為0時,相當於所有樣本預測為正,查全率達到1,誤檢率當然也達到1;當閾值設為1時,相當於所有樣本預測為負,查全率達到0(太嚴格了),誤檢率當然也達到0(因為嚴格嘛)。
因為我們希望召回率高,誤檢率低,所以曲線上越接近左上角(0,1)的點表現越好。所以ROC曲線是干嘛的?就是通過查全率和誤檢率的綜合表現來評價模型的好壞用的。
你可以嘗試大量增加測試樣本的正樣本或負樣本的數量,讓數據集變的不均衡,然后會發現ROC曲線可以幾乎穩定不變,而PR曲線會發生巨大的變化。如下圖:[5]。

可以根據PR曲線中P(precision)的公式,R(recall)的公式,根據ROC曲線中R(recall)的公式,誤檢率(FPR)的公式來理解,這里不細說了。
- AUC
area under curve。定義為ROC曲線下的面積。然因為這個面積的計算比較麻煩。所以大牛們總結出了下面的等價的計算方法。
假設一組數據集中,實際有M個正樣本,N個負樣本。那么正負樣本對就有M*N種。
AUC的值等同於在這M*N種組合中,正樣本預測概率大於負樣本預測概率的組合數所占的比例。
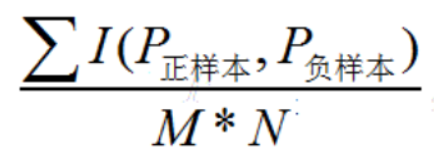
其中I函數定義如下:
P正>P負,輸出1;
P正=P負,輸出0.5;
P正<P負,輸出0。
上面的計算方法已經比計算面積要愉快多了,但是還有相對更好的計算思路:
按照預測概率從小到大排序,得到排好序的M*N個組合,其中正樣本的序號就表示比當前正樣本概率小的樣本個數,再從這些樣本中減去正樣本的個數,就得到了當前正樣本概率大於負樣本概率的組合數。
為了計算方便,我們先把排好序的M*N個組合中所有正樣本的序號累加,然后減去正樣本的個數的累加,就得到了所有正樣本概率大於負樣本概率的組合數,然后除以M*N,就得到了在這M*N種組合中,正樣本預測概率大於負樣本預測概率的組合數所占的比例,這個比例等同於AUC。下面我們來看看具體的計算公式[4] :
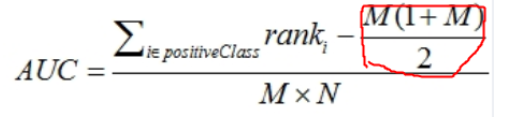
看上去挺復雜的,稍微解釋一下你就明白了。
分子左邊的部分就是排好序的M*N個組合中所有正樣本的序號累加,
分子右邊的部分其實就是正樣本的個數的累加的公式,這個稍微解釋一下:比如我們有5個正樣本,那么正樣本的個數累加就是1+2+3+4+5=15,帶入公式就是5*(1+5)/2=15,而這個公式就是“高斯等差數列求和公式”: (首項+末項)x項數÷2。
分母部分比較好理解了,就是所有的正負樣本的組合數。
如果在排序的時候遇到了概率值相同的情況,其實誰前誰后是沒有關系的,只是在累加正樣本的序號的時候,如果有正樣本的概率值和其他樣本(包括正和負)的概率值一樣,那么序號是通過這些相同概率值的樣本的序號的算術平均數來計算的。舉例如下[3]:
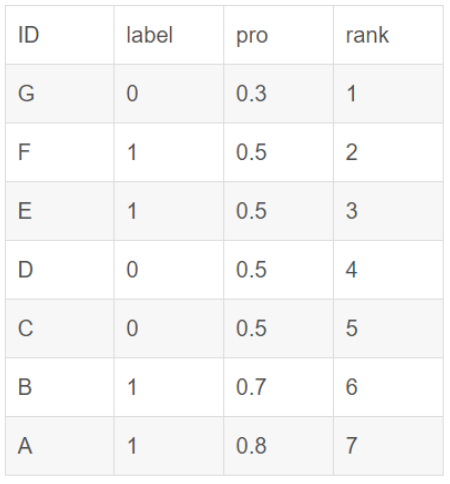
在累加正樣本的序號的時候,正樣本的rank(序號)值:
對於正樣本A,其rank值為7
對於正樣本B,其rank值為6
對於正樣本E,其rank值為(5+4+3+2)/4
對於正樣本F,其rank值為(5+4+3+2)/4
最后正樣本的序號累加計算就是:
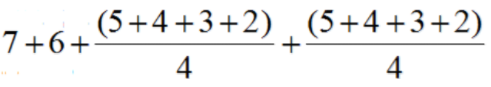
求出了各個模型的ROC曲線下的面積,也就是AUC,就可以比較模型之間的好壞啦。
注意
以上度量指標一般都是用於二元分類,如果是在多分類的場景下,可以拆成多個二分類問題來度量。而如果除了分類還有其他預測的任務,就需要針對性的度量指標來評估模型的好壞了。比如像目標檢測,除了目標分類,還要預測目標的邊界框位置,所以用的是mAP指標,具體可以參考下一篇文章《目標檢測中為什么常提到IoU和mAP,它們究竟是什么?》
參考文獻
[1]《西瓜書》周志華 著
[2]《機器學習實戰》Peter Harrington 著
[3] https://blog.csdn.net/qq_22238533/article/details/78666436
[4] https://blog.csdn.net/pzy20062141/article/details/48711355
[5] https://www.cnblogs.com/dlml/p/4403482.html
ok,本篇就這么多內容啦,感謝閱讀O(∩_∩)O,88
推薦閱讀:
還再@微信官方要國旗?這才是正確的打開方式~
