定義
余弦相似度通過測量兩個向量的夾角的余弦值來度量它們之間的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大於1;並且其最小值是-1。從而兩個向量之間的角度的余弦值確定兩個向量是否大致指向相同的方向。兩個向量有相同的指向時,余弦相似度的值為1;兩個向量夾角為90°時,余弦相似度的值為0;兩個向量指向完全相反的方向時,余弦相似度的值為-1。這結果是與向量的長度無關的,僅僅與向量的指向方向相關。余弦相似度通常用於正空間,因此給出的值為0到1之間。
注意這上下界對任何維度的向量空間中都適用,而且余弦相似性最常用於高維正空間。例如在信息檢索中,每個詞項被賦予不同的維度,而一個維度由一個向量表示,其各個維度上的值對應於該詞項在文檔中出現的頻率。余弦相似度因此可以給出兩篇文檔在其主題方面的相似度。
另外,它通常用於文本挖掘中的文件比較。此外,在數據挖掘領域中,會用到它來度量集群內部的凝聚力。
兩個向量間的余弦值可以通過使用歐幾里得點積公式求出:

給定兩個屬性向量,A和B,其余弦相似性θ由點積和向量長度給出,如下所示:
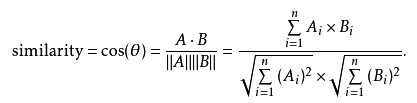
這里的Ai、Bi分別代表向量A和B的各分量。
公式推導
如果對於上述的公式不是很理解,那就請看這里的公式推導:
(由於不會鍵盤敲數軸和公式,就直接上筆了)

案例
看一個案例來加深理解:
某購物網站有如下數據:小明購買了T恤a、T恤b、T恤e,小紅購買了T恤b、T恤c、小強購買了T恤a、T恤e。
把以上信息轉為向量圖,代入上述的公式來計算得出相似度,過程如下:

由上述的結果便可得到如下結論:小明和小紅這兩個用戶有一定的相似度,但是不大,因為他們只有一個共同商品;小明和小強這兩個用戶相似度最大,因為他們有兩個共同商品;而小紅和小強的相似度為0,因為小紅買的T恤小強都沒有買。
原文鏈接:https://blog.csdn.net/smile_shujie/article/details/89516305
