There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length p, and a laser ray from the southwest corner first meets the east wall at a distance q from the 0th receptor.
Return the number of the receptor that the ray meets first. (It is guaranteed that the ray will meet a receptor eventually.)
Example 1:
Input: p = 2, q = 1
Output: 2
Explanation: The ray meets receptor 2 the first time it gets reflected back to the left wall.

Note:
1 <= p <= 10000 <= q <= p
這道題給了我們一個正方形的房間,說是四面都是鏡子牆,然后在西南角有一個激光發射器,其余三個角都有接收裝置,問我們最終激光會被哪個接收器接收。第一次讀題時這句 "Return the number of the receptor that the ray meets first." 讓博主理解錯誤了,以為是讓返回接收器的個數,以為接收器也能反射激光到其對角的接收器,那么接收器2和0互相反射,就是返回經過了2個接收器,接收器1返回到反射點,就是返回經過了1個接收點,想的是一套一套的,結果人家讓返回的是接收器的標號,個人覺得將 number 改為 index 會減少些歧義。無所謂了,反正最終搞懂了題意就行了。其實這道題的正確解法還挺難想的,因為大家很容易走進的誤區就是研究反射角啥的,然后算具體反射到了哪一個位置,再算下一個位置,其實這樣都將題目變復雜了。博主把這一類型歸為腦筋急轉彎 Brain Teaser,一般都有很巧妙的數學解法,並不需要太復雜的算法。
首先從最簡單的情況開始分析,當p和q相等的時候,那么激光直接到達接收器1,當 p/q = 2 的時候,就如例子中所示,經過右邊的鏡面反射后到達左上角的接受器2。那么我們再來考慮下這三種情況 p/q = 3, p/q = 4, p/q = 3/2,並畫出折射情況如下所示:
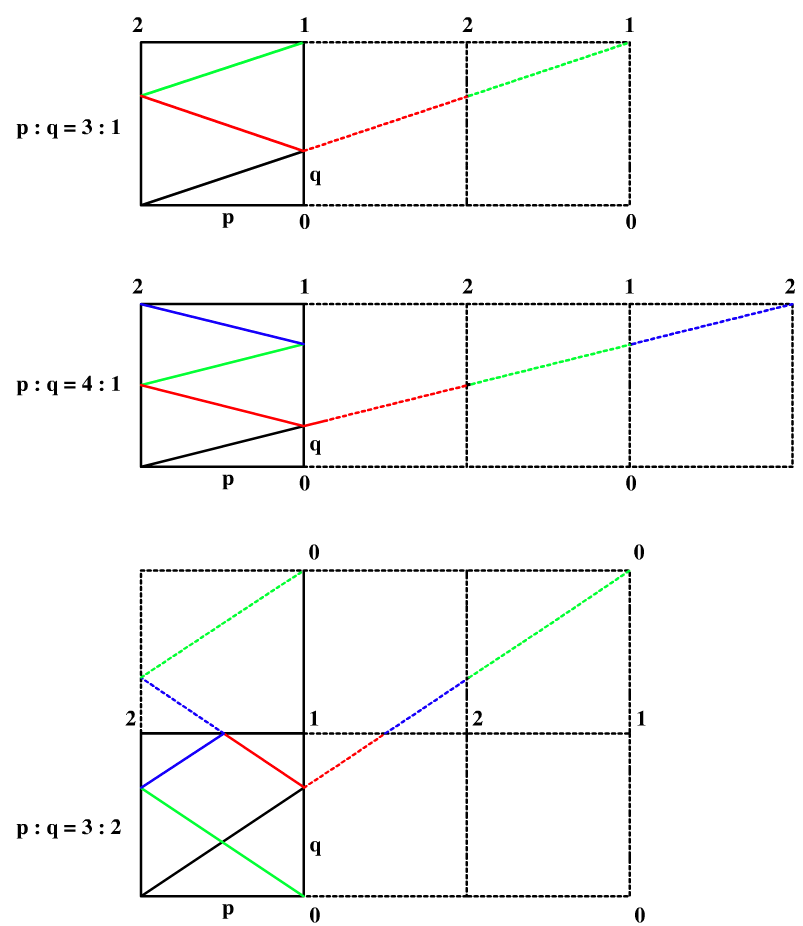
這里就有些比較好玩的規律了,我們知道激光遇到鏡面是會發生折射的,但是假如沒有鏡面,就會仍然沿直線前進,那么對於 p/q = 3 時,若我們在右邊增加大小相同的2個房間,則激光會到達右上角,由於第二個房間和原始房間是鏡面對稱的,而第三個房間和第二個房間也是鏡面對稱的,則第三個房間和原始房間就是一樣的了,那么就可以假設一下,奇數房間和原始房間的布局相同。再來看上圖中的 p/q = 4 時,我們在右邊復制了三個房間,在第四個房間的時候,激光到達了右上角,而第偶數個房間的布局是跟原始房間稱鏡面反射的,則就是接受器2了。其實有些時候,我們不止要在右邊復制房間,還需要在上面復制房間,比如當 p/q = 3/2 時,我們需要復制出一個 2x3 大小的矩陣出來,在水平方向共有三個房間,是奇數則水平方向和原始房間布局一致,但是豎直方向也復制了房間,那么豎直方向有偶數個房間,則豎直方向和原始房間成鏡面反射,則最右上角為接收器0。
分析到這里,我們應該已經能總結出規律如下了:
- p為奇數,q為奇數時,到達接收器1。
- p為奇數,q為偶數時,到達接收器0。
- p為偶數,q為奇數時,到達接收器2。
那你可能會有疑問了,為啥沒有p和q均為偶數的情況呢?比如 p = 4, q = 2,其實只要我們畫個圖就知道,這個跟 p = 2, q = 1 的情況是一摸一樣的,若p和q均為偶數,那么那么一定可以同時除以2,那么其實我們可以先對p和q進行判斷,若二者同為偶數,則同時除以2,直到不同時為偶數時,然后再帶入上面歸納的三種情況求解即可,參見代碼如下:
解法一:
class Solution {
public:
int mirrorReflection(int p, int q) {
while (p % 2 == 0 && q % 2 == 0) {
p /= 2; q /= 2;
}
if (p % 2 == 0) return 2;
if (q % 2 == 0) return 0;
return 1;
}
};
其實我們可以進一步化簡,將三種情況融為一個表達式即可,即 1 - p%2 + q%2,不信的話可以帶數字驗證一下,碉堡了有木有,參見代碼如下:
解法二:
class Solution {
public:
int mirrorReflection(int p, int q) {
while (p % 2 == 0 && q % 2 == 0) {
p /= 2; q /= 2;
}
return 1 - p % 2 + q % 2;
}
};
其實不光是p和q同時為偶數的時候可以化簡,只要p和q的最大公約數 Greatest Common Divisor 大於1時,都可以化簡,比如,若 p = 6, q = 3 時跟 p = 2, q = 1 的情況也是一樣,那我們就可以先求出p和q的最大公約數,然后用p和q分別除以這個最大公約數,再帶入上面的那個一行公式求解即可,參見代碼如下:
解法三:
class Solution {
public:
int mirrorReflection(int p, int q) {
return 1 - p / gcd(p, q) % 2 + q / gcd(p, q) % 2;
}
int gcd(int p, int q) {
return q ? gcd(q, p % q) : p;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/858
參考資料:
https://leetcode.com/problems/mirror-reflection/
[LeetCode All in One 題目講解匯總(持續更新中...)](https://www.cnblogs.com/grandyang/p/4606334.html)
