2019/3/30
二元線性回歸——矩陣公式法又名:對於python科學庫的糟心嘗試
二元線性回歸嚴格意義上其實不過是換湯不換葯,我對公式進行推導,其實也就是跟以前一樣的求偏導並使之為零,並且最終公式的嚴格推導我大概也只能說是將將理解,畢竟最初的矩陣一開始都不太清楚應該是什么樣子的,其中,Coursera的課程起到了非常顯著的幫助。
其實這個部分我並不想寫太多,因為理解並不是十分透徹,總體來講,感覺就是一個公式的事情,其中對於python數據類型以及python庫函數的使用反而耗費的時間更多,回頭來更新。
python庫函數的運用非常重要,也是卡住我好久的主要原因,其次,對於python幾種數據結構類型也讓我十分苦惱,畢竟我不太清楚大部分函數會返回給我什么樣的結果。
其中最終的公式應該說是非常普及了,隨便的搜索便可查找到,雖然花了這么大的功夫,最終帶給我的印象卻是遠遠不及梯度下降的那種循序漸進看着計算機一步步探索來的深刻。
然而,這不正是前人的努力所要想做到的一步到位的方式嗎?
雖然是真真正正的計算公式,但是若是面對特殊的矩陣情況或者過大的矩陣,這個方法也是力不從心的,詳情我不多贅述,畢竟我還是個沒有系統學習線代概率的赤腳蒟蒻。
先這樣,或許會再來更新吧。
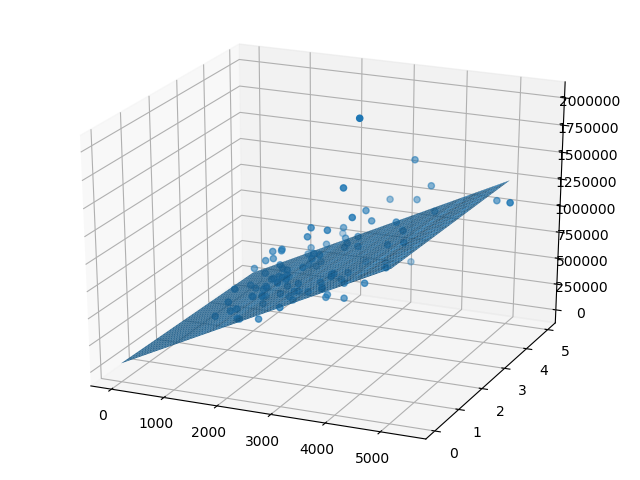
以下是利用Coursera提供的部分數據進行的實現圖像:
這里給出完整代碼:
import xlrd
import sympy as sp
import xlwt
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
workbook=xlrd.open_workbook(r'dataset.xlsx')
sheet=workbook.sheet_by_index(0)
Y1=sheet.col_values(0)
X1=sheet.col_values(1)
X2=sheet.col_values(2)
#Axes3D
fig = plt.figure()
ax = Axes3D (fig)
ax.scatter(X1, X2, Y1)
#H為100*3矩陣,讀入現有數據,第0列為1
H=[]
for i in range(100):
values=[]
values.append(1)
values.append(X1[i])
values.append(X2[i])
H.append(values)
#將H0數組化
H0 = np.array(H)
#H1為H的轉置矩陣
H1=np.array(H0).T
H2=H1@H0
#求逆矩陣
H3=np.linalg.inv(H2)
#最終結果計算
temp=H3@H1@Y1
temp=np.mat(temp)
w0=temp[0,0]
w1=temp[0,1]
w2=temp[0,2]
#生成兩坐標軸取點
x1=np.linspace(0,5000,100)
x2=np.linspace(0,5,100)
#將兩坐標軸點合成
x1, x2 = np.meshgrid(x1, x2)
#結果方程,並輸出最終結果圖
#z=w0+w1*x1+w2*x2
ax.plot_surface(x1,x2,w0+w1*x1+w2*x2)
plt.show()
