哈希表
先從數組說起
任何一個程序員,基本上對數組都不會陌生,這個最常用的數據結構,說到它的優點,最明顯的就是兩點:
- 簡單易用,數組的簡易操作甚至讓大多數程序員依賴上了它,在資源富足的情況下,我們甚至會無意識地忽略其它更適用的數據結構而使用數組(別說你沒這么干過..)。
- 查找的快速性,數組中查找元素可以直接通過下標進行定位,速度快。
我在剛開始寫程序的時候,也會經常用到數組,而且往往數組中的元素都是預定義好的,當元素少的時候,常用的做法是使用宏定義來定義下標:
#define ZHANGSAN 0
#define LISI 1
...
這樣,就可以通過ZHANGSAN這個宏定義作為下標訪問到"張三"。我們就產生了一種數組就是這么使用的錯覺。
但是,如果數組內的元素是預先不知情的,或者數量龐大呢?宏定義這種做法明顯不再合適了。
比如要存儲學生相關信息時,便使用結構體數組,在查找時就輪詢每一個結構體中"學號"字段,來判斷是否命中。在這種情況下,數組就完全失去了快速查找的優勢。
hash函數的使用
其實,在上述情況中,我們需要解決的問題就是建立 "元素和數組下標" 之間的映射關系,hash函數就擔任了這么一個角色(但是hash函數並不僅僅在hash表中使用)。
哈希函數到哈希表
hash函數,又稱為散列函數,但是這個hash函數並沒有什么統一標准,它的核心思想就是就是把任意長度的輸入(又叫做預映射pre-image)通過散列算法變換成固定長度的輸出,該輸出就是散列值。
這種轉換是一種壓縮映射,也就是,散列值的空間通常遠小於輸入的空間,不同的輸入可能會散列成相同的輸出,所以不可能從散列值來確定唯一的輸入值。
簡單的說就是一種將任意長度的消息壓縮到某一固定長度的消息摘要的函數,這個消息可能是字符、數組、字符串等等。
擁有這樣的hash存儲結構的數據結構稱為散列表,或者叫哈希表。
哈希表一般基於數組實現,特定情況下結合鏈表,但是數組是哈希表基礎數據結構。
示例
定義總是臭又長,我們來舉個例子:有100個學生,我們需要用一個容量為100的哈希表來存下他們的信息,使用他們的名字來進行hash計算,輸出0-99的下標值,我們可以這樣,我們可以嘗試定義這樣一個最簡單的hash函數:
int hash_func(char* name)
{
sum = name中每個字符值相加
return sum%100
}
這是個非常簡單的hash函數實現,每個名稱都會對應返回0-99的數組下標。
但是細心的朋友肯定能發現其中的問題:這個函數並不能保證每個name計算出來的值都不一樣,100個學生剛好填滿哈希表,而且還不考慮重名的情況,如果兩個名字計算出來的hash值相同,這就產生了沖突,畢竟一個坑只能放一個蘿卜。
很顯然,這是個"很爛"的hash函數。(事實上我們並不能撇開應用場景來單純地判斷一個hash函數的好壞,在某些情況下,線性映射能達到很好的效果,而某些情況下需要更復雜的hash函數)。
hash函數的要求
那么,一個hash函數需要滿足什么要求呢?
- 接受一個單一的參數,這個參數可以是任何類型,但是只能是一個
- 返回一個整型值(一般情況下)
- 不拋出異常
- 對於兩個相同的輸入,輸出必須相同
- 對於兩個不同的輸入,輸出相同的概率需要做到非常小。
- hash的計算不能過於復雜,時間復雜度盡可能地低。
常用的hash函數
既然自己想不到比較好的hash算法,我們就來看看別人是怎么做的吧,下面是一些常用的hash算法:
直接定址法
取key的線性函數值作為hash值,value = a * key + b,a,b為常數。這一類散列碼的特點是:對輸入為整型數據而言,不會產生下標沖突。不產生沖突當然是最完美的狀態,但是這種方式要求輸入的key遵循一定的線性規律。
除留余數法
除留余數法:假設數組的長度為l,value = key % l,這一種散列碼實現簡單,運用比較多,但是如果輸入的元素集合不具有一定的規律,比較容易產生沖突。數組的長度最好是質數,被除數為質數在一定程度上可以緩解數據堆積的問題。
數字分析法
數字分析法即對關鍵字進行分析,取關鍵字的若干位進行或者組合進行hash計算,這一類散列碼的特點是比較靈活,通常是結合其他hash函數來計算,可根據實際情況來做出調整,具有想當的靈活性。
平方取中法
取關鍵字平方后中間幾位作哈希地址。適於關鍵字長度不統一的情況,而且對於元素連續的輸入,可以很好的將其散列均勻,而且相對於除法而言,乘法的執行速度更快,這個由硬件決定。
處理沖突的方法
從hash函數的要求可以看到,事實上我們只能定義對於兩個不同的輸入,輸出相同的概率盡可能小,而不能做到完全杜絕沖突,所以我們必須提前想好處理沖突的措施。
開放定址法
開放地址法是比較常用的處理沖突算法之一,通常分為幾種:
- 線性探測:當需要插入的元素發現與已有元素下標沖突時,就依次往后遍歷,直到找到一個空槽,這時候將元素插入進去,由此可以看出,插入的操作非常簡單。
但是如果我要查找一個元素時,將Key經過hash運算之后得到的hash值作為下標找到的不一定是對應的元素(因為插入時的沖突導致往后移),這時候有幾種處理方案:
* 在只增不刪的hash表中,從計算出的hash下標處往后一個一個進行對比(對比函數就是用的key_equal()函數),直到找到元素或者找到一個空槽表示未找到,因為沖突時都是往后一個槽一個槽地找。
* 在可刪除的hash表中,刪除一個槽時,會導致中間有空槽存在,這個時候查找在插入時遇到沖突的元素的時候,最壞的情況下需要遍歷整個hash表,才能確定是否存在。或者在刪除時,將之前因沖突而放置在其他槽的元素取回,這里的操作較為復雜。
-
二次探測:在線性探測的基礎上,從依次往后遍歷變成按照 +(1²),+(2²),+(3²),+(4²)的規律進行探測,在線性探測的基礎上,可以緩解數據堆積問題,提升效率,操作上一致。
-
偽隨機數再散列:在線性探測的基礎上,將往后遍歷下標的值取一個偽隨機數,並將偽隨機數序列記錄下來,以供查找時使用。
示例
插入時解決沖突
光說不練假把式,還是得通過具體的示例才能更清楚地理解這三種處理方式:
模擬一個商場會員管理系統,目前有以下會員信息:
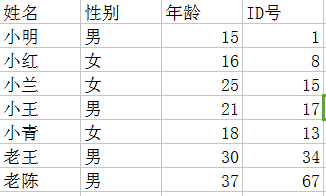
首先,我們選取ID號作為hash函數的輸入,因為可能存在重復的人名,在前期我們就應該避免會引發沖突的情況。
然后選取一個hash函數,這里我們就選擇一個簡單的除留余數法,會員目標的信息是未知的,所以得定一個比當前數據量大一些的數組,數組大小為11(實際情況要大得多,雖然這很不符合實際情況,原諒我!這只是個簡單示例!).而數組類型為結構體數組或者指針數組(數組元素都是指針,為了優化空間,當插入元素時再動態分配內存,指針放置在數組中)。
hash函數的實現如下:
int hash(int key){
return key%11;
}
好了 一切准備就緒,我們就可以開始了,為了大家的理解,我們先計算出來ID與下標的對應:

然后再一個個地插入元素,先插入小明,是這樣的:

接着插入,插入完小青之后,是這樣的:

接着插入老王和老陳,但是發現老王和老陳的hash值都是1,而且之前小明已經占了1的坑,這時候插入就要解決沖突。
線性探測解決沖突
老王需要寫入的時候,發現1已經被小明占了,沒辦法,只好往后找位置,但是又發現2號下標被小青占了,只好再往后找,發現3號位置是空的,放在3號位置。
老陳進行同樣的操作,發現234號位置都已經被占,放置在5號位置。這時候的表空間這樣的:

二次探測解決沖突
老王要寫入,1號被占用,看一下2號位置(1+1),發現被小青占了,繼續看5(1+4)號,5號為空,放置在5號。
老陳進行同樣的操作,1,2,5號被占用,再看10(1+9)號位置,10號位置為空,放置在10號。這時候的表空間是這樣的:

偽隨機再散列解決沖突
我們選取一個偽隨機序列{2,5,9},
老王要寫入,1號被占用,找到3(1+2)號,3號為空,放入3號位置。
老陳進行同樣的操作,1,3號被占用,找到6(1+5)號,6號被占用,找到10(1+9)號,放置在10號,這時候的表空間是這樣的:

實際情況是復雜多變的,博主也不指望一個簡單的示例能代表所有情況,但是從這個示例還是可以看出,對於解決沖突,線性探測容易產生堆積,而二次探測可緩解堆積現象(乘法可以將間距放大)。而對於偽隨機再散列,所產生的結果是不定的,因為誰也不知道生成的隨機序列是否合適,但是一旦數據規模增大,這種方式更有優勢,因為偽隨機同時代表着分布均勻。
查找效率
別忘了,hash表建立的目的可不是為了插入,而是為了更方便地查找使用(增刪改伴隨着查找),那這三種方式的查找效率怎么樣呢?
情況1:只支持查找、更改,不支持刪除
查找其實就是按照插入的方式進行查找,在這里我們考慮一下比較極端的情況,如果我們要查找ID為67(老陳)的信息:
線性探測:老陳的hash計算后對應1號,對比之后發現1號並不是老陳的信息,往后一個個對比,如果遍歷到空位置,表示表內沒有對應,在這里,找到5號位置時,命中。
二次探測:與線性探測一致,只是將往后逐個遍歷變成遍歷1,5,10,如果遍歷到空位置,表示表內沒有對應,在這里找到10號位置時,命中。
偽隨機再散列:同上,遍歷1,3,10,如果遍歷到空位置,表示表內沒有對應,在這里找到10號位置,命中。
(可以想一想為什么遍歷過程中遇到空位置時表示表內沒有此元素)
情況2:同時支持增刪改查
在可以刪除的情況下,就更為復雜了,如果我們刪除了ID為1(小明)的信息,這時候1號為空,查找老陳信息時就不能簡單地依據遍歷到空元素表示表內沒有此元素。如果我們要查找一個ID的信息,而這個ID並不存在於這個表內,我們得遍歷整個表才能確定.(或者可以置一些被刪除的標志位來識別,但是當刪除頻繁時加大軟件難度和出錯概率)
有一種解決方案是,當我們刪除一個元素時,將其他的沖突元素移回來,這樣就可以保持 查找時以遍歷到空元素來確定此元素不存在的屬性了。
開放定址法總結
即使沒有任何示例,從直覺上來看,上述三種方式處理沖突不夠優雅,處理方式明顯不適合大規模的數據存儲,一旦數據規模增大,散列很可能出現多次沖突的情況,查找時的往后遍歷所花費的時間是不可接受的,
同時,如果涉及到數據規模的增大,當面臨幾十上百K的數據規模時,因為數組的不可擴展性,我們在剛開始就得定義一個足夠大(在不知道具體數據規模時甚至定義一個遠大於數據規模)的數組以滿足需求,又或者涉及到動態增長,這種存儲方式對空間的浪費是非常嚴重的。
鑒於數組的不可擴展,內存連續的屬性,這種hash表並不能滿足大型數據規模的應用場景,那么有什么辦法能解決數組空間的浪費以及擴展問題呢?
說到可擴展性,當然就應該想到鏈表!!!
鏈地址法
我們都知道鏈表的缺點是查找速度慢,一般情況下需要遍歷鏈表進行查找,既然數組擁有查找速度快的優點,鏈表具有可擴展性好,空間利用率高的特點,那有沒有一種東西既有數組查找的優點,又能繼承鏈表的動態擴展性呢?
答案就是hash中的鏈地址法。
鏈地址法其實理解起來非常簡單,數組中每一個元素通常放置一個鏈表頭(也可以是棧或其他,取決於應用場景),然后將所有hash值一致的元素以節點的形式鏈接在鏈表后面,按照這種方式,上面的示例中結果是這樣的:
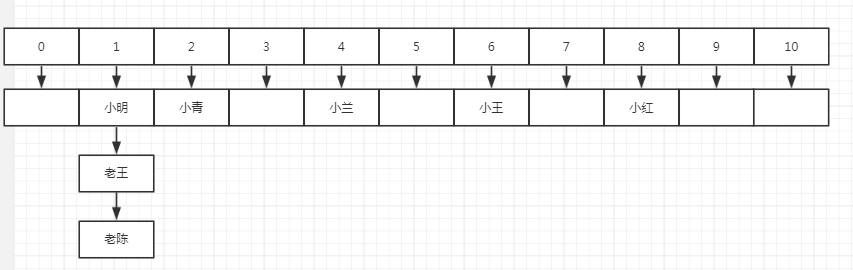
鏈地址法的優缺點
1、處理沖突簡單,平均查找時間較短。
2、相比於數組的實現,鏈地址法的擴展性明顯要更強
3、相對於開放定址法,定義的數組必須大於數據規模,容易造成浪費,而鏈地址法則不用,在一定程度上節省空間。但是開放定址法由於沖突時向后遍歷的方式,更容易將數組填滿,在這個角度上開放定址法更節省空間,所以在已知數據規模的情況下,且規模較小時,開放定址法比鏈地址法節省空間,鏈地址法的指針域同時會浪費一些空間。
4、更方便地支持增刪改查操作。
不常用的方法
再建hash
在構造hash表時同時構造多個hash函數,當發生沖突時使用下一個hash函數,直到不發生沖突。這種處理方式與開放定址法相似,但是很明顯的缺點是:在這種方式下,一旦發生沖突,將會有多次計算hash值的行為,甚至計算所帶來的時間消耗反倒遠遠超過查找本身。
建立公共溢出區
將hash表分為基本表和沖突表,當元素發生沖突時,將沖突元素放入溢出表中。但是當發生重復沖突時,就會面臨溢出區溢出的問題,這時候可能需要結合其他沖突處理方式再進行處理,如果每溢出一次,就建立一個新表,那對於空間的浪費也是不可接受的。
最好的沖突處理方式
其實最好的沖突處理方式應該是選擇一個更好的hash函數,使元素對應hash值分布更為均勻,減少沖突的存在。防范大於救火!
C++ STL中unordered container的hash實現方式
在C++ STL中,unordered_map 和 unordered_set 解決沖突的方法即為鏈地址法。
bucket
在其提供的接口函數中,將所有hash值相同的元素放入同一個bucket,bucket與上述提到的鏈表相當,在這里可以理解為一種容器。
hash_func()
unordered_map 和 unordered_set對於很多內置類型和STL 容器有默認的hash函數,但用戶也可以提供自己的hash函數。
key_equal()
如上所述,在查找時我們不能以hash值相同來判斷兩個key值相等,需要進行二次確認,即使用key_equal()函數判斷兩個key值是否完全相等。
小節
由於hash表的基礎數據結構是數組,在查找時可以直接使用下標尋址,有查找速度非常快的特點,理想中的hash表查找的時間復雜度是O(1)。
但是,相比於同樣在表單界十分受歡迎的紅黑樹而言,hash表依舊有着一些缺點:
- 不穩定,hash表極其依賴hash函數的表現,帶來的結果就是在大型應用場景需要大量的時間測試和調試。
- 占用空間較多,容易造成空間浪費。
- 紅黑樹相對來說使用簡單,不存在太多空間浪費問題,由於遵循二分查找法,在查找上的時間復雜度是O(logn),插入時最多對整棵樹調整三次,由於其綜合、穩定的性能,以及易用性,在實際應用中要比hash表受歡迎。
好了,關於hash表的討論就到此為止啦,如果朋友們對於這個有什么疑問或者發現有文章中有什么錯誤,歡迎留言
原創博客,轉載請注明出處!
祝各位早日實現項目叢中過,bug不沾身.
