[ZJOI2018]保鏢
Tags:題解
題意
鏈接
初始在平面上有一些點,九條可憐隨機出現在一個矩形內的任意一點。若九條可憐出現在\(O\)點,則平面上所有的點都從\(P_i\)移動到\(P'_i\),使得\(P'_i\)在射線\(OP_i\)上,且滿足\(|OP_i|*|OP'_i|=1\)。現在給定矩形范圍,求這些點移動后所構成的凸包的期望點數。
\(n\le 2000,x,y\le 10^5\),精度要求絕對誤差或相對誤差不超過\(10^{-7}\)。
題解
前言
神仙不可做題終於被杠下來了!撒花!
不得不說九老師這個多合一是出的真的牛逼!(比lalaxu不知道高明到哪里去了)
首先感謝Ez3real的代碼框架(不過LOJ兩人AC代碼一樣什么鬼)和yuhaoxiang的題解(這個網站很慢)。
Part 1 前置知識:圓與矩形的面積交
在計算幾何基礎里有。
Part 2 前置知識:三維凸包
在三維凸包里有。
Part 3 前置知識:歐拉公式
在Pick定理、歐拉公式和圓的反演里有。
Part 4 前置知識:反演
這道題顯然是要求平面上的點關於\(O\)的、以\(1\)為反演冪(反演半徑)的反形的凸包期望點數。
至於反演是什么可以看這個:Pick定理、歐拉公式和圓的反演
Part 5 前置知識:Voronoi圖
又稱泰森多邊形。
大概就是一個平面划分,平面上的每個點划分到離它最近的關鍵點上。
Wiki有張十分形象的圖

Part 6 前置知識:Delaunay三角剖分
三角剖分
感性理解一下就是

Delaunay三角剖分是一種有着優秀性質的三角剖分。
定理:對於任何一種三角剖分,三角形個數和外圍凸包點數之和為2n-2。
這里凸包是嚴格凸的,也就是沒有三點共線情況。
考慮用歐拉公式證明:設凸包上的點數為\(k\),三角形個數為\(F-1\),則有
#### **立體Delaunay三角剖分** 當然我們目前只考慮平面的Delaunay三角剖分,至於立體的可以看看這張圖,本文不會涉及。  (圖片來源於網絡)
#### **Delaunay三角剖分和泰森多邊形** Delaunay三角剖分和泰森多邊形是對偶圖。 對偶圖是什么呢,看下面的構造方法: 泰森多邊形的交點一般屬於三個區域,將這三個區域的標志點連起來,就得到了一個原圖的三角剖分。 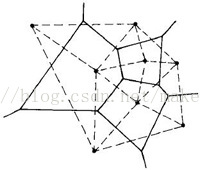 (圖片來源於網絡) 上圖中,實線是泰森多邊形,虛線鏈接,得到標志點的一個Delaunay三角剖分。
#### **Delaunay三角剖分的性質** 由於其美妙的構造,可以得到一些美妙的性質:
- 平面上的點集有且僅有唯一的Delaunay三角剖分(除出現四點共圓的情況,這時泰森多邊形有頂點屬於四個區域)。
- 任意一個Delaunay三角形的外接圓不包含點集中的其他點。(稱為Delaunay三角形的空圓性質)。
- Delaunay三角剖分相比其他的三角剖分,所有三角形的最小角最大
#### **Delaunay三角剖分的構造** 以下內容摘自百度百科 **Bowyer-Watson算法**
- 構造超級三角形(類似半平面交中的超級平面)。
- 插入點\(P\),找到點\(P\)的影響三角形(外接圓包括點\(P\)的三角形),刪除影響三角形的公共邊,並把\(P\)向這些影響到的點連邊。
- 對原圖進行優化
- 重復\(2\)直到所有點插入完畢
步驟2圖示:

步驟3圖示:轉變連接對角線的方式使其滿足空圓性質

和求三維凸包類似的復雜度分析,復雜度大概是\(\cal O(n^2)\)
Part 7 初步轉化
凸包點數,只能整體地去求,由於三角剖分的定理,我們可以轉而求三角剖分的三角形個數。
三角形個數是可以用期望算的。
每一個Delaunay三角形對應一個外接圓,我們稱為Delaunay圓。所以題目又轉化為算Delaunay圓的期望個數。若Delaunay圓的期望個數為\(num\),答案就是\(Ans=2n-2-num\)。
定義支配圓為包含點集中所有點的圓。Delaunay圓內不包含除Delaunay三角形三個頂點外的其他任何點,所以支配圓與Delaunay圓恰好相反。
則以下結論成立
- 對於Delaunay圓,若反演中心在圓內,其反形是支配圓;否則反形還是Delaunay圓。
- 對於支配圓,若反演中心在圓內,其反形是Delaunay圓;否則反形還是支配圓。
這題不用考慮反演中心在圓周上的情況(概率為0)
這里有yuhaoxiang大佬做的一個Geogebra演示文件,我把兩種情況截圖下來是這樣的:
Delaunay圓,反演中心在圓內,反形是支配圓

Delaunay圓,反演中心在遠外,反形還是Delaunay圓

題目轉化為:求原圖中Delaunay圓的個數×反演中心在圓內的概率+支配圓的個數×反演中心在圓外的概率
若其期望為\(E\),則\(Ans=2n-2-\)反形是Delaunay圓的概率\(=2+E\)
(這句話看完\(Part 8\)再回來看)對於這\(n\)個點,每個點一定至少會是一個Delaunay圓對應的其中一個頂點,所以這\(n\)個點每個點都會出現在凸包上,則凸包一共有\(2n-4\)個面,所以Delaunay圓+支配圓\(=2n-4\)。
Part 8 進一步轉化
考慮圓的方程$$x^2+y^2+Dx+Ey+F=0$$若令\(z=x^2+y^2\),可以得到\(Dx+Ey+z+F=0\),這是空間坐標系中的一個平面方程
\(z=x^2+y^2\)長這樣:
例如圓\((x-1)^2+(y-1)^2=1\)可以表示為\(-2x-2y+z+1=0\),長這樣:
自己做了一個動畫:網址。
那么如果一個點\((x,y)\)在圓上,則\((x,y,x^2+y^2)\)在該圓對應的平面上
同理,在圓外或圓內,對應着在平面的一側。具體來說,在其平面上面表示在圓外,在平面下面表示在圓內。
於是,把所有點映射到三維坐標系中,求凸包,下凸面對應Delaunay圓,上凸面對應支配圓。
Part 9 實現過程
首先讀入所有的點並進行隨機微小擾動,使得不存在多點共圓以及最后求出三維凸包中不存在與\(z \)軸平行的凸面。
然后求解三維凸包,這里采用的是增量法。
對於每個凸面,得到對應的三個點、求出其外接圓。
- 如果其為上凸面,則其為支配圓,只有在反演中心在圓外,貢獻答案
- 如果其為下凸面,則其為Delaunay圓,只有反演中心在圓內,貢獻答案
那么就是算給定矩形和圓形的面積交,這個在前置知識\(Part 1\)里啦
Part 10 總結&代碼
寫了一年終於寫完了!
完結撒花!!
這題考場上一定要果斷丟,沒有部分分。
這題出得很好,考察知識點全面。很巧妙的地方是:巧妙地把圓轉化成三維空間的平面,從而把平面問題轉化為三維凸包問題。巧妙地運用三角剖分,把求凸包頂點期望個數變為求圓的期望個數。
不得不說,orz jiry!!!
Code
#include<iostream>
#include<cmath>
#define db __float128
#define orzjiry_2 19491001
using namespace std;
const db eps=1e-10;
db Rand() {return 1.0*rand()/RAND_MAX;}
int sign(db x) {return x<-eps?-1:(x>eps);}
struct v2
{
db x,y;
v2 operator + (v2 a) {return (v2){x+a.x,y+a.y};}
v2 operator - (v2 a) {return (v2){x-a.x,y-a.y};}
v2 operator / (db t) {return (v2){x/t,y/t};}
v2 operator ^ (db t) {return (v2){x*t,y*t};}
db operator * (v2 a) {return x*a.y-y*a.x;}
db operator & (v2 a) {return x*a.x+y*a.y;}
db dis() {return sqrt((double)(x*x+y*y));}
db dis2() {return x*x+y*y;}
void rot() {db t=x;x=-y;y=t;}
}jir[4];
struct v3
{
db x,y,z;
v3 operator + (v3 a) {return (v3){x+a.x,y+a.y,z+a.z};}
v3 operator - (v3 a) {return (v3){x-a.x,y-a.y,z-a.z};}
v3 operator * (v3 a) {return (v3){y*a.z-z*a.y,z*a.x-x*a.z,x*a.y-y*a.x};}
db operator & (v3 a) {return x*a.x+y*a.y+z*a.z;}
void shake() {x+=Rand()*1e-10,y+=Rand()*1e-10,z+=Rand()*1e-10;}
}P[2100];
struct Face
{
int v[3];
v3 Normal() {return (P[v[1]]-P[v[0]])*(P[v[2]]-P[v[0]]);}
}F[8100],C[8100];
int n,cnt;
namespace TAT2D
{
v2 Cross(v2 a1,v2 a2,v2 b1,v2 b2)
{
v2 a=a2-a1,b=b2-b1,c=b1-a1;
db t=(b*c)/(b*a);
return a1+(a^t);
}
int cmp(db a,db b) {return sign(a-b);}
db rad(v2 p1,v2 p2) {return atan2(double(p1*p2),double(p1&p2));}
db Calc(db r,v2 p1,v2 p2)
{
v2 e=(p1-p2)/(p1-p2).dis(),e1=e;e.rot();
v2 mid=Cross(p1,p2,(v2){0,0},e),d1=mid;
if(d1.dis()>r) return r*r*rad(p1,p2)/2;
db d=sqrt(double(r*r-d1.dis2()));
v2 w1=mid+(e1^d),w2=mid-(e1^d);
int b1=cmp(p1.dis2(),r*r)==1,b2=cmp(p2.dis2(),r*r)==1;
if(b1&&b2)
{
if(sign((p1-w1)&(p2-w1))<=0)
return r*r*(rad(p1,w1)+rad(w2,p2))/2+(w1*w2)/2;
else return r*r*rad(p1,p2)/2;
}
if(b1) return (r*r*rad(p1,w1)+w1*p2)/2;
if(b2) return (p1*w2+r*r*rad(w2,p2))/2;
return p1*p2/2;
}
db intersect(v2 O,db r)
{
db res=0;
for(int i=0;i<4;i++)
res+=Calc(r,jir[i]-O,jir[(i+1)%4]-O);
return res;
}
}
namespace TAT3D
{
bool vis[2100][2100];
int see(Face a,v3 b) {return ((b-P[a.v[0]])&a.Normal())>0;}
void Convex()
{
for(int i=0;i<n;i++) P[i].shake();
int cc=-1;cnt=-1;
F[++cnt]=(Face){0,1,2};
F[++cnt]=(Face){2,1,0};
for(int i=3;i<n;i++)
{
for(int j=0,v;j<=cnt;j++)
{
if(!(v=see(F[j],P[i]))) C[++cc]=F[j];
for(int k=0;k<3;k++) vis[F[j].v[k]][F[j].v[(k+1)%3]]=v;
}
for(int j=0;j<=cnt;j++)
for(int k=0;k<3;k++)
{
int x=F[j].v[k],y=F[j].v[(k+1)%3];
if(vis[x][y]&&!vis[y][x]) C[++cc]=(Face){x,y,i};
}
for(int j=0;j<=cc;j++) F[j]=C[j];
cnt=cc;cc=-1;
}
}
}
int main()
{
//Part 1 輸入以及初步轉化
srand(orzjiry_2);
double xx,yy;
cin>>n>>xx>>yy;jir[0]=(v2){xx,yy};
cin>> xx>>yy;jir[2]=(v2){xx,yy};
jir[1]=(v2){jir[2].x,jir[0].y};
jir[3]=(v2){jir[0].x,jir[2].y};
db S=(jir[2].x-jir[0].x)*(jir[2].y-jir[0].y),Ans=0;
for(int i=0;i<n;i++)
{
double x,y;cin>>x>>y;
P[i]=(v3){x,y,x*x+y*y};
}
//Part 2 計算三維凸包並求出反演后支配圓的期望數量
TAT3D::Convex();
for(int i=0;i<=cnt;i++)
{
v3 o=F[i].Normal();
v2 a1=(v2){P[F[i].v[0]].x,P[F[i].v[0]].y};
v2 a2=(v2){P[F[i].v[1]].x,P[F[i].v[1]].y};
v2 c=(a1+a2)/2.0,d=a2-a1;d.rot();
a1=c;a2=c+d;
v2 b1=(v2){P[F[i].v[1]].x,P[F[i].v[1]].y};
v2 b2=(v2){P[F[i].v[2]].x,P[F[i].v[2]].y};
c=(b1+b2)/2.0,d=b2-b1;d.rot();
b1=c;b2=c+d;
v2 O=TAT2D::Cross(a1,a2,b1,b2);
d=(v2){P[F[i].v[0]].x,P[F[i].v[0]].y};
db r=(O-d).dis();
if(o.z>0) Ans+=S-TAT2D::intersect(O,r);
else Ans+=TAT2D::intersect(O,r);
}
printf("%.11f\n",(double)(Ans/S+2));
}
