前言:本文解決的問題
- 什么是紅黑樹
- 什么時候使用紅黑樹
- 紅黑樹插入元素時如何保持平衡
1 什么是紅黑樹
紅黑樹(Black red Tree) 是一棵自平衡樹,每個節點都遵循以下四條:
- 所有節點只能是紅色或者黑絲
- 根節點是黑色
- 只存在相鄰的紅色節點(即紅色節點不能有紅色的父節點或者紅色的孩子)
- 任意從root到Nil節點,經過的路徑中黑色節點的數目是一樣的。
具體可以見下圖

2 什么時候用紅黑樹
2.1 為什么會提出紅黑樹
我們知道,一般在平衡二叉樹(BST)作插入、刪除、更新、查找的時間復雜度是O(log n),但是對於那種變形的BST(往一邊偏的,變成線性的)時間復雜度就會變成O(n)。紅黑樹提供了為插入刪除提供了最壞的時間保證2O(log n) ,因為它可以保持自平衡,總能把高度維持在 2log(n+1) (n為節點數目)。
2.1 什么時候用紅黑樹
相比AVL樹而言,紅黑樹沒有嚴格定義左右子樹高度差值,並不嚴格意義的平衡。如果要涉及到很多插入、刪除,用AVL的話會很多次旋轉(rotation),此時紅黑樹是更好的選擇。反之,查詢多,更改少,即靜態的話AVL是更好的選擇。在查詢效率上,由於AVL樹嚴格平衡,AVL樹會比紅黑樹略快,但時間復雜度是要給數量級上的。此外,相比較AVL樹而言,紅黑樹需要額外的O(n)的空間來存儲顏色。
在java集合框架中TreeSet和TreeMap是用紅黑樹實現的。
# 3 紅黑樹的插入 ## 3.1 插入情況分類 放方便后續說明,假設要插入的節點為Z,插入后Z的父節點為,Z.parent;Z父節點的兄弟為Z.uncle
* Case 1插入后Z本身就是根元素  如上圖所示,插入后就只有這個一個元素,此時直接把該節點變為黑色即可。
* Case 2 插入后Z的父節點是黑色(Z.parent = black ) 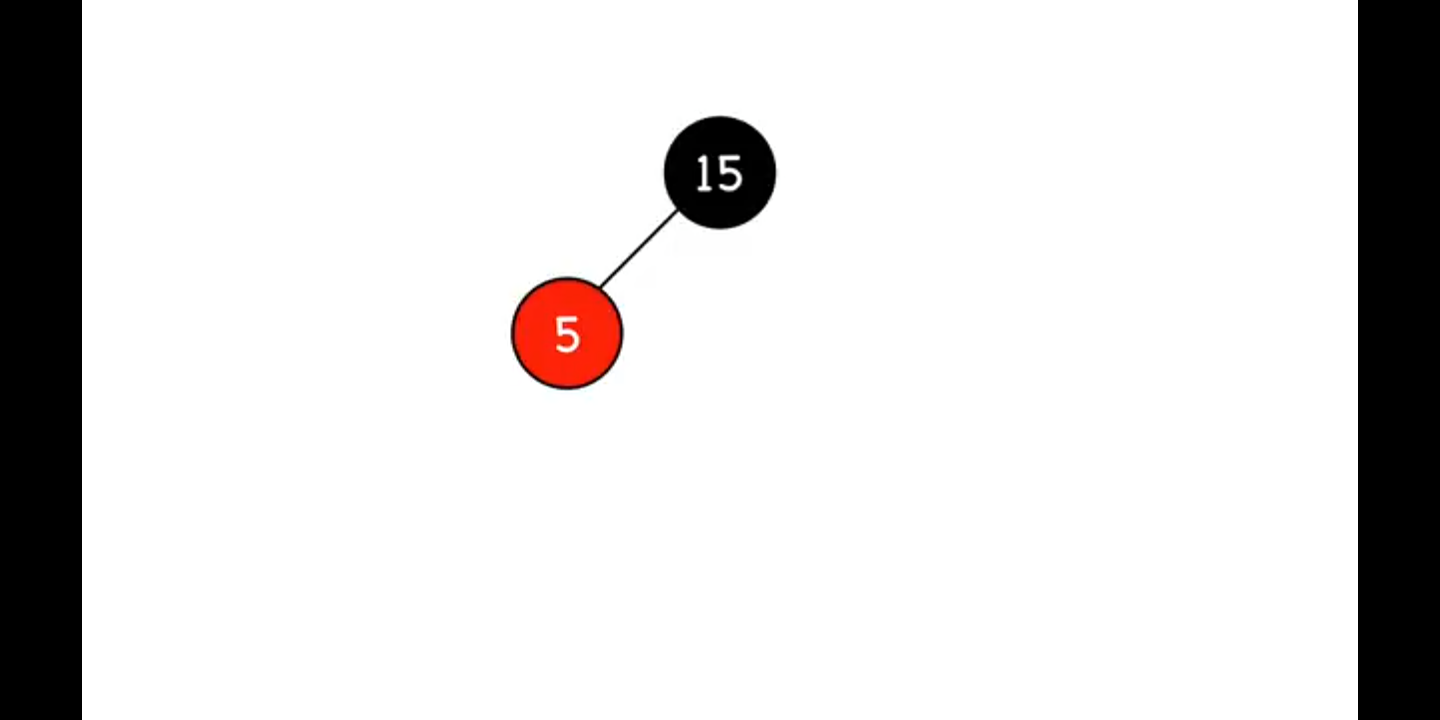 這種完全符合紅黑樹的特性,不需要做出更改
* Case 3 Z的父節點和叔叔節點都是紅色(Z.uncle and parent = red/recolor) 這種違反了紅黑樹的第三代你特征,即不存在父子節點都是紅色的,只需要把父節點和叔叔節點都變成黑色(Z.parent = black; Z.uncle = black),同時上面根節點顏色變成紅色。
* Case 4 .Z的父節點是紅色,叔叔節點是黑色,Z與父節點和祖父節之間是RL或者LR的情況。(即Z.parent = black and uncle = black(triangle) ->rotate.Z.parent) 和第三種一樣違反了父子節點都是紅色的特性。此時需要作的是把RL或者LR旋轉變成LL或者RR情況的,具體做法就說旋轉Z.parent.
* Case 5 Z的父節點紅色,叔叔節點是黑色的,Z與父節點、祖父節點在一條線上,即LL和RR的情況。(Z.uncle = black(line)->rotate.Z.grandparent &&recolor) 旋轉Z的祖父節點,並重新着色,使滿足紅黑樹特性。 
##3.2 實際舉例(針對case3、case4和case5分別舉例)
下圖中10是要加入的節點,初始樹如下 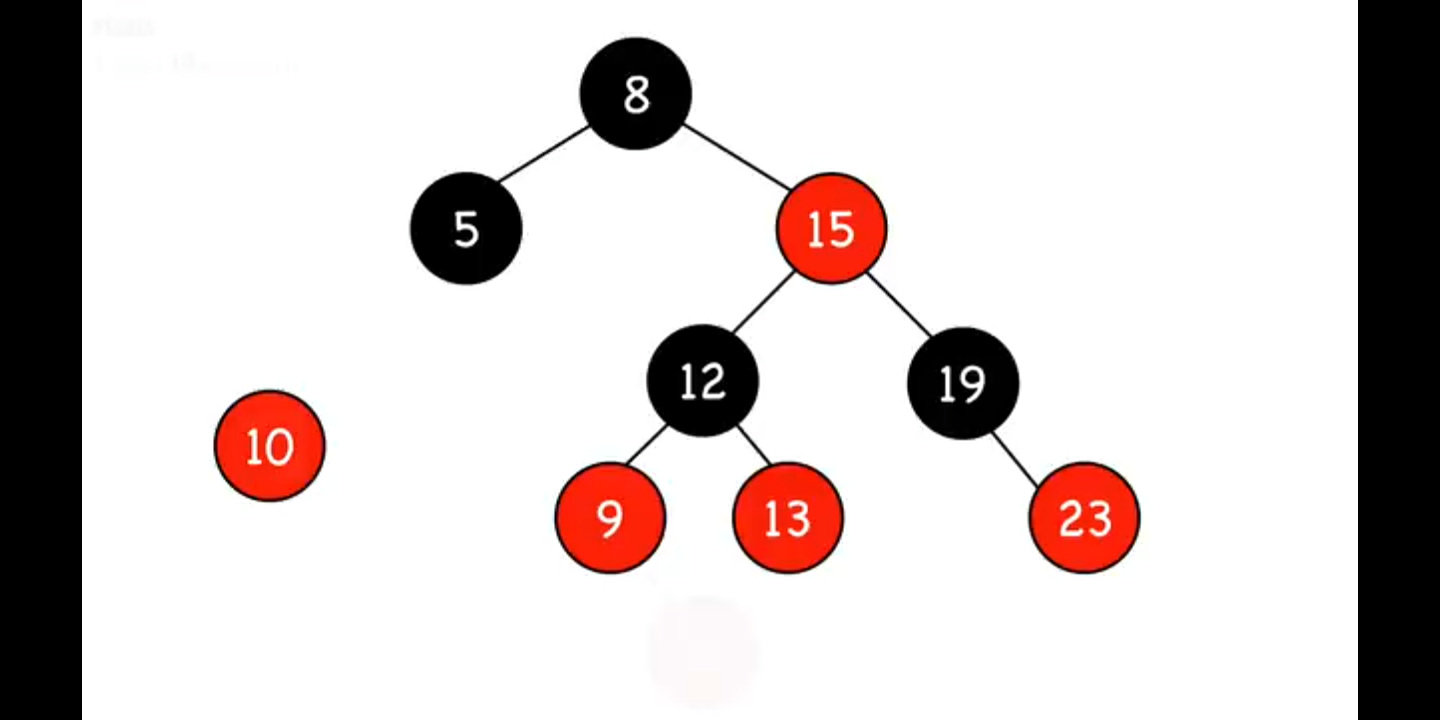
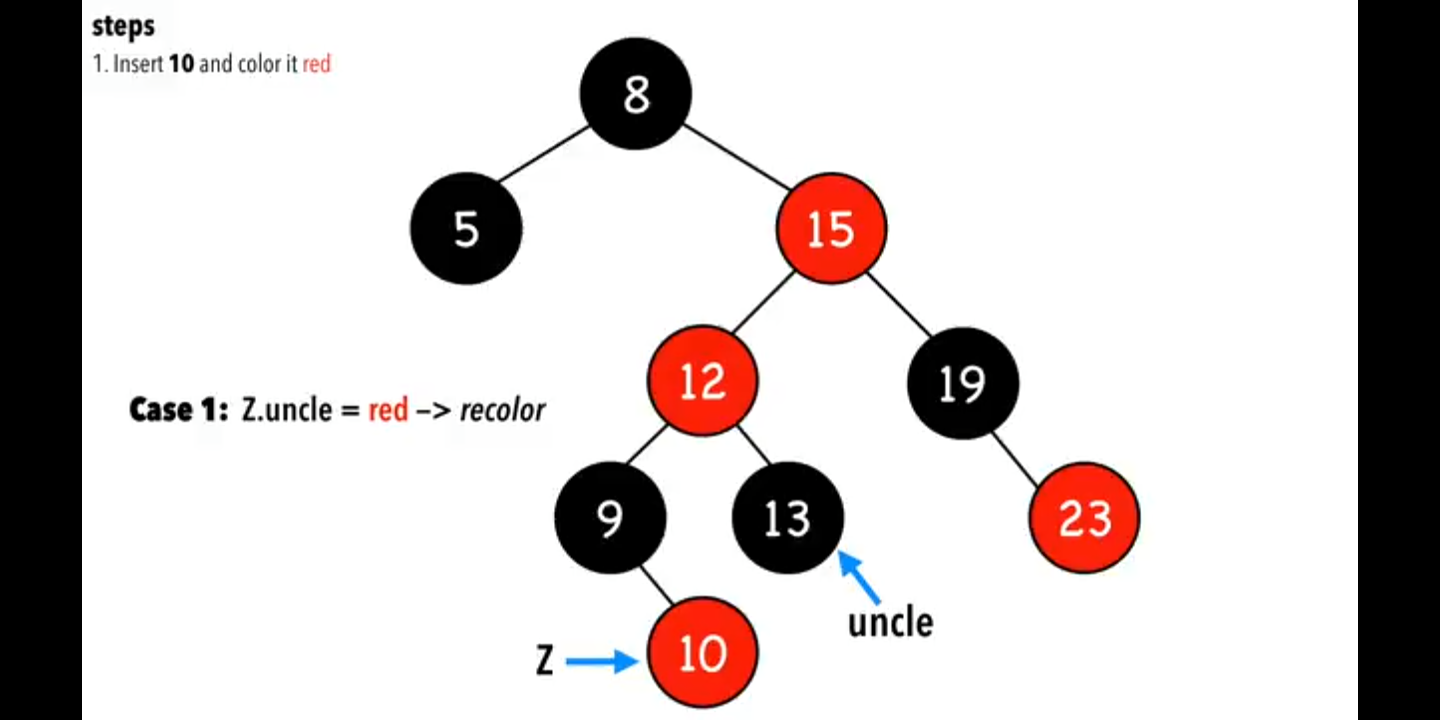
### case 3,父親和叔叔節點都是紅色的 把10加在末尾,塗紅色  把Z.parent 變成黑色,Z.uncle變成黑色,為維持從上往下的路徑中黑色節點數量不變,需要把Z.grandparent=red
### case 3,叔叔節點黑色,而且是三角形的,如圖 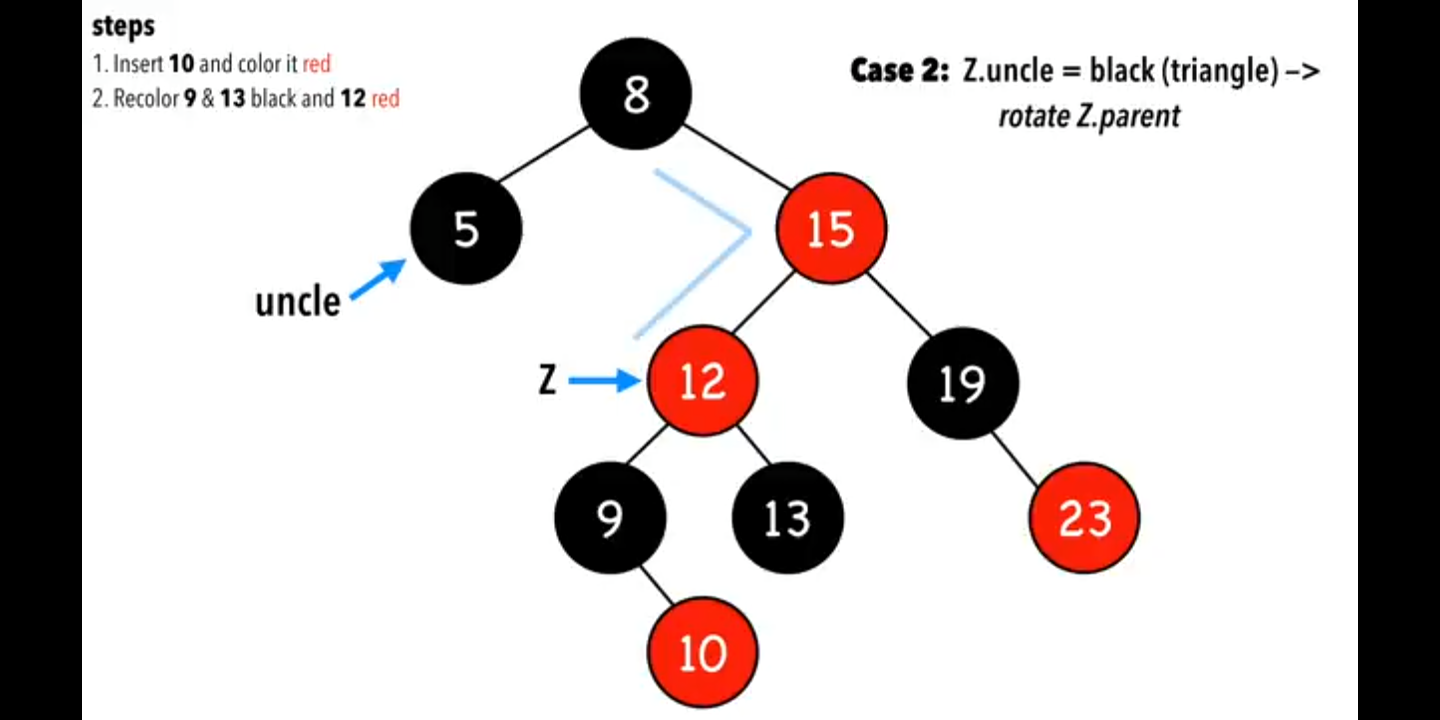
把Z.parent旋轉 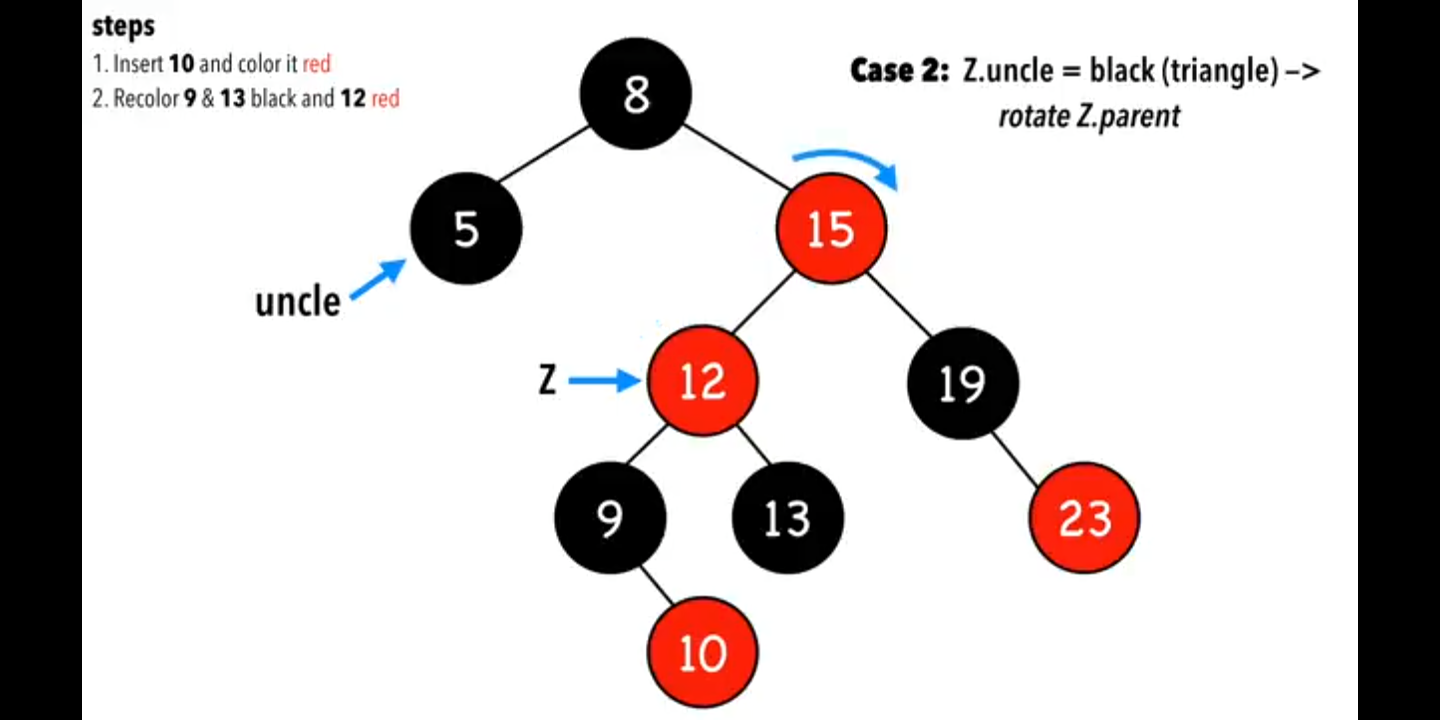
結果如下 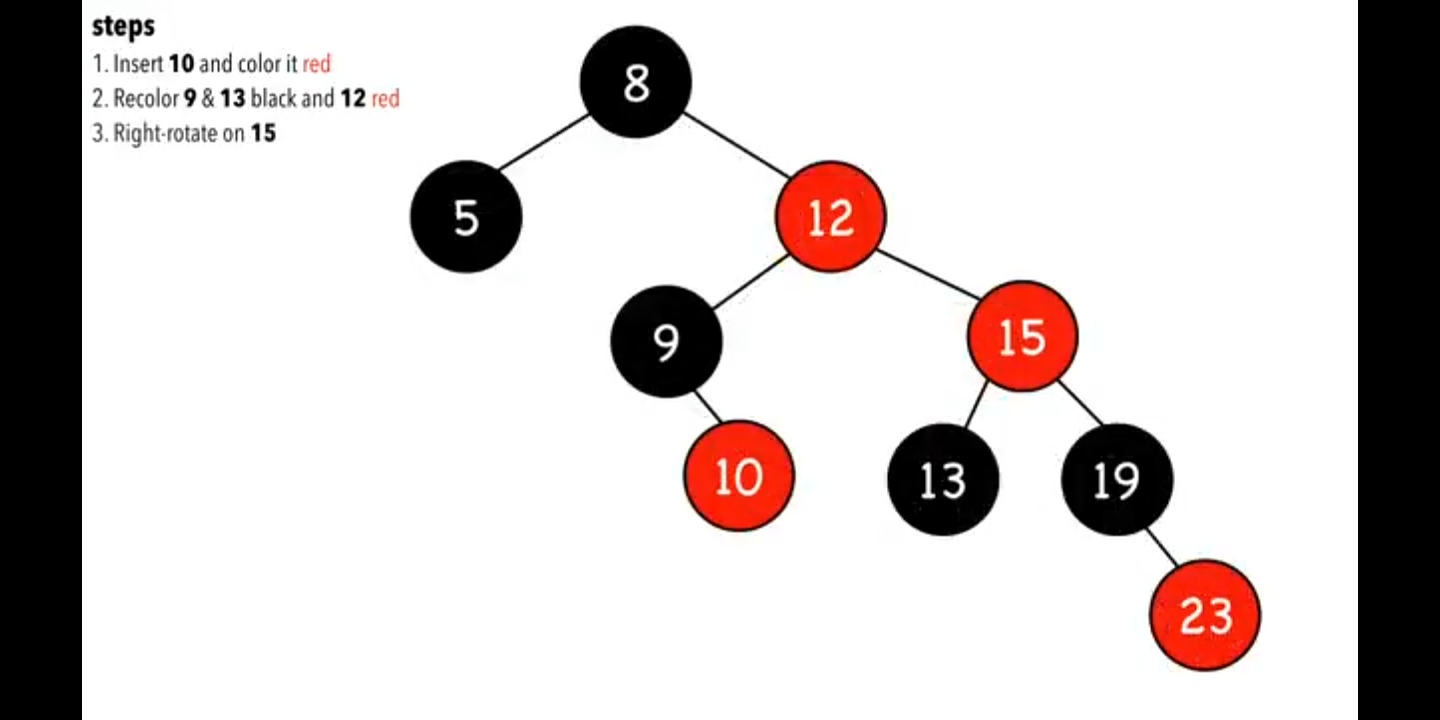
### case 5,叔叔節點黑色,而且是線性的,如圖 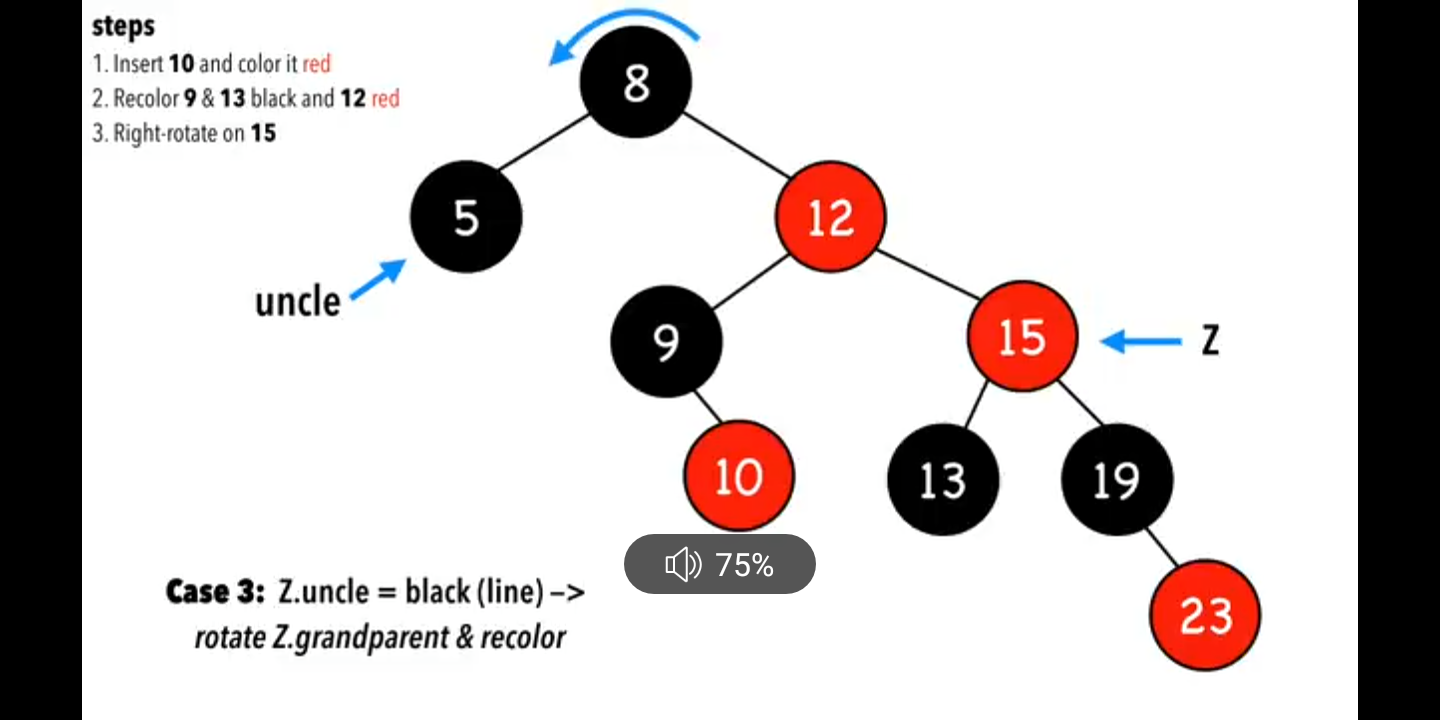
旋轉Z的祖父節點,rotate the Z.grandparent,如圖: 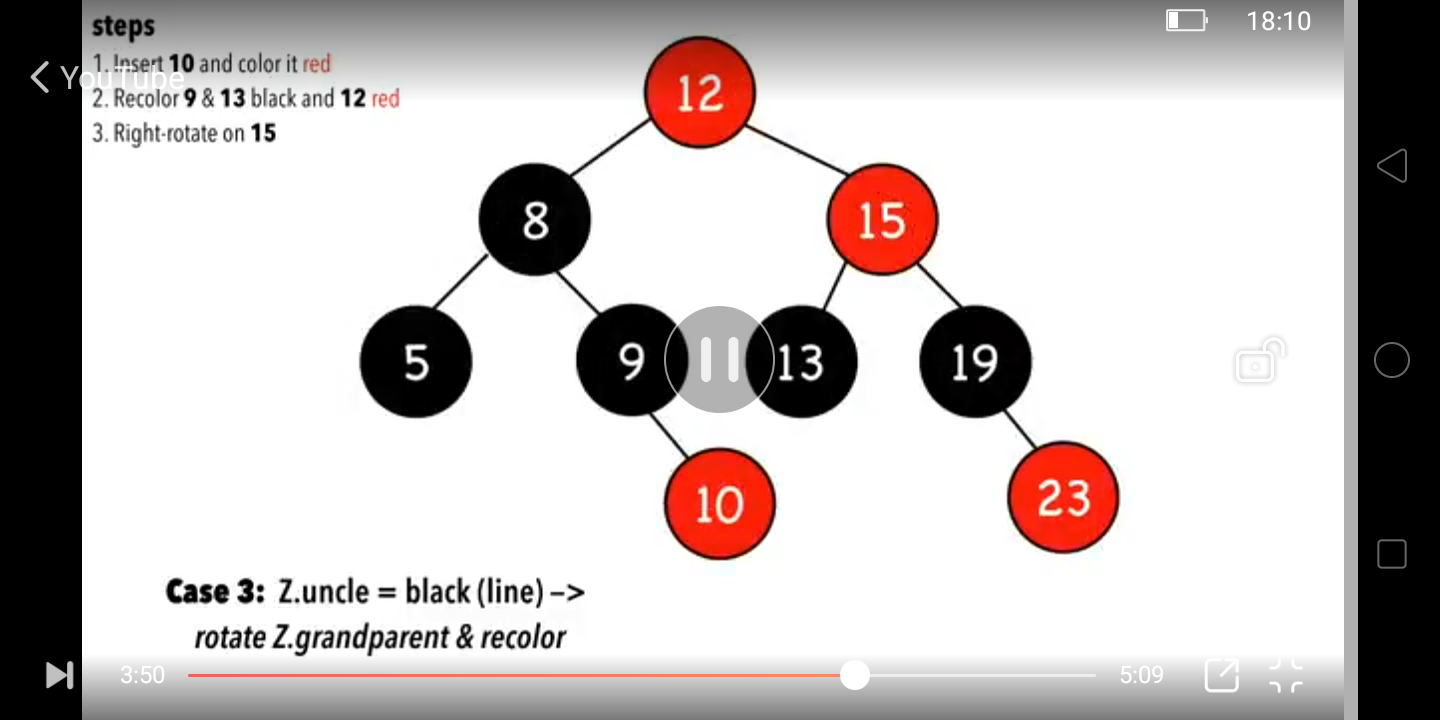
把旋轉后的重新着色

4總結
紅黑樹的插入元素,總的來說分兩部,先旋轉,再着色。旋轉把RL和LR型變成RR或者LL型,然后再旋轉上一級元素;着色要滿足紅黑樹的特性
