1. 什么是激活函數
在神經網絡中,我們經常可以看到對於某一個隱藏層的節點,該節點的激活值計算一般分為兩步:
(1)輸入該節點的值為 $ x_1,x_2 $ 時,在進入這個隱藏節點后,會先進行一個線性變換,計算出值 $ z^{[1]} = w_1 x_1 + w_2 x_2 + b^{[1]} = W^{[1]} x + b^{[1]} $ ,上標 $ 1 $ 表示第 $ 1 $ 層隱藏層。
(2)再進行一個非線性變換,也就是經過非線性激活函數,計算出該節點的輸出值(激活值) $ a^{(1)} = g(z^{(1)}) $ ,其中 $ g(z) $ 為非線性函數。

2. 常用的激活函數
在深度學習中,常用的激活函數主要有:sigmoid函數,tanh函數,ReLU函數。下面我們將一一介紹。
2.1 sigmoid函數
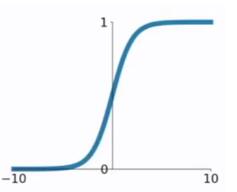
在邏輯回歸中我們介紹過sigmoid函數,該函數是將取值為 $ (-\infty, +\infty) $ 的數映射到 $ (0,1) $ 之間。sigmoid函數的公式以及圖形如下:
\[g(z) = \frac{1}{1+e^{-z}} \]
對於sigmoid函數的**求導推導**為:
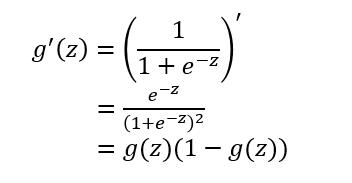
sigmoid函數作為非線性激活函數,但是其並不被經常使用,它具有以下幾個**缺點**: (1)當 $ z $ 值**非常大**或者**非常小**時,通過上圖我們可以看到,sigmoid函數的**導數** $ g'(z) $ 將接近 $ 0 $ 。這會導致權重 $ W $ 的**梯度**將接近 $ 0 $ ,使得**梯度更新十分緩慢**,即**梯度消失**。下面我們舉例來說明一下,假設我們使用如下一個只有一層隱藏層的簡單網絡:
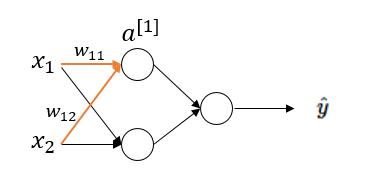
對於隱藏層第一個節點進行計算,假設該點實際值為 $ a $ ,激活值為 $ a^{[1]} $ 。於是在這個節點處的代價函數為(以一個樣本為例): $$ J^{[1]}(W) = \frac{1}{2} (a^{[1]}-a)^2 $$ 而激活值 $ a^{[1]} $ 的計算過程為: $$ z^{[1]} = w_{11}x_1 + w_{12}x_2 + b^{[1]} $$ $$ a^{[1]} = g(z^{[1]}) $$ 於是對權重 $ w_{11} $ 求梯度為: $$ \frac{\Delta J^{[1]}(W)}{\Delta w_{11}} = (a^{[1]} - a) \cdot (a^{[1]})' = (a^{[1]} - a) \cdot g'(z^{[1]}) \cdot x_1 $$ 由於 $ g'(z^{[1]}) =g(z^{[1]})(1-g(z^{[1]})) $ ,當 $ z^{[1]} $ **非常大**時,$ g(z^{[1]}) \approx 1 ,1-g(z^{[1]}) \approx 0 $ 因此, $ g'(z^{[1]}) \approx 0 , \frac{\Delta J^{[1]}(W)}{\Delta w_{11}} \approx 0 $。當 $ z^{[1]} $ **非常小**時,$ g(z^{[1]}) \approx 0 $ ,亦同理。(本文只從一個隱藏節點推導,讀者可從網絡的輸出開始,利用反向傳播推導) (2)**函數的輸出不是以0為均值**,將不便於下層的計算,具體可參考**引用1**中的課程。 **sigmoid函數可用在網絡最后一層,作為輸出層進行二分類**,盡量不要使用在隱藏層。
### 2.2 tanh函數 tanh函數相較於sigmoid函數要常見一些,該函數是將取值為 $ (-\infty, +\infty) $ 的數映射到 $ (-1,1) $ 之間,其公式與圖形為: $$ g(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}} $$
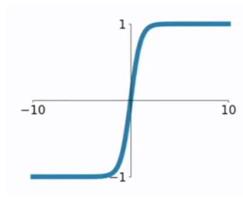
tanh函數在 $ 0 $ 附近很短一段區域內可看做線性的。由於tanh函數**均值**為 $ 0 $ ,因此彌補了sigmoid函數均值為 $ 0.5 $ 的缺點。 對於tanh函數的**求導推導**為:
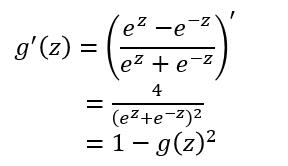
tanh函數的**缺點**同sigmoid函數的第一個缺點一樣,當 $ z $ **很大或很小**時,$ g'(z) $ 接近於 $ 0 $ ,會導致梯度很小,權重更新非常緩慢,即**梯度消失問題**。
### 2.3 ReLU函數 ReLU函數又稱為**修正線性單元(Rectified Linear Unit)**,是一種分段線性函數,其彌補了sigmoid函數以及tanh函數的**梯度消失問題**。ReLU函數的公式以及圖形如下: $$ g(z)= \begin{cases} z, & \text {if $z>0$ } \\ 0, & \text{if $z<0$} \end{cases} $$

對於ReLU函數的**求導**為: $$ g'(z)= \begin{cases} 1, & \text {if $z>0$ } \\ 0, & \text{if $z<0$} \end{cases} $$ ReLU函數的**優點**: (1)在輸入為正數的時候(對於大多數輸入 $ z $ 空間來說),不存在梯度消失問題。 (2) 計算速度要快很多。ReLU函數只有線性關系,不管是前向傳播還是反向傳播,都比sigmod和tanh要快很多。(sigmod和tanh要計算指數,計算速度會比較慢) ReLU函數的**缺點**: (1)當輸入為負時,梯度為0,會產生梯度消失問題。
### 2.4 Leaky ReLU函數 這是一種對ReLU函數改進的函數,又稱為PReLU函數,但其並不常用。其公式與圖形如下: $$ g(z)= \begin{cases} z, & \text {if $z>0$ } \\ az, & \text{if $z<0$} \end{cases} $$

其中 $ a $ 取值在 $ (0,1) $ 之間。 Leaky ReLU函數的**導數**為: $$ g(z)= \begin{cases} 1, & \text {if $z>0$ } \\ a, & \text{if $z<0$} \end{cases} $$ Leaky ReLU函數解決了ReLU函數在輸入為負的情況下產生的**梯度消失問題**。
3. 為什么要用非線性激活函數?
我們以這樣一個例子進行理解。
假設下圖中的隱藏層使用的為線性激活函數(恆等激活函數),也就是說 $ g(z) = z $ 。

於是我們可以得出: $$ z^{[1]} = W^{[1]}x+b^{[1]} $$ $$ a^{[1]} = g(z^{[1]}) = z^{[1]} $$ $$ z^{[2]} = W^{[2]} a^{[1]} + b^{[2]} = W^{[2]} (W^{[1]}x+b^{[1]}) + b^{[2]} $$ $$ a^{[2]} = g(z^{[2]}) = z^{[2]} = W^{[2]} (W^{[1]}x+b^{[1]}) + b^{[2]} = W^{[1]}W^{[2]} x + W^{[2]}b^{[1]} +b^{[2]} $$ $$ \hat{y} = a^{[2]} = W^{[1]}W^{[2]} x + W^{[2]}b^{[1]} +b^{[2]} $$ 可以看出,當激活函數為**線性激活函數**時,輸出 $ \hat{y} $ 不過是輸入特征 $ x $ 的**線性組合**(無論多少層),而不使用神經網絡也可以構建這樣的線性組合。而當激活函數為**非線性激活函數**時,通過神經網絡的不斷加深,可以構建出各種有趣的函數。
引用及參考:
[1] https://mooc.study.163.com/learn/2001281002?tid=2001392029#/learn/content?type=detail&id=2001702017
[2] https://blog.csdn.net/kangyi411/article/details/78969642
[3] https://blog.csdn.net/cherrylvlei/article/details/53149381
寫在最后:本文參考以上資料進行整合與總結,屬於原創,文章中可能出現理解不當的地方,若有所見解或異議可在下方評論,謝謝!
若需轉載請注明:https://www.cnblogs.com/lliuye/p/9486500.html
