github:代碼實現之神經網絡 本文算法均使用python3實現
1. 什么是神經網絡
人工神經網絡(artificial neural network,縮寫ANN),簡稱神經網絡(neural network,縮寫NN)或類神經網絡,是一種模仿生物神經網絡(動物的中樞神經系統,特別是大腦)的結構和功能的數學模型或計算模型,用於對函數進行估計或近似。 神經網絡主要由:輸入層,隱藏層,輸出層構成。當隱藏層只有一層時,該網絡為兩層神經網絡,由於輸入層未做任何變換,可以不看做單獨的一層。實際中,網絡輸入層的每個神經元代表了一個特征,輸出層個數代表了分類標簽的個數(在做二分類時,如果采用sigmoid分類器,輸出層的神經元個數為1個;如果采用softmax分類器,輸出層神經元個數為2個),而隱藏層層數以及隱藏層神經元是由人工設定。一個基本的三層神經網絡可見下圖:

1.1 從邏輯回歸到神經元
為了便於大家理解,我們先回顧一下邏輯回歸。邏輯回歸模型如下: \(h_\theta(x) = \frac{1}{1+e^{-\theta^T x}}\) 其中 \(z = \theta^T x = \theta_0 + \theta_1x_1 + \theta_2 x_2\) , \(h_\theta(x) = g(z) = \frac{1}{1+e^{-z}}\) 對此我們可以用以下結構進行理解:
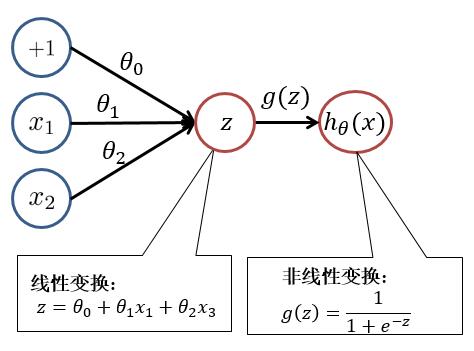
根據上圖,我們可以看出,邏輯回歸可以分為**線性變換**部分與**非線性變換**部分。而**只有輸入層與輸出層且輸出層只有一個神經元**的神經網絡的結構便於邏輯回歸一致。只不過在神經網絡中,**線性變換(求和)**與**非線性變換**被集成在一個神經元(隱藏層或輸出層)中。如下圖所示:
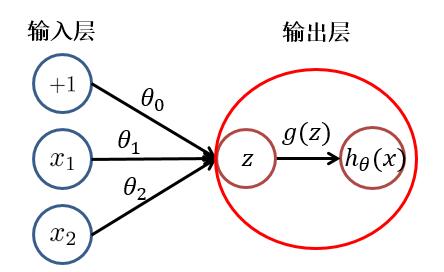
於是,對於具有多層或多個輸出神經元的神經網絡就不難理解了。其**每個**隱藏層**神經元**/輸出層**神經元**的值(**激活值**),都是由上一層神經元,經過**加權求和**與**非線性變換**而得到的。其中**非線性變換函數(又被稱為激活函數)**可以是: $ sigmoid、tanh、relu $ 等函數。
1.2 神經網絡
根據1.1中所講述,我們可以得到以下這樣一個基本的三層神經網絡:
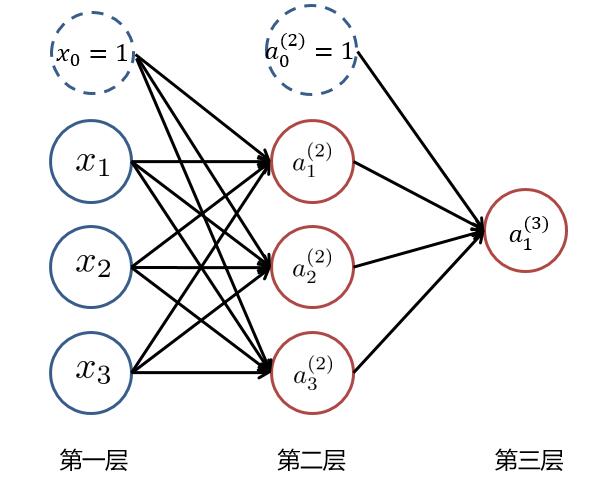
其中 $ x_i (i=1,2,3) $ 為輸入層的值,$ a_i^{(k)} (k=1,2,3...,K;i=1,2,3...,N_k) $ ,表示第 $ k $ 層中,第 $ i $ 個神經元的激活值, $ N_k $ 表示第 $ k $ 層的神經元個數。當 $ k=1 $ 時即為輸入層,即 $ a_i^{(1)} = x_i $ ,而 $ x_0 = 1 與 a_0^{(2)} =1 $ 為偏置項。 為了求最后的**輸出值 $ h_\theta(x)=a_1^{(3)} $**,我們需要計算隱藏層中每個神經元的激活值 $ a_{ji}^{(k)} (k=2,3) $。而隱藏層/輸出層的每一個神經元,都是由上一層神經元經過**類似邏輯回歸**計算而來。我們可以使用下圖進行理解:
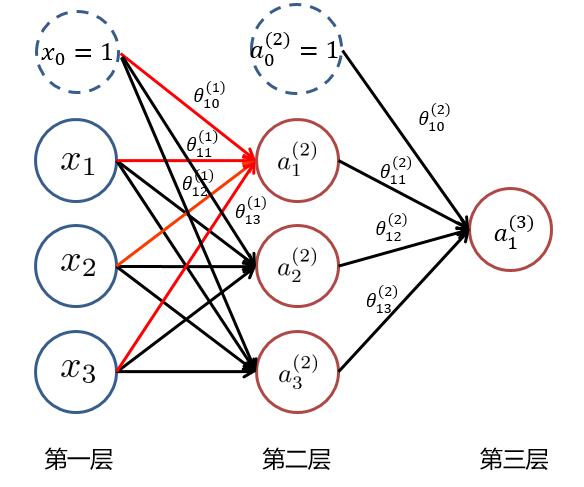
我們使用 $ \theta_{ji}^{(k)} $ 來表示第 $ k $ 層的參數(邊權),其中下標 $ j $ 表示第 $ k+1 $ 層的第 $ j $ 個神經元,$ i $ 表示第 $ k $ 層的第 $ i $ 個神經元。於是我們可以計算出**隱藏層**的三個**激活值**: $$ a_1^{(2)} = g(\theta_{10}^{(1)} x_0 + \theta_{11}^{(1)} x_1 + \theta_{12}^{(1)} x_2 +\theta_{13}^{(1)} x_3) $$ $$ a_2^{(2)} = g(\theta_{20}^{(1)} x_0 + \theta_{21}^{(1)} x_1 + \theta_{22}^{(1)} x_2 +\theta_{23}^{(1)} x_3) $$ $$ a_3^{(2)} = g(\theta_{30}^{(1)} x_0 + \theta_{31}^{(1)} x_1 + \theta_{32}^{(1)} x_2 +\theta_{33}^{(1)} x_3) $$ 再將隱藏層的三個激活值以及偏置項( $ a_0^{(2)},a_1^{(2)},a_2^{(2)},a_3^{(2)} $ )用來計算出輸出層神經元的**激活值**即為該神經網絡的輸出: $$ a_1^{(3)} = g(\theta_{10}^{(2)} a_0^{(2)} + \theta_{11}^{(2)} a_1^{(2)} + \theta_{12}^{(2)} a_2^{(2)} +\theta_{13}^{(2)} a_3^{(2)}) $$ 其中 $ g(z) $ 為**非線性變換函數(激活函數)**。 到此,我們就大致了解了什么是神經網絡了。
1.3 為什么要使用神經網絡
首先,神經網絡應用在分類問題中效果很好。 工業界中分類問題居多。LR或者linear SVM更適用線性分類。如果數據非線性可分(現實生活中多是非線性的),LR通常需要靠特征工程做特征映射,增加高斯項或者組合項;SVM需要選擇核。 而增加高斯項、組合項會產生很多沒有用的維度,增加計算量。GBDT可以使用弱的線性分類器組合成強分類器,但維度很高時效果可能並不好。而神經網絡在三層及以上時,能夠很好地進行非線性可分。現在我們使用下面的例子進行一下解釋。 有這樣一組樣本,如下圖:
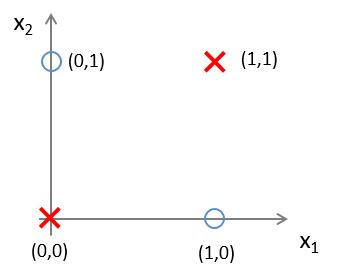

若我們需要對上圖中的樣本進行分類,直觀來看,**很難找到一條線性分類邊界對其進行分類**,而觀察上表中的輸入輸出值,我們可以看出分類結果與輸入值是**異或**關系。**而邏輯回歸可以通過改變參數,來實現“與”、“或”、“非”簡單操作**。 (1)我們先來觀察一下**邏輯回歸**實現**邏輯“與”操作**,假設模型函數如下: $$ h_\theta^{(1)}(x) = g(-30 + 20x_1+20x_2) = \frac{1}{1+e^{-(-30 + 20x_1+20x_2)}} $$ 對應結構與結果為:


(2)**邏輯回歸**實現**邏輯“或非”操作**,假設模型函數如下: $$ h_\theta^{(1)}(x) = g(-10 - 20x_1- 20x_2) = \frac{1}{1+e^{-(10 - 20x_1 - 20x_2)}} $$ 對應結果為:
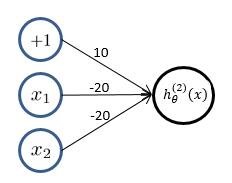

(3)**邏輯回歸**實現**邏輯“或”操作**,假設模型函數如下: $$ h_\theta^{(1)}(x) = g(-10 + 20x_1 + 20x_2) = \frac{1}{1+e^{-(10 + 20x_1 + 20x_2)}} $$ 對應結果為:
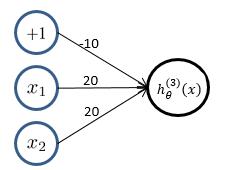

**觀察(1)(2)中的 $ h_\theta^{(1)}(x) 與 h_\theta^{(2)}(x) $ 的值,通過“或”操作,便能夠得到“異或”操作的結果。**
也就是說,若將三個**邏輯回歸**操作進行**疊加**,便能夠對上述例子進行**非線性分類**。大致結構圖可理解為下:
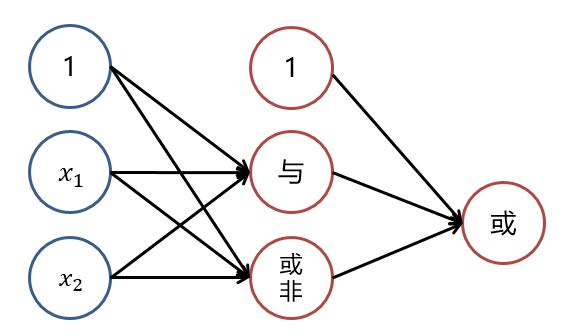

而對**線性分類器**的邏輯與和邏輯或的**組合**可以完美的對平面樣本進行分類。

隱層決定了最終的分類效果 :

由上圖可以看出,隨着隱層層數的增多,凸域將可以形成任意的形狀,因此可以解決任何復雜的分類問題。實際上,Kolmogorov理論指出:雙隱層感知器就足以解決任何復雜的分類問題。
於是我們可以得出這樣的結論:**神經網絡**通過將線性分類器進行組合疊加,能夠較好地進行**非線性分類**。
2.神經網絡目標函數
同樣的,對於神經網絡我們也需要知道其目標函數,才能夠對目標函數進行優化從而學習到參數。 假設神經網絡的輸出層只有一個神經元,該網絡有 \(K\) 層,則其目標函數為(若不止一個神經元,每個輸出神經元的目標函數類似,僅僅是參數矩陣的不同): \(J(\theta) = - \frac{1}{m} [ \sum_{i=1}^m y^{(i)} \log(h_\theta(a^{(K-1)})) + (1-y^{(i)}) \log(1-h_\theta(a^{(K-1)}))] + \frac{\lambda}{2m} \sum_{k=1}^{K-1} \sum_{i=1}^{N_k} \sum_{j=1}^{N_{k+1}} (\theta_{ji}^{(k)})^2\) 其中 \(a^{(i)}\) 倒數第2層的激活值,作為輸出層的輸入值。而其值為 \(a^{(k)} = g(a^{(k-1)})\) , \(y^{(i)}\) 為實際分類結果 \(0/1\) , \(m\) 為樣本數,\(N_k\) 為第 \(k\) 層的神經元個數。
3.神經網絡優化算法
神經網絡與普通的分類器不同,其是一個巨大的網絡,最后一層的輸出與每一層的神經元都有關系。而神經網絡的每一層,與下一層之間,都存在一個參數矩陣。我們需要通過優化算法求出每一層的參數矩陣,對於一個有 \(K\) 層的神經網絡,我們共需要求解出 \(K-1\) 個參數矩陣。因此我們無法直接對目標函數進行梯度的計算來求解參數矩陣。 對於神經網絡的優化算法,主要需要兩步:前向傳播(Forward Propagation)與反向傳播(Back Propagation)
3.1 前向傳播
前向傳播就是從輸入層到輸出層,計算每一層每一個神經元的激活值。也就是先隨機初始化每一層的參數矩陣,然后從輸入層開始,依次計算下一層每個神經元的激活值,一直到最后計算輸出層神經元的激活值。 以下面這個例子來看:
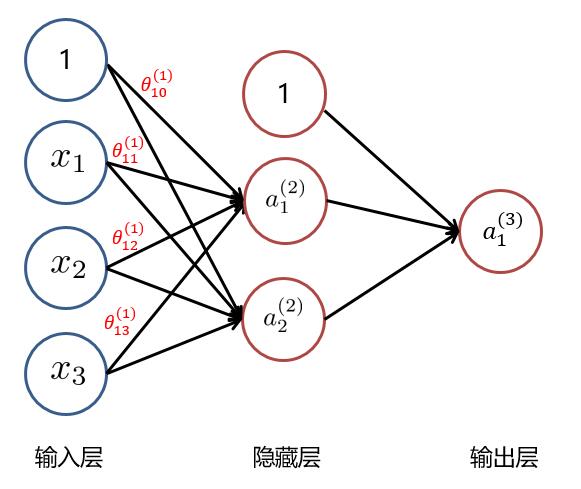
(1)隨機初始化參數矩陣 $ \Theta^{(1)} 與 \Theta^{(2)} $ : $$ \Theta^{(1)} = \begin{bmatrix} \theta_{10}^{(1)} & \theta_{11}^{(1)} & \theta_{12}^{(1)} & \theta_{13}^{(1)} \\ \theta_{20}^{(1)} & \theta_{21}^{(1)} & \theta_{22}^{(1)} & \theta_{23}^{(1)} \\ \end{bmatrix} \Theta^{(2)} = \begin{bmatrix} \theta_{10}^{(2)} & \theta_{11}^{(2)} & \theta_{12}^{(2)} \\ \end{bmatrix} $$ (2)計算隱藏層的每個神經元激活值: $$ a_1^{(2)} = g(\theta_{10}^{(1)} x_0 + \theta_{11}^{(1)} x_1 + \theta_{12}^{(1)} x_2 +\theta_{13}^{(1)} x_3) $$ $$ a_2^{(2)} = g(\theta_{20}^{(1)} x_0 + \theta_{21}^{(1)} x_1 + \theta_{22}^{(1)} x_2 +\theta_{23}^{(1)} x_3) $$ 即: $$ a^{(2)} = g(\Theta^{(1)} x) ,其中 a^{(2)} = \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \\ \end{bmatrix} , x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} $$ (3)計算隱藏層的每個神經元激活值: $$ a_1^{(3)} = g(\theta_{10}^{(2)} a_0^{(2)} + \theta_{11}^{(2)} a_1^{(2)} + \theta_{12}^{(2)} a_2^{(2)} ) $$ 即: $$ a^{(3)} = g(\Theta^{(2)} a^{(2)}) ,其中 a^{(2)} = \begin{bmatrix} a_0^{(2)} \\ a_1^{(2)} \\ a_2^{(2)} \\ \end{bmatrix} $$ 以上便是**前向傳播**計算**激活值**的過程。
3.2 反向傳播
反向傳播總的來說就是根據前向傳播計算出來的激活值,來計算每一層參數的梯度,並從后往前進行參數的更新。 在介紹反向傳播的計算步驟之前,我們先引入一個概念---除輸入層外每個神經元節點的**“損失”** ,\(\delta_j^{k}\) 表示第 \(k\) 層第 \(j\) 個神經元的損失。 於是我們可以計算求得(除輸入層)每一層神經元的損失(以上一個例子來解釋): \(\delta_1^{(3)} = a_1^{(3)} - y_1\) 其中 \(y_1\) 為實際值。向量化表示如下: \(\delta^{(3)} = a^{(3)} - y\) \(\delta^{(2)} = ((\Theta^{(2)})^T) \delta^{(3)} \cdot \ast g'(z^{(2)})\) 其中 \(\cdot \ast\) 表示兩個矩陣對應位置上元素相乘, \(g'(z^{(2)})\) 是對函數求導。而 $$ z^{(2)} = \begin \theta_{10}{(1)} x_0 + \theta_{11}{(1)} x_1 + \theta_{12}{(1)} x_2 +\theta_{13}{(1)} x_3 \ \theta_{20}{(1)} x_0 + \theta_{21}{(1)} x_1 + \theta_{22}{(1)} x_2 +\theta_{23}{(1)} x_3 \ \end$$ 由上可看出,第二層的損失 \(\delta^{(2)}\) 是基於第三層的損失 \(\delta^{(3)}\) 計算而來。也就是說,我們可以先計算第三層的損失並對第二層的參數矩陣進行更新,再利用第三層的損失計算第二層的損失以及更新第一層的參數矩陣(至於為何可以這樣進行,將在后面進行證明)。 於是,基於反向傳播算法的梯度更新步驟如下: (1)計算每一層的損失:\(\delta^{k}\)(見上面所示)。 (2)計算每一層的 \(\Delta\) (初始化為0):\(\Delta^{(k)} = \Delta^{(k)} + \delta^{(k+1)} (a^{(k)})^T\) (3)計算每一個參數的梯度: \(D_{ji}^{(k)} = \frac{1}{m} \Delta_{ji}^{(k)} + \lambda \Theta_{(ji)}^{(k)} , 如果 i \neq 0\) \(D_{ji}^{(k)} = \frac{1}{m} \Delta_{ji}^{(k)} , 如果 i = 0\) 也就是說 \(\frac{\delta J(\Theta)}{\delta \Theta_{ji}^{k}} = D_{ji}^{(k)}\)。於是就可以使用梯度下降來進行參數的求解了。
3.3 反向傳播的推導
大家可能都會有疑問,為什么求梯度時,要先對后一層進行計算,並利用其結果來求前一層的梯度?我們將針對如下例子進行推導證明:

第一層的參數為: $$ \Theta^{(1)} = \begin{bmatrix} \theta_{10}^{(1)} & \theta_{11}^{(1)} & \theta_{12}^{(1)} & \theta_{13}^{(1)} \\ \theta_{20}^{(1)} & \theta_{21}^{(1)} & \theta_{22}^{(1)} & \theta_{23}^{(1)} \\ \end{bmatrix} $$ 第二層的參數為: $$ \Theta^{(2)} = \begin{bmatrix} \theta_{10}^{(2)} & \theta_{11}^{(2)} & \theta_{12}^{(2)} \\ \end{bmatrix} $$ 我們先來對第二層的參數求梯度 $ \frac{\delta J(\Theta)}{\delta \theta^{(2)}} $ :

其中 $ y^i $ 為實際值, $ g(\theta^{(2)} a^{(2)}) = a^{(3)} $ 。

這一步的推導過程與邏輯回歸一樣,詳細可參考[邏輯回歸梯度求導過程](http://www.cnblogs.com/lliuye/p/9129493.html)。 現在我們來對第一層的參數求梯度 $ \frac{\delta J(\Theta)}{\delta \theta^{(1)}} $ :

先對中括號內的求導:
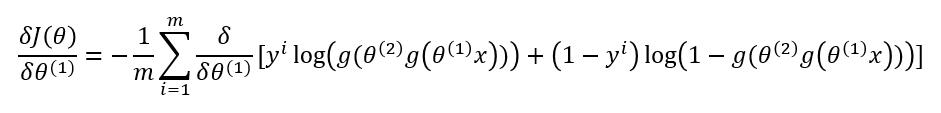

故:
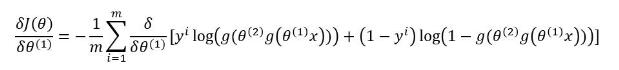 
對比着3.2中的公式,我們可以看出,第 $ k $ 層的梯度可以根據第 $ k+1 $ 層的**損失**來計算(上式是用第 $ 2 $ 的損失來推導第 $ 1 $ 層的梯度)。 到此,反向傳播的推導過程就完成了。如果對式子還有不理解的,可以自己動手多試試。
4.神經網絡算法分析
該部分參考博文[3] (1)理論上,單隱層神經網絡可以逼近任何連續函數(只要隱層的神經元個數足夠) (2)對於一些分類數據(比如CTR預估),3層神經網絡效果優於2層神經網絡,但如果把層數不斷增加(4,5,6層),對最后的結果的幫助沒有那么大的跳變。 (3)提升隱層數量或者隱層神經元個數,神經網絡的“容量”會變大,空間表達能力會變強。 (4)過多的隱層和神經元結點會帶來過擬合問題。 (5)不要試圖降低神經網絡參數量來減緩過擬合,用正則化或者dropout層。 注意:在代碼中對參數的初始化並不是使用0來初始化,還是在范圍 \([-\epsilon,\epsilon]\) 間隨機初始化。對應代碼為:
Theta = np.random.rand(nextUnit, Unit+1) * 2 * epsilon - epsilon
引用及參考: [1] 《Machine Learning》Andrew Ng [2] https://www.jianshu.com/p/a3b89d79f325 [3] https://blog.csdn.net/leiting_imecas/article/details/60463897 [4] https://blog.csdn.net/a819825294/article/details/53393837
寫在最后:本文參考以上資料進行整合與總結,屬於原創,文章中可能出現理解不當的地方,若有所見解或異議可在下方評論,謝謝! 若需轉載請注明:https://www.cnblogs.com/lliuye/p/9183914.html







