集成學習之Boosting —— AdaBoost原理

集成學習之Boosting —— AdaBoost原理

集成學習之Boosting —— AdaBoost實現

集成學習之Boosting —— Gradient Boosting原理

集成學習之Boosting —— Gradient Boosting實現

集成學習大致可分為兩大類：Bagging和Boosting。Bagging一般使用強學習器，其個體學習器之間不存在強依賴關系，容易並行。Boosting則使用弱分類器，其個體學習器之間存在強依賴關系，是一種序列化方法。Bagging主要關注降低方差，而Boosting主要關注降低偏差。Boosting是一族算法，其主要目標為將弱學習器“提升”為強學習器，大部分Boosting算法都是根據前一個學習器的訓練效果對樣本分布進行調整，再根據新的樣本分布訓練下一個學習器，如此迭代M次，最后將一系列弱學習器組合成一個強學習器。而這些Boosting算法的不同點則主要體現在每輪樣本分布的調整方式上。本系列文章先討論Boosting的兩大經典算法 —— AdaBoost和Gradient Boosting，再探討近年來在各大數據科學比賽中大放異彩的XGBoost和LightGBM。

AdaBoost原理概述

AdaBoost是一個具有里程碑意義的算法，因為其是第一個具有適應性的算法，即能適應弱學習器各自的訓練誤差率，這也是其名稱的由來（Ada為Adaptive的簡寫）。

AdaBoost的具體流程為先對每個樣本賦予相同的初始權重，每一輪學習器訓練過后都會根據其表現對每個樣本的權重進行調整，增加分錯樣本的權重，這樣先前做錯的樣本在后續就能得到更多關注，按這樣的過程重復訓練出M個學習器，最后進行加權組合，如下圖所示。

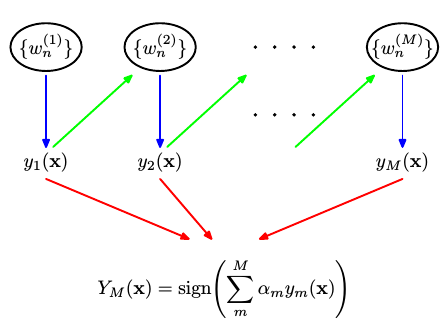
下圖顯示通過將簡單學習器加權組合就能生成具有復雜邊界的強學習器。

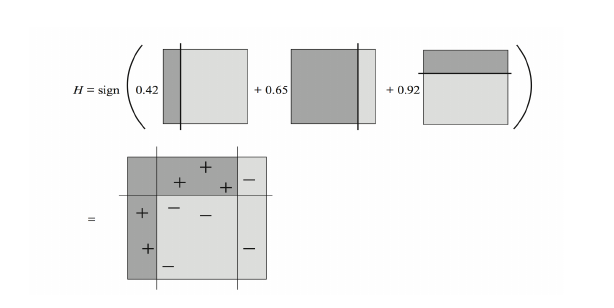
這里有兩個關鍵問題：

1. 每輪訓練過后如何調整樣本權重$w$？
2. 如何確定最后各學習器的權重 \(\alpha\) ？

這兩個問題可由加法模型和指數損失函數推導出來。

加法模型 (Additive Model) 和指數損失函數 (Exponential Loss)

由上圖可以看出，AdaBoost最后得到的強學習器是由一系列的弱學習器的線性組合，此即加法模型： $$ f(x) = \sum_^\alpha_G_(x)$$

其中$G_(x)\(為基學習器，\)\alpha_$為系數。

在第m步，我們的目標是最小化一個指定的損失函數$L(y,f(x))$，即

\[ \min\limits_{(\alpha_{m}\,,\,G_{m})}\sum\limits_{i=1}^{N}L(y_{i}, \,\sum\limits_{m=1}^{M}\alpha_{m}G_{m}(x_{i})) \tag{1.1} \]

其中 $(x_{1},y_{1}),(x_{2},y_{2}),\cdots(x_,y_)$為訓練數據集。

這是個復雜的全局優化問題，通常我們使用其簡化版，即假設在第m次迭代中，前m-1次的系數$\alpha$和基學習器$G(x)$都是固定的，則$f_(x) = f_(x) + \alpha_G_(x)\(，這樣在第m步我們只需就當前的\)\alpha_$和$G_(x)$最小化損失函數。

AdaBoost采用的損失函數為指數損失，形式如下：

\[ L(y,\,f(x)) = e^{-yf(x)} \tag{1.2} \]

結合上文，我們現在的目標是在指數函數最小的情況下求得$\alpha_$和$G_(x)$。

\[ (\alpha_{m},G_{m}(x)) = \mathop{\arg\min}\limits_{(\alpha,G)}\sum\limits_{i=1}^{N}e^{-y_{i}f_{m}(x_{i})} = \mathop{\arg\min}\limits_{(\alpha,G)}\sum\limits_{i=1}^{N}e^{-y_{i}(f_{m-1}(x_{i}) + \alpha G(x_{i}))} \tag{1.3} \]

設 \(w_{i}^{(m)} = e^{-y_{i}f_{m-1}(x_{i})}\)，由於$w_i^{(m)}\(不依賴於\)\alpha$和$G(x)$，所以可認為其是第m步訓練之前賦予每個樣本的權重。然而$w_i^{(m)}$依賴於$f_(x_i)$，所以每一輪迭代會改變。
於是式 (1.3) 變為：

\[ \sum\limits_{i=1}^{N}w_{i}^{(m)}e^{-y_i\alpha G(x_i)} = e^{-\alpha}\sum\limits_{y_{i}=G(x_{i})}w_{i}^{(m)} + e^{\alpha}\sum\limits_{y_i \neq G(x_i)}w_i^{(m)} \tag{1.4} \]

\[ = (e^{\alpha} - e^{-\alpha})\sum\limits_{i=1}^Nw_i^{(m)}\mathbb{I}(y_i \neq G(x_i)) + e^{-\alpha}\sum\limits_{i=1}^Nw_i^{(m)} \tag{1.5} \]

由上面幾個式子可以得到AdaBoost算法的幾個關鍵點：

(1) 基學習器$G_m(x)$ :

求令式 (1.5) 最小的$G_m(x)$等價於令 \(\sum\limits_{i=1}^Nw_i^{(m)}\mathbb{I}(y_i \neq G(x_i))\) 最小化的$G_m(x)$，因此可認為每一輪基學習器都是通過最小化帶權重誤差得到。

(2) 下一輪樣本權值$w_i^{(m+1)}$ ：

由 \(w_{i}^{(m+1)} = e^{-y_{i}f_{m}(x_{i})} = e^{-y_{i}(f_{m-1}(x_{i}) + \alpha G(x_{i}))} = e^{-y_if_{m-1}(x_i)}e^{-y_i\alpha_mG_m(x_i)} = w_i^{(m)}e^{-y_i\alpha_mG_m(x_i)}\)

可以看到對於$\alpha_m>0$，若$y_i = G_m(x_i)$，則$w_i^{(m+1)} = w_i^{(m)}e^{-\alpha_m}$，表明前一輪被正確分類樣本的權值會減小； 若$y_i \neq G_m(x_i)$，則$w_i^{(m+1)} = w_i^{(m)}e^{\alpha_m}$，表明前一輪誤分類樣本的權值會增大。

(3) 各基學習器的系數 \(\alpha_m\) ：

設$G_m(x)$在訓練集上的帶權誤差率為 \(\epsilon_m = \frac{\sum\limits_{i=1}^Nw_i^{(m)}\mathbb{I}(y_i \neq G_m(x_i))}{\sum\limits_{i=1}^Nw_i^{(m)}}\) ，

式 (1.4) 對$\alpha$ 求導並使導數為0： \(-e^{-\alpha}\sum\limits_{y_{i}=G(x_{i})}w_{i}^{(m)} + e^{\alpha}\sum\limits_{y_i \neq G(x_i)}w_i^{(m)} = 0\) ，

兩邊同乘以$e^\alpha$，得 \(e^{2\alpha} = \frac{\sum\limits_{y_{i}=G(x_{i})}w_{i}^{(m)}}{\sum\limits_{y_{i} \neq G(x_{i})}w_{i}^{(m)}} = \frac{1-\epsilon_m}{\epsilon_m}\) \(\quad {\color{Red}{\Longrightarrow}} \quad\) \(\alpha_m = \frac{1}{2}ln\frac{1-\epsilon_m}{\epsilon_m}\)

可以看出，$\epsilon_m​$越小，最后得到的$\alpha_m​$就越大，表明在最后的線性組合中，准確率越高的基學習器會被賦予較大的系數。

AdaBoost算法

在了解了$G_m(x)$，$w_i^{(m+1)}\(和\)\alpha_m$的由來后，AdaBoost算法的整體流程也就呼之欲出了：

輸入： 訓練數據集 \(T = \left \{(x_1,y_1), (x_2,y_2), \cdots (x_N,y_N)\right \}\)，\(y\in\left\{-1,+1 \right\}\)，基學習器$G_m(x)$，訓練輪數M

1. 初始化權值分布： \(w_i^{(1)} = \frac{1}{N}\:, \;\;\;\; i=1,2,3, \cdots N\)
2. for m=1 to M: (a) 使用帶有權值分布的訓練集學習得到基學習器$G_m(x)$: \(G_m(x) = \mathop{\arg\min}\limits_{G(x)}\sum\limits_{i=1}^Nw_i^{(m)}\mathbb{I}(y_i \neq G(x_i))\) \(\qquad\) (b) 計算$G_m(x)$在訓練集上的誤差率： \(\epsilon_m = \frac{\sum\limits_{i=1}^Nw_i^{(m)}\mathbb{I}(y_i \neq G_m(x_i))}{\sum\limits_{i=1}^Nw_i^{(m)}}\) \(\qquad\)(c) 計算$G_m(x)$的系數： \(\alpha_m = \frac{1}{2}ln\frac{1-\epsilon_m}{\epsilon_m}\) \(\qquad\)(d) 更新樣本權重分布： \(w_{i}^{(m+1)} = \frac{w_i^{(m)}e^{-y_i\alpha_mG_m(x_i)}}{Z^{(m)}}\; ,\qquad i=1,2,3\cdots N\) 　　其中$Z^{(m)}$是規范化因子，\(Z^{(m)} = \sum\limits_{i=1}^Nw^{(m)}_ie^{-y_i\alpha_mG_m(x_i)}\)，以確保所有的$w_i^{(m+1)}$構成一個分布。
3. 輸出最終模型： \(G(x) = sign\left[\sum\limits_{m=1}^M\alpha_mG_m(x) \right]\)

AdaBoost采用指數損失的原因

若將指數損失表示為期望值的形式：

\[ E(e^{-yf(x)}|x) = P(y=1|x)e^{-f(x)} + P(y=-1|x)e^{f(x)} \]

由於是最小化指數損失，則將上式求導並令其為0：

\[ \frac{\partial E(e^{-yf(x)}|x)}{\partial f(x)} = -P(y=1|x) e^{-f(x)} + P(y=-1|x)e^{f(x)} = 0\quad ， \]

\[ f(x) = \frac12 log\frac{P(y=1|x)}{P(y=-1|x)}，或寫為 P(y=1|x) = \frac{1}{1+e^{-2f(x)}} \]

仔細看，這不就是logistic regression嗎？二者只差系數$\frac12$，因此每一輪最小化指數損失其實就是在訓練一個logistic regression模型，以逼近對數幾率 (log odds)。

於是，

\[ \begin{equation} \begin{aligned} \text{sign}(f(x)) &= \text{sign}(\frac12 log\frac{P(y=1|x)}{P(y=-1|x)}) \\ & =\left\{\begin{matrix} 1 & \;\; P(y=1|x) > p(y=-1|x)\\ -1 & \;\; P(y=1|x) < P(y=-1|x) \end{matrix}\right. \\&=\mathop{\arg\max} \limits_{y \in\{-1,1\}}P(y|x) \end{aligned} \end{equation} \]

這意味着$\text(f(x))$達到了貝葉斯最優錯誤率，即對於每個樣本$x$都選擇后驗概率最大的類別。若指數損失最小化，則分類錯誤率也將最小化。這說明指數損失函數是分類任務原本0-1損失函數的一致性替代函數。由於這個替代函數是單調連續可微函數，因此用它代替0-1損失函數作為優化目標。

##Real AdaBoost

上文推導出的AdaBoost算法被稱為"Discrete AdaBoost"，因為其各個基學習器$G_m(x)$的輸出為{-1,1} 。如果將基學習器的輸出改為一個類別概率，則產生了Real AdaBoost。Real AdaBoost通常在更少的輪數達到更高的精度，像scikit-learn中的AdaBoostClassifier就是默認優先使用Real AdaBoost (SAMME.R)，不過Real AdaBoost中的基學習器必須支持概率估計。

推導與Discrete AdaBoost類似，仍最小化指數損失：

\(\begin{equation} \begin{aligned} E(e^{-yf_m(x)}|x) &= E(e^{-y(f_{m-1}(x) + G(x))}|x) \\ &=E(w \cdot e^{-yG(x)}|x) \\&=e^{-G(x)}P_w(y=1|x) + e^{G(x)}P_w(y=-1|x)\end{aligned} \end{equation}\)
對 \(G(x)\) 求導： \(G(x) = \frac12log\frac{P_w(y=1|x)}{P_w(y=-1|x)}\)

其中$P_w(y=1|x)$是權重為$w$下y=1的概率，注意這里的$G(x)$不是基學習器，而是基學習器的類別概率的一個對數轉換。由此Real AdaBoost的算法流程如下：

1. 初始化權重分布：\(w_i^{(1)} = \frac1N, \qquad i = 1,2 \cdots N\)
2. for m=1 to M: 　　(a) 使用帶權重分布的訓練集訓練基學習器，得到類別概率$P_m(x) = P_w(y=1|x) ;\in [0,1]$ 　　(b) \(G_m(x) = \frac12 log\frac{P_m(x)}{1-P_m(x)} \;\in R\) 　　(c) 更新權重分布： \(w_i^{(m+1)} = \frac{w_i^{(m)}e^{-y_iG_m(x_i)}}{Z^{(m)}}\)
3. 輸出最終模型：\(G(x) = sign\left[\sum\limits_{m=1}^MG_m(x)\right]\)

正則化 (Regularization) 和其他

1、Shrinkage

對每個基學習器乘以一個系數$\nu$ (0 < \(\nu\) <1)，使其對最終模型的貢獻減小，從而防止學的太快產生過擬合。$\nu$又稱學習率，即scikit-learn中的 learning rate。於是上文的加法模型就從：

​ \(f_m(x) = f_{m-1}(x) + \alpha_m G_m(x)\)

變為：

​ \(f_m(x) = f_{m-1}(x) + \nu \cdot \alpha_m G_m(x)\)

一般$\nu$要和迭代次數M結合起來使用，較小的$\nu$意味着需要較大的M。ESL中提到的策略是先將$\nu$設得很小 (\(\nu\) < 0.1)，再通過early stopping選擇M，不過現實中也常用cross-validation進行選擇。

2、Early stopping

將數據集划分為訓練集和測試集，在訓練過程中不斷檢查在測試集上的表現，如果測試集上的准確率下降到一定閾值之下，則停止訓練，選用當前的迭代次數M，這同樣是防止過擬合的手段。

3、Weight Trimming

weight trimming不是正則化的方法，其主要目的是提高訓練速度。在AdaBoost的每一輪基學習器訓練過程中，只有小部分樣本的權重較大，因而能產生較大的影響，而其他大部分權重小的樣本則對訓練影響甚微。Weight trimming的思想是每一輪迭代中刪除那些低權重的樣本，只用高權重樣本進行訓練。具體是設定一個閾值 (比如90%或99%)，再將所有樣本按權重排序，計算權重的累積和，累積和大於閾值的權重 (樣本) 被舍棄，不會用於訓練。注意每一輪訓練完成后所有樣本的權重依然會被重新計算，這意味着之前被舍棄的樣本在之后的迭代中如果權重增加，可能會重新用於訓練。

根據 [Friedman et al., 2000] 中的描述，weighting trimming可以提高計算效率，且不會犧牲准確率，下一篇中將通過實現來驗證。

終末

AdaBoost的原始論文 [Freund & Schapire, 1997] 並非使用了上文中的推導方法，而是基於PAC學習框架下進行解釋的。上文的將AdaBoost視為 “加法模型 + 指數損失” 的觀點，由斯坦福的幾位統計系大牛 [Friedman et al., 2000] 提出，因而這一派也被稱為“統計視角”。沿着這個路子，若將指數損失替換為其他損失函數並依此不斷訓練新學習器，則誕生了Gradient Boosting算法，是為下一篇的主題。

---

Reference :

1. Friedman, J., Hastie, T. and Tibshirani, R. Additive logistic regression: a statistical view of boosting
2. Friedman, J., Hastie, T. and Tibshirani, R. The Elements of Staistical Learning
3. 周志華. 《機器學習》
4. 李航. 《統計學習方法》
5. Schapire R. E. Expalining AdaBoost

/