皮爾遜相關系數理解有兩個角度
其一, 按照高中數學水平來理解, 它很簡單, 可以看做將兩組數據首先做Z分數處理之后, 然后兩組數據的乘積和除以樣本數
Z分數一般代表正態分布中, 數據偏離中心點的距離.等於變量減掉平均數再除以標准差.(就是高考的標准分類似的處理)
標准差則等於變量減掉平均數的平方和,再除以樣本數,最后再開方.
所以, 根據這個最朴素的理解,我們可以將公式依次精簡為:
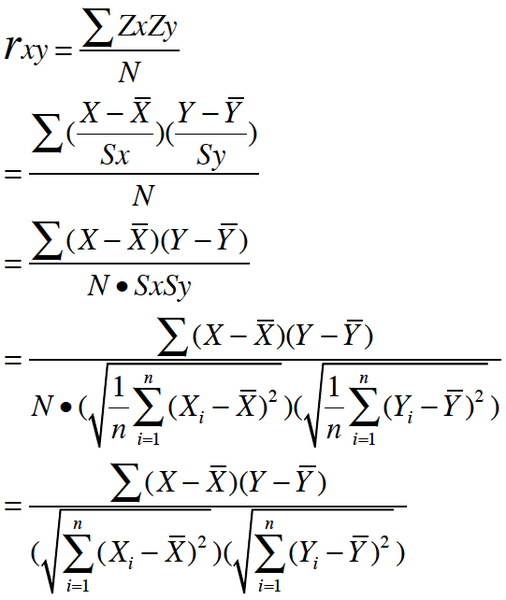
其二, 按照大學的線性數學水平來理解, 它比較復雜一點,可以看做是兩組數據的向量夾角的余弦.
皮爾遜相關的約束條件
從以上解釋, 也可以理解皮爾遜相關的約束條件:
- 1 兩個變量間有線性關系
- 2 變量是連續變量
- 3 變量均符合正態分布,且二元分布也符合正態分布
- 4 兩變量獨立
在實踐統計中,一般只輸出兩個系數,一個是相關系數,也就是計算出來的相關系數大小,在-1到1之間;另一個是獨立樣本檢驗系數,用來檢驗樣本一致性.
先舉個手算的例子
使用維基中的例子:
例如,假設五個國家的國民生產總值分別是1、2、3、5、8(單位10億美元),又假設這五個國家的貧困比例分別是11%、12%、13%、15%、18%。
創建2個向量.(R語言)
x<-c(1,2,3,5,8)
y<-c(0.11,0.12,0.13,0.15,0.18)
按照維基的例子,應計算出相關系數為1出來.我們看看如何一步一步計算出來的.
x的平均數是:3.8
y的平均數是0.138
所以,
sum((x-mean(x))*(y-mean(y)))=0.308
用大白話來寫就是:
(1-3.8)*(0.11-0.138)=0.0784
(2-3.8)*(0.12-0.138)=0.0324
(3-3.8)*(0.13-0.138)=0.0064
(5-3.8)*(0.15-0.138)=0.0144
(8-3.8)*(0.18-0.138)=0.1764
0.0784+0.0324+0.0064+0.0144+0.1764=0.308
同理, 分號下面的,分別是:
sum((x-mean(x))^2)=30.8
sum((y-mean(y))^2)= 0.00308
用大白話來寫,分別是:
(1-3.8)^2=7.84 #平方
(2-3.8)^2=3.24 #平方
(3-3.8)^2=0.64 #平方
(5-3.8)^2=1.44 #平方
(8-3.8)^2=17.64 #平方
7.84+3.24+0.64+1.44+17.64=30.8
同理,求得:
sum((y-mean(y))^2)= 0.00308
然后再開平方根,分別是:
30.8^0.5=5.549775
0.00308^0.5=0.05549775
用分子除以分母,就計算出最終結果:
0.308/(5.549775*0.05549775)=1
- 再舉個簡單的R語言例子(R在這里下載: http://cran.r-project.org/bin/macosx/)
假設有100人, 一組數據是年齡,平均年齡是35歲,標准差是5歲;另一組數據是發帖數量,平均帖子數量是45份post,標准差是8份帖子.
假設這兩組都是正態分布.我們來求這兩者的皮爾遜相關系數,R腳本如下:
> x<-rnorm(n=100,mean=35,sd=5) #創建一組平均數為35,標准差為5,樣本數為100的隨機數 > y<-rnorm(n=100,mean=45,sd=8) #創建一組平均數為45,標准差為8,樣本數為100的隨機數 > cor.test(x,y,method="pearson") #計算這兩組數的相關,並進行T檢驗
然后R輸出結果為:
Pearson's product-moment correlation data: x and y t = -0.0269, df = 98, p-value = 0.9786 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.1990316 0.1938019 sample estimates: cor -0.002719791
當然,這里是隨機數.也可以用非隨機的驗證一下計算.
皮爾遜相關系數用於網站開發
直接將R與Ruby關聯起來
調用很簡單,仿照上述例子:
cor(x,y)
就輸出系數結果了.
有這么幾個庫可以參考:
https://github.com/alexgutteridge/rsr...
https://github.com/davidrichards/stat...
https://github.com/jtprince/simpler
說明, 以上為ruby調用庫. pythone程序員可以參考: Rpy (http://rpy.sourceforge.net/)
簡單的相關系數的分類
- 0.8-1.0 極強相關
- 0.6-0.8 強相關
- 0.4-0.6 中等程度相關
- 0.2-0.4 弱相關
- 0.0-0.2 極弱相關或無相關
ps : 這個網站開發者不要再次發明輪子,本來用markdown語法寫作很爽,結果又不得不花時間來改動.請考慮盡快支持Markdown語法.
